中考数学二轮复习课件 “一线三等角”模型的探究与应用

这是一份中考数学二轮复习课件 “一线三等角”模型的探究与应用，共16页。PPT课件主要包含了同侧型，异侧型，火眼金睛找K形，求BP，求EC，-2x4-x，以不变应万变，今天你学会了什么，小结与反思等内容，欢迎下载使用。
如图，在△ACD中，∠ACD=90°，AC=DC，按如下步骤操作：
（2）分别过点A、D作直线l的垂线段，垂足分别为点B、E；
从这个图形中你能得到什么结论？
结论：△ABC≌△CED
如果将△ACD的形状作一下改变，这个结论还成立吗？
“一线三直角”全等模型
探究1：若将等腰直角△ACD改为任意直角三角形，按上面的步骤(1)(2)作图；
结论：△ABC∽△CED
“一线三直角”基本图形
特征：∠ABC=∠ACD=∠CED=90°且顶点在同一直线上.
探究2：如图，若将直角三角形ACD改成任意△ACD，已知∠B=∠ACD=∠E=a，△ABC与△CDE还相似吗？请说明理由.
∴∠BAC+∠ACB=∠ACB+∠DCE=180°-a
“一线三等角”基本图形
特征：∠B=∠ACD=∠E=a且顶点在同一直线上
“一线三直角”相似模型
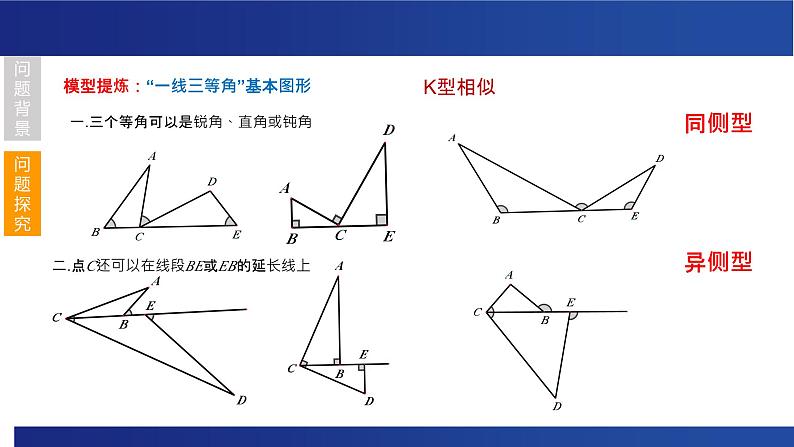
模型提炼：“一线三等角”基本图形
一.三个等角可以是锐角、直角或钝角
二.点C还可以在线段BE或EB的延长线上
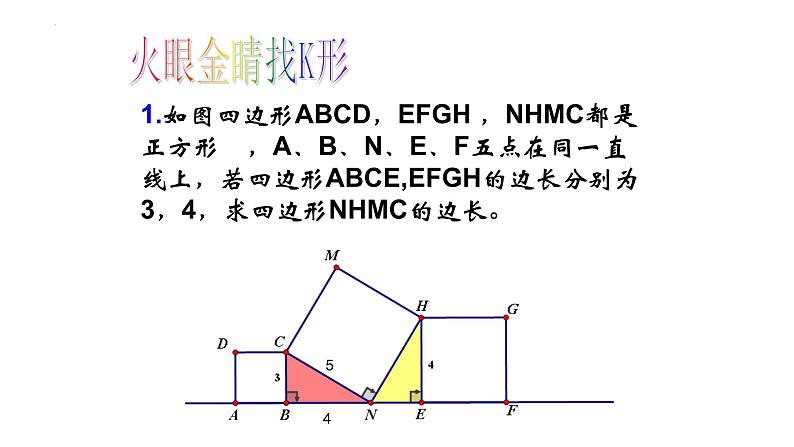
1.如图四边形ABCD，EFGH ，NHMC都是正方形 ，A、B、N、E、F五点在同一直线上，若四边形ABCE,EFGH的边长分别为3，4，求四边形NHMC的边长。
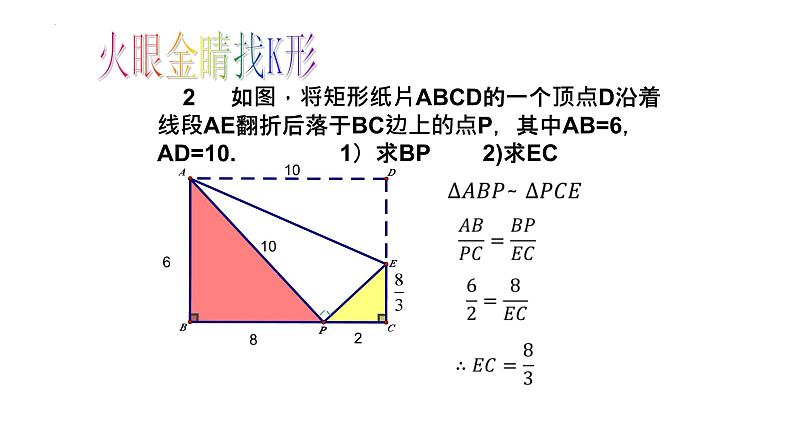
2 如图，将矩形纸片ABCD的一个顶点D沿着线段AE翻折后落于BC边上的点P，其中AB=6，AD=10.
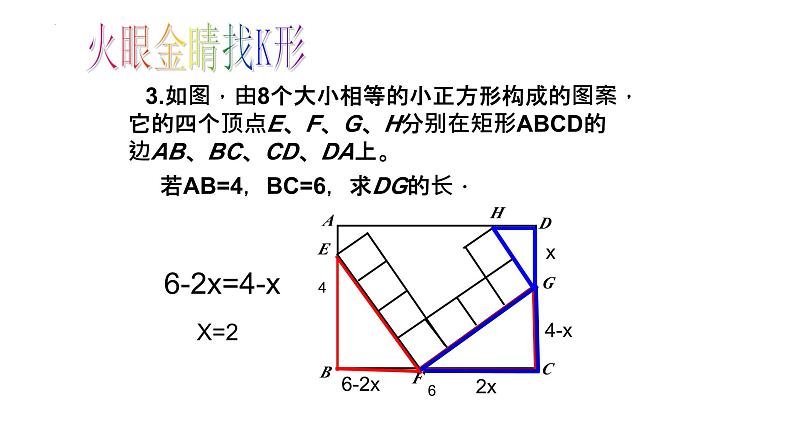
3.如图，由8个大小相等的小正方形构成的图案，它的四个顶点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上。
若AB=4，BC=6，求DG的长．
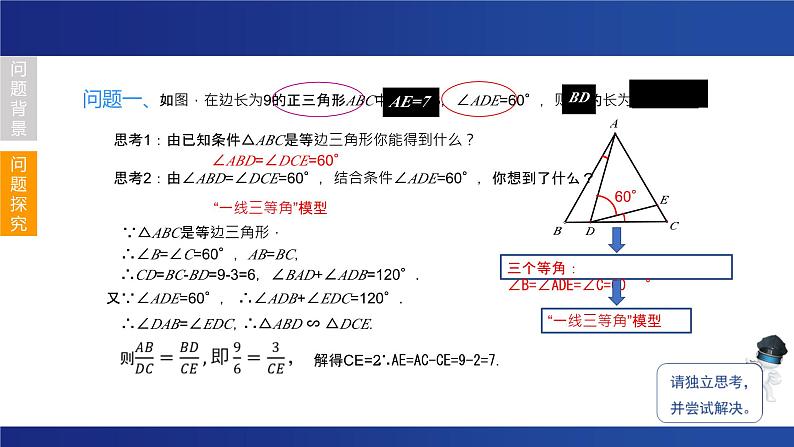
如图，在边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AE的长为________.
思考1：由已知条件△ABC是等边三角形你能得到什么？
∠ABD=∠DCE=60°
思考2：由∠ABD=∠DCE=60°，结合条件∠ADE=60°，你想到了什么？
∵△ABC是等边三角形，
∴CD=BC-BD=9-3=6，∠BAD+∠ADB=120°.
又∵∠ADE=60°，
∴∠DAB=∠EDC，
∴∠B=∠C=60°，AB=BC，
∴AE=AC-CE=9-2=7.
∴∠ADB+∠EDC=120°.
∴△ABD ∽ △DCE.
三个等角：∠B=∠ADE=∠C=60°
问题二、 如图，在平面直角坐标系xy中，直线y=-x+m分别交x轴，y轴于A，B两点，已知点C(2,0)，点P为线段OB的中点，连接PA，PC，若∠CPA=∠ABO，则m的值为___________.
思考1：由直线y=-x+m你能得到什么？
OB=OA=m，∠OBA=∠OAB=45°
思考2：结合条件∠CPA=∠ABO=45°你想到了什么？
找可能的另一“等角”构“一线三等角”
思考3：如将y轴看成“一线”，如何寻另一“等角”？
由y=-x+m可得A（m，0），B（0，m），
∵∠CPA=∠ABO=45°
又∵∠ABP=∠PDC=45°
∴∠BPA+∠OPC=∠BPA+∠BAP=135°
∴∠OPC=∠BAP .
问题三、已知：如图，在四边形ABCD中，AB=10，BF=4，∠B=60°，设AE=x,AG=y，求y与x的函数关系式.
问题四、（1）已知点A、B分别在反比例函数y= （x＞0），y= （x＞0）的图象上，且∠AOB=90°，则∠B=30°，则k的值为　　．
问题四、（2）如图，反比例函数 过A,B两点，若B (2，4) , OB ⊥AB 求点A的坐标；
问题五、如图，正方形的边长为6，P为BC边上的动点，连接AP，作 交CD边于点Q， 小明在写作业时，不小心将几滴黑墨水滴在题目上，看不清后面的问题 聪明的同学你能帮帮小明吗？（可以适当添加条件）