“隐形圆”点到圆最值问题-中考数学一轮复习课件

这是一份“隐形圆”点到圆最值问题-中考数学一轮复习课件，共16页。PPT课件主要包含了引入定理，探究定理，应用定理，课堂检测，课堂小结等内容，欢迎下载使用。

不积洼步 无以至千里。
隐形圆的应用是中考中的常见题目，这类题目在条件中没有直接给出有关圆的信息，但我们通过分析和转化，最终都可以利用圆的知识求解。这类题目构思巧妙，综合性强，它将复杂的问题转化为圆内的求角问题，体现了转化和化归的数学思想，处理这类题目，关键在于能否把“隐形圆”找出来。
平面内一定点D和圆O上动点E的连线中，当连线过圆心O时，线段DE有最大值和最小值．具体分以下三种情况讨论(规定：OD＝d，圆O半径为r)：1、 当D点在圆O外时，d >r，如图①、②：当D、E、O三点共线时，线段DE出现最值，DE的最大值为d＋r，DE的最小值为d－r；
分析：当D、E、O三点共线时，线段DE出现最值。理由，当三点不共线时，构成三角形，依据三角形三边关系，可证
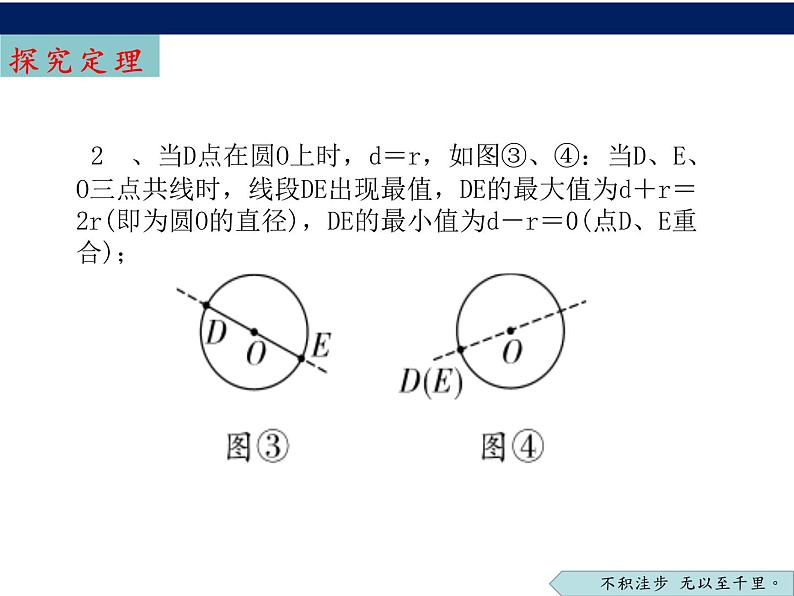
2 、当D点在圆O上时，d＝r，如图③、④：当D、E、O三点共线时，线段DE出现最值，DE的最大值为d＋r＝2r(即为圆O的直径)，DE的最小值为d－r＝0(点D、E重合)；
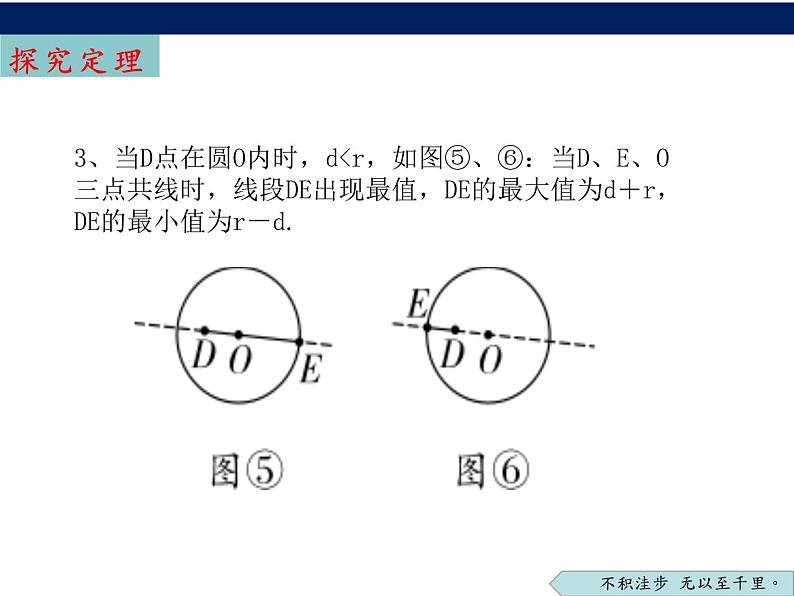
3、当D点在圆O内时，d例1如图，E、F是正方形ABCD的边AD上的两个动点，满足AE=DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是________．　
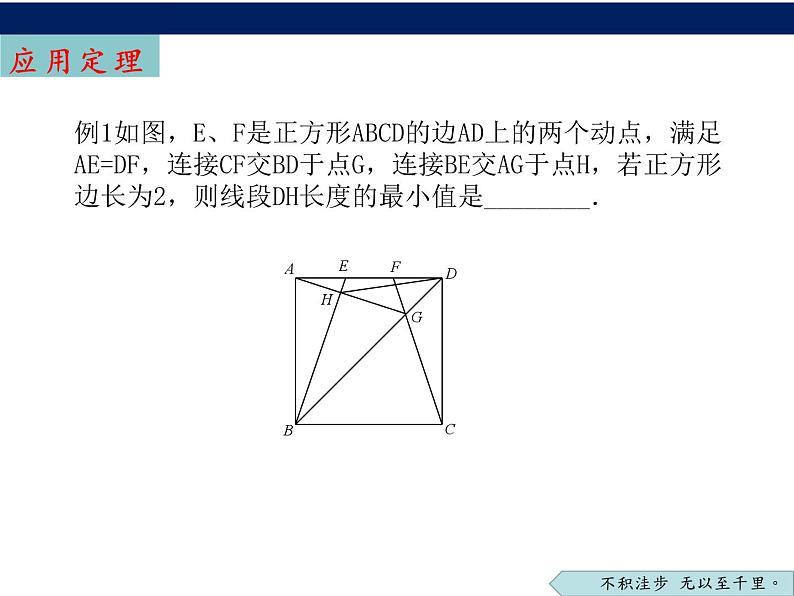
证明：在正方形ABCD中，AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，在△ABE和△DCF中，AB＝CD∠BAD＝∠CDA＝90°AE＝DF∴△ABE≌△DCF（SAS），∴∠1=∠2，在△ADG和△CDG中，AD＝CD∠ADG＝∠CDG＝45°DG＝DG∴△ADG≌△CDG（SAS），∴∠2=∠3，∴∠1=∠3，∵∠BAH+∠3=∠BAD=90°，∴∠1+∠BAH=90°，∴∠AHB=180°-90°=90°，∴BE⊥AG；∴∠AHB=90°
取AB的中点O为圆心画弧即：点H在弧AB上∴DH的最小值为d－r∵正方形的边长为2，OA=1=r∴d=∴DH长度的最小值
例2.某城市街角有一草坪，草坪是由草地和弦与其所对的劣弧围成的草地组成，如图所示．管理员王师傅在M处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水．于是，他主喷灌龙头的转角正好等于(即每次喷灌时喷灌龙头由转到，然后再转回，这样往复喷灌)，同时，再合理设计好喷灌龙头喷水的射程就可以了．如图，已测出，MB=10m AB=24m,∆ABM的面积为96m²;过弦AB的中点D作DE⊥AB交弧AB于点E，又测得DE=8m．请你根据以上提供的信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法?为什么?
解：作射线ED交AM于点C∵AD=DB,ED⊥AB,弧AB为劣弧 DE=8m AB=24m∴弧AB所在圆心在射线DC上假设圆心为O，半径为r,连接OA,则r²=12²+（r-8）²解得r=13∴OD=5过点M作MN⊥AB,垂足为N∵S∆ABM=96.AB=24∴MN=8,NB=6,AN=18∵∆ADC∽∆ANM∴∴DC= OD 例3.所示，AB、AC、BC是某新区的三条规划路其中，AB＝6km，AC＝3km，∠BAC＝60°，BC所对的圆心角为60°．新区管委会想在BC路边建物资总站点P，在AB、AC路边分别建物资分站点E、F．也就是，分别在BC线段AB和AC上选取点P、E、F．由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷环保和节约成本要使得线段PE、EF、FP之和最短，试求PE＋EF＋FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计)．
解：假设P点即为所求点，分别作出点P关于AB、AC的对称点P´、P＂连接PP´、P´E，PE，P＂F，PF，PP＂由对称性可知PE＋EF＋FP＝P´E＋EF＋FP＂＝P´P＂，当P´、E、F、P＂在一条直线上，P´P＂即为最短距离， ∵∆AP´P＂是120°等腰三角形，P´P＂= AP∴当PA最小时P´P＂也最小∵点A在圆外，PA最短=d－r∴作出弧BC的圆心O，连接AO，与弧BC交于P，∵AB＝6km，AC＝3km，∠BAC＝60°，∴∆ABC是直角三角形，∠ABC＝30°，BC＝ BC所对的圆心角为60°， ∴∆OBC是等边三角形，∠CBO＝60°，BO＝BC＝∴∠ABO＝90°，AO＝ ，PA＝ - ∠P´AE＝∠EAP，∠PAF＝∠FAP＂，∴∠P´AP＂＝2∠ABC＝120°，P´A＝AP＂，∴∠AP´E＝∠AP＂F＝30°∵P´P＂＝ P´A＝ －9所以PE＋EF＋FP的最小值为（ －9）km．
1.已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE=CF，连接AE、BF，交点为P点，则PD的最小值为_________
2.如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值是_________．
3.如图，在墙角放置一个“T”型钢尺，已知钢尺的一边AB＝10，M是AB的中点，CM＝8，AB沿墙壁边向下滑动，在运动过程中，点C到点O的最大距离为________．
同学们，分享你的收获！说说你的疑问？