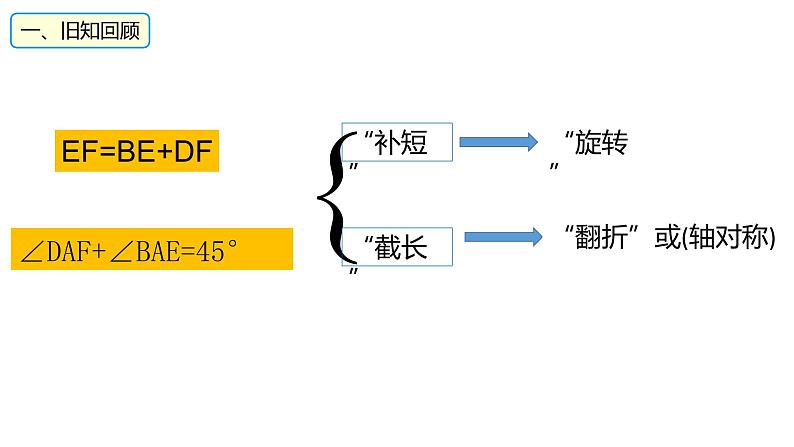
中考数学专题 第2课时 正方形之“半角”模型 课件

这是一份中考数学专题 第2课时 正方形之“半角”模型 课件，共17页。PPT课件主要包含了“补短”，EFBE+DF，“旋转”，“翻折”或轴对称，“截长”，求证AG⊥EG，求证AH⊥FH等内容，欢迎下载使用。
∠DAF+∠BAE=45°
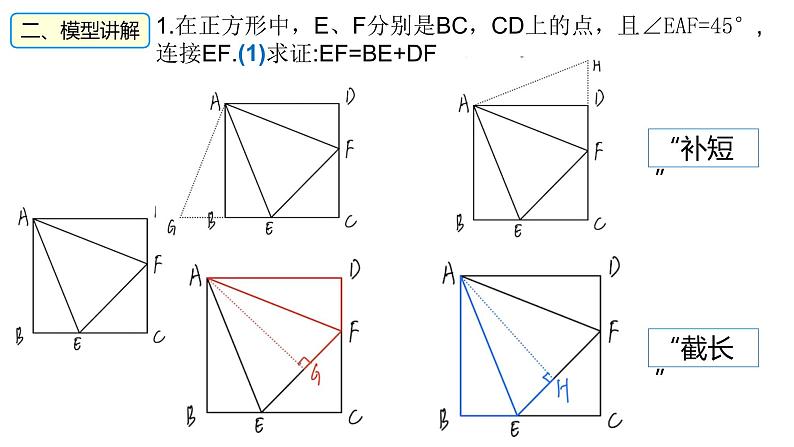
1.在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(1)求证:EF=BE+DF
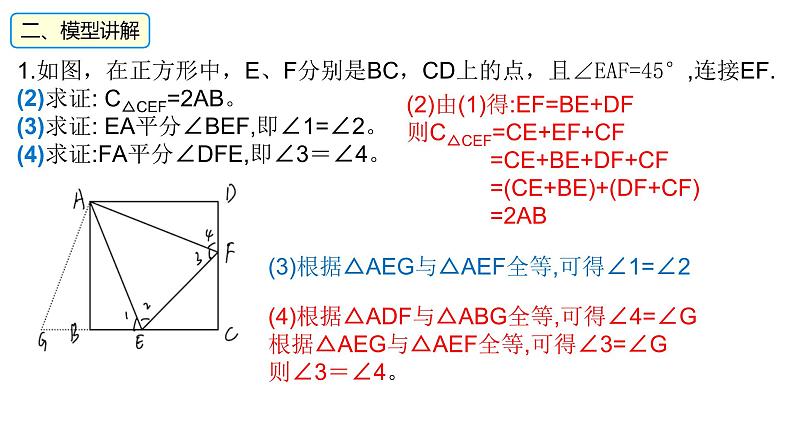
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(2)求证: C△CEF=2AB。(3)求证: EA平分∠BEF,即∠1=∠2。(4)求证:FA平分∠DFE,即∠3＝∠4。
(2)由(1)得:EF=BE+DF则C△CEF=CE+EF+CF =CE+BE+DF+CF =(CE+BE)+(DF+CF) =2AB
(3)根据△AEG与△AEF全等,可得∠1=∠2
(4)根据△ADF与△ABG全等,可得∠4=∠G根据△AEG与△AEF全等,可得∠3=∠G则∠3＝∠4。
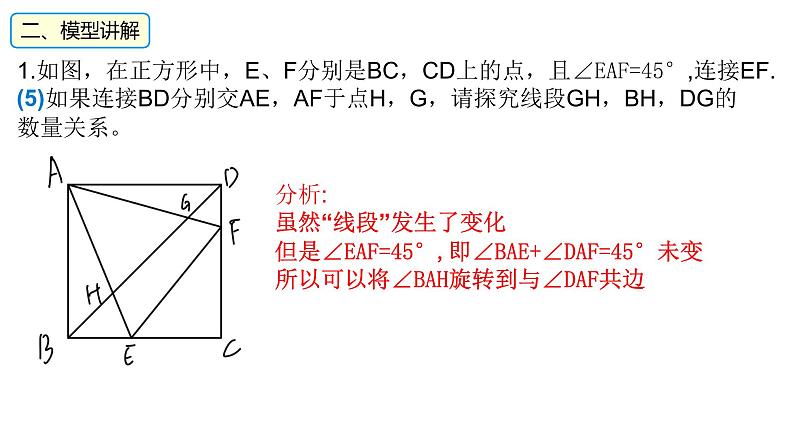
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(5)如果连接BD分别交AE，AF于点H，G，请探究线段GH，BH，DG的数量关系。
分析:虽然“线段”发生了变化但是∠EAF=45°,即∠BAE+∠DAF=45°未变所以可以将∠BAH旋转到与∠DAF共边
GH2=BH2+DG2理由如下:如图,△AHB与△AMD全等则BH=DM，∠1=∠2=45°。此时△AHG与△AMG全等,则MG=HG。又∠3=45°,所以∠MDG=90°。则MG2=MD2+DG2,所以GH2=BH2+DG2。
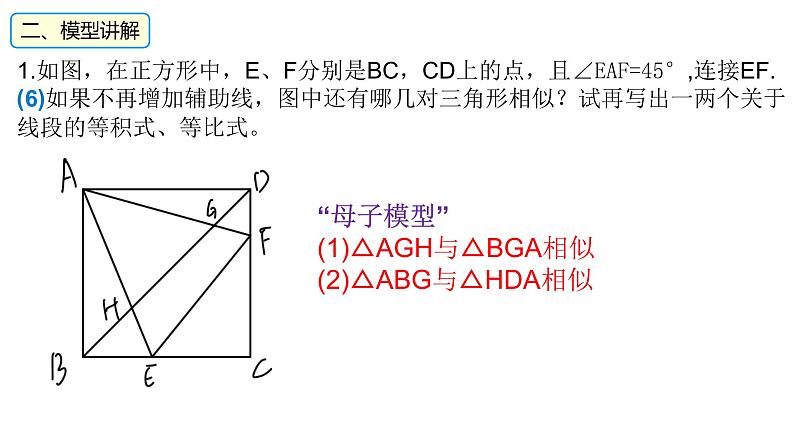
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(6)如果不再增加辅助线，图中还有哪几对三角形相似？试再写出一两个关于线段的等积式、等比式。
“母子模型”(1)△AGH与△BGA相似(2)△ABG与△HDA相似
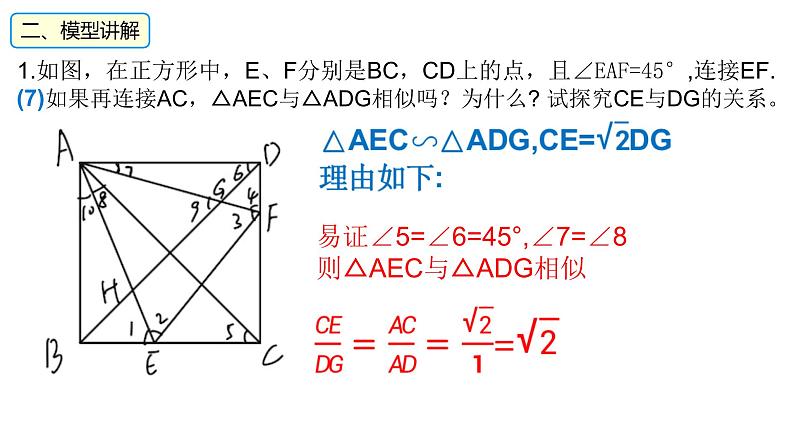
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(7)如果再连接AC，△AEC与△ADG相似吗？为什么? 试探究CE与DG的关系。
易证∠5=∠6=45°,∠7=∠8则△AEC与△ADG相似
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(8)追问1: 此时，△FCA与△HBA相似吗？为什么？试探究CF与BH的关系。
易证∠ABH=∠ACD=45°,∠10=∠FAC则△FCA与△HBA相似
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(9)追问2: 此时，△AEF与△AGH相似吗？为什么？试探究EF与GH的关系。
因为∠9=∠6+∠7=45°+∠7,∠7=∠8又因为∠8=45°-∠10所以∠9=45°+(45°-∠10)=90°-∠10因为∠2=∠1=90°-∠10所以∠2=∠9因为∠EAF=∠GAH(公共角)所以△AEF与△AGH相似
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(12)如果我们分别连接EG、FH，看看又可得到什么结论?
分析:因为点A、B、E、G四点共圆问题，可以根据圆中相交两弦的“形结构”来证明。由△AHG与△BHE相似,得AH：BH=HG：HE，即AH：HG=BH：HE.又∠AHB=∠GHE,所以△AHB与△GHE相似则∠HEG=∠HBA=45°。又∠EAF=45°,所以∠AGE=90°,即AG⊥EG。
同上点A、D、F、H四点共圆问题在证明∠AFH=45°
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(13)如果我们将CH连接起来，看看又可得到什么结论?
分析求tan∠HCF的值，有两个思考方向。(1)是将∠HCF放在直角三角形中，构造直角三角形，根据正切的定义求比值；(2)是找到一个与∠HCF相等的角, 用转化的思想来解决问题。
1.如图，在正方形中，E、F分别是BC，CD上的点，且∠EAF=45°,连接EF.(14)如果点E为BC边的中点，求tan∠HCF的值。
因为∠HCF=∠HAD=∠AEB,所以tan∠HCF=tan∠AEB=AB:BF=2