


所属成套资源:浙教版数学八年级上册全套同步教案
初中数学浙教版八年级上册1.3 证明精品第一课时教案
展开
这是一份初中数学浙教版八年级上册1.3 证明精品第一课时教案,共7页。教案主要包含了目测,列举,测量等内容,欢迎下载使用。
浙教版数学八年级上册 1.3证明(第一课时) 教案一、教材分析证明是初中几何教学中最主要的内容,它考验学生的逻辑推理能力,对于刚刚接触几何证明的初中生来说,如何有一直条件出发,根据已知的定义,公理,定理一步步推出结论成立,形成流畅的推理过程,并有条理的表达是很大的考验。 二、学情分析学生之前已经学习了三角形的基本知识,定义与命题,真假命题以及公理。定理等知识。也曾有过简单的说理,但规范的几何证明还没学习。本节课的学习是对他们之后进行有条理的进行证明的开始。学生的心理特征,八年级的学生好奇心重,求知欲强,教师通过合适的方法引入有助于他们更好理解掌握几何证明的相关内容。 三、教学目标知识与技能1.了解证明的含义。2、体验、理解证明的必要性和推理过程中要步步有据。3、了解证明的表达格式,会按规定格式证明简单命题。过程与方法:在学习的过程中发展初步的演绎推理能力情感态度与价值观:感受数学的严谨,初步养成言之有理、落笔有据的推理习惯,感受数学的魅力。四、教学重难点重点:证明的含义和表述格式难点:证明的基本步骤和书写格式,推理的合理性五、教学方法、手段教学方法:讲授法、比较法、推理法教学手段:板书与多媒体课件相结合 六.教学过程回顾旧知上节课我们学习了命题,回忆一下,要判定一个真命题,我们用了什么方法呢?(1)通过推理的方式,即根据已知的事实来推断未知事实;(2)人们经过长期实践后而公认为正确的.判定一个命题是假命题的方法: 举反例引入新课1.图中的四边形是正方形吗?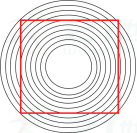 是正方形2.直观看到的有可能是假的。通过观察,先猜想结论,再动手验证: 如图,一组直线a,b,c,d是否都互相平行?
是正方形2.直观看到的有可能是假的。通过观察,先猜想结论,再动手验证: 如图,一组直线a,b,c,d是否都互相平行? 相互平行动手做一做命题“对于自然数n,代数式n2-3n+7的值都是质数”是真命题吗?A同学是这样解的:因为 当n=0时, n2-3n+7=7;当n=1时, n2-3n+7=5;当n=2时, n2-3n+7=5;当n=3时, n2-3n+7=7;当n=4时, n2-3n+7=11;……代数式 n2-3n+7 的值都是质数,所以命题是真的。你认为他解得对吗?不对 ,当n=6时, n2-3n+7=25
相互平行动手做一做命题“对于自然数n,代数式n2-3n+7的值都是质数”是真命题吗?A同学是这样解的:因为 当n=0时, n2-3n+7=7;当n=1时, n2-3n+7=5;当n=2时, n2-3n+7=5;当n=3时, n2-3n+7=7;当n=4时, n2-3n+7=11;……代数式 n2-3n+7 的值都是质数,所以命题是真的。你认为他解得对吗?不对 ,当n=6时, n2-3n+7=25![]() 枚举 举不胜举!4.图中线段AB与线段CD,哪条长?
枚举 举不胜举!4.图中线段AB与线段CD,哪条长?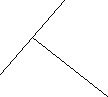 新课讲授 上面的例子说明了什么呢? 判断一个命题是真命题的方法有:一、目测(直观)二、列举三、测量可是这三种方法都存在一些误差,用目测的方法会产生错觉,列举会举不胜举,测量法会产生误差要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立,这样的推理过程叫做证明 。 例题精讲例1 已知:如图,DE∥BC,∠1=∠E,求证:BE平分∠ABC.
新课讲授 上面的例子说明了什么呢? 判断一个命题是真命题的方法有:一、目测(直观)二、列举三、测量可是这三种方法都存在一些误差,用目测的方法会产生错觉,列举会举不胜举,测量法会产生误差要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立,这样的推理过程叫做证明 。 例题精讲例1 已知:如图,DE∥BC,∠1=∠E,求证:BE平分∠ABC.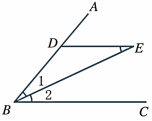 证明:∵ DE∥BC(已知),∴∠2=∠E(两直线平行,内错相等).∵∠1=∠E(已知),∴∠1=∠2,∴ BE平分∠ABC(角平分线的定义). 例2 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DEF.求证:∠PEF+∠PFE=90°
证明:∵ DE∥BC(已知),∴∠2=∠E(两直线平行,内错相等).∵∠1=∠E(已知),∴∠1=∠2,∴ BE平分∠ABC(角平分线的定义). 例2 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DEF.求证:∠PEF+∠PFE=90°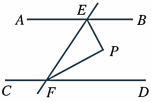 证明:∵ EP,FP分别平分∠BEF,∠DEF.∴ ∠PEF=
证明:∵ EP,FP分别平分∠BEF,∠DEF.∴ ∠PEF=![]() ∠BEF,∠PFE=
∠BEF,∠PFE=![]() ∠DFE.∵ AB∥CD,∴ ∠BEF+∠DEF=180°.∴ ∠PEF+∠PFE=
∠DFE.∵ AB∥CD,∴ ∠BEF+∠DEF=180°.∴ ∠PEF+∠PFE=![]() ∠BEF+
∠BEF+![]() ∠DFE =
∠DFE =![]() (∠BEF+∠DEF)=
(∠BEF+∠DEF)=![]() ×180°=90°. 小结:证明几何命题的基本思路:(1) 综合法:从已知出发,根据已知我们能得到什么?(2) 分析法:从求证出发,根据求证结论,我们需要什么?注意:(1)证明过程中的每一步推理都要有依据,依据作为推理的理由,可以写在每一步后的括号内.(2)证明角相等(或线段)相等的常用手段之一是找第三个角(或线段) 课堂检测:1.关于证明,下列说法不正确的是( )A.证明是说明命题是真命题的过程B.要判定一个命题是真命题常常通过推理的方式C.要说明一个命题是假命题常采用举反例的方式D.真命题与假命题都可以通过举反例来说明答案 D2.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )A.垂线段最短B.经过一点有无数条直线C.经过两点,有且仅有一条直线D.两点之间,线段最短答案D
×180°=90°. 小结:证明几何命题的基本思路:(1) 综合法:从已知出发,根据已知我们能得到什么?(2) 分析法:从求证出发,根据求证结论,我们需要什么?注意:(1)证明过程中的每一步推理都要有依据,依据作为推理的理由,可以写在每一步后的括号内.(2)证明角相等(或线段)相等的常用手段之一是找第三个角(或线段) 课堂检测:1.关于证明,下列说法不正确的是( )A.证明是说明命题是真命题的过程B.要判定一个命题是真命题常常通过推理的方式C.要说明一个命题是假命题常采用举反例的方式D.真命题与假命题都可以通过举反例来说明答案 D2.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )A.垂线段最短B.经过一点有无数条直线C.经过两点,有且仅有一条直线D.两点之间,线段最短答案D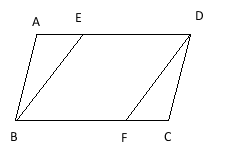 3.如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请补充完整证明过程,并在括号内填上相应依据:
3.如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请补充完整证明过程,并在括号内填上相应依据:
∵AD∥BC(已知),
∴∠1=∠3( 两直线平行,内错角相等 ),
∵∠1=∠2(已知),
∴∠2=∠3( 等量代换),
∴BE∥DF( 同位角相等,两直线平行 ),
∴∠3+∠4=180°( 两直线平行,同旁内角互补). 4.判断题(正确的画“√”,错误的画“×”)
(1)a、b、c是直线,且a∥b,b∥c,则a∥c.______
(2)a、b、c是直线,且a⊥b,b⊥c,则a⊥c.______.解:(1)∵如果两条直线都与第三条直线平行,那么这两条直线也互相平行,
∴a、b、c是直线,且a∥b,b∥c,则a∥c,故本小题正确;
(2)∵在同一平面内,垂直于同一条直线的两条直线互相平行,
∴a、b、c是直线,且a⊥b,b⊥c,则a∥c,故本小题错误. 5. 已知:如图1-12,DE∥BC,∠1=∠E.求证:BE平分∠ABC. 证明 ∵DE∥BC(已知),∴∠2=∠E(两直线平行,内错角相等). ∵∠1=∠E(已知),∴∠1=∠2,∴BE平分∠ABC(角平分线的定义). 6.已知:如图,直线
![]() 被直线
被直线![]() 所截,
所截,![]() 为垂足,
为垂足,![]() .
.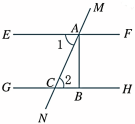 求证:
求证:![]() (填空).证明: ∵
(填空).证明: ∵ ![]() (已知),∴
(已知),∴ ![]() ∥
∥![]() (内错角相等,两直线平行),∴
(内错角相等,两直线平行),∴ ![]() (两直线平行,同旁内角互补).∵
(两直线平行,同旁内角互补).∵![]() (已知),∴
(已知),∴ ![]() (垂线的定义).∴
(垂线的定义).∴![]() ,∴
,∴![]() (垂线的定义) 7.已知:如图,
(垂线的定义) 7.已知:如图,![]() 于点
于点![]() 于点
于点![]() .求证:
.求证: ![]() ∥
∥![]()
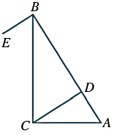 证明:∵
证明:∵![]() (已知),∴
(已知),∴![]() 90
90![]() (垂线的定义).∴
(垂线的定义).∴![]()
![]() (三角形三个内角的和等于
(三角形三个内角的和等于![]() ).∵
).∵![]() (已知),∴
(已知),∴![]() ∴
∴![]() ,∴
,∴![]() //
//![]() (同旁内角互补,两直线平行) 七.课堂小结,作业布置小结:1.证明的定义2.平行线相关的证明3.证明的基本步骤和格式作业:课本P18页第2、3、4 题 配套练习
(同旁内角互补,两直线平行) 七.课堂小结,作业布置小结:1.证明的定义2.平行线相关的证明3.证明的基本步骤和格式作业:课本P18页第2、3、4 题 配套练习
相关教案
这是一份初中数学浙教版八年级上册1.3 证明第二课时教案,共8页。教案主要包含了创设情景,引出课题等内容,欢迎下载使用。
这是一份沪科版八年级上册第13章 三角形中的边角关系、命题与证明13.2 命题与证明第一课时教案,共5页。教案主要包含了教材内容分析,学生学情分析,教学目标,教学重难点,教学过程设计,板书设计等内容,欢迎下载使用。
这是一份数学八年级上册1.3 证明教案设计,共2页。教案主要包含了画出命题的图形,结合图形写出已知等内容,欢迎下载使用。










