2020贵港中考数学

这是一份2020贵港中考数学，共14页。试卷主要包含了选择题每小题都给出标号为A，填空题，解答题等内容，欢迎下载使用。
2020年广西贵港市中考数学试卷
一、选择题（本大题共12小题，每小题3分，共36分）每小题都给出标号为A、B、C、D的四个选项，其中只有一个是正确的．请考生用2B铅笔在答题卡上将选定的答案标号涂黑．
1．（3分）﹣2的相反数是（　　）
A．﹣2 B．﹣ C．2 D．
2．（3分）若式子在实数范围内有意义，则实数x的取值范围是（　　）
A．x＜﹣1 B．x≥﹣1 C．x≥0 D．x≥1
3．（3分）目前世界上刻度最小的标尺是钻石标尺，它的最小刻度为0.2nm（其中1nm＝10﹣9m），用科学记数法表示这个最小刻度（单位：m），结果是（　　）
A．2×10﹣8m B．2×10﹣9m C．2×10﹣10m D．2×10﹣11m
4．（3分）数据2，6，5，0，1，6，8的中位数和众数分别是（　　）
A．0和6 B．0和8 C．5和8 D．5和6
5．（3分）下列运算正确的是（　　）
A．2a+3b＝5ab B．5a2﹣3a＝2a
C．（ab3）2＝a2b6 D．（a+2）2＝a2+4
6．（3分）一元二次方程x2﹣x﹣3＝0的根的情况为（　　）
A．有两个相等的实数根 B．有两个不相等的实数根
C．只有一个实数根 D．没有实数根
7．（3分）如果a＜b，c＜0，那么下列不等式中不成立的是（　　）
A．a+c＜b+c B．ac＞bc C．ac+1＞bc+1 D．ac2＞bc2
8．（3分）下列命题中真命题是（　　）
A．的算术平方根是2
B．数据2，0，3，2，3的方差是
C．正六边形的内角和为360°
D．对角线互相垂直的四边形是菱形
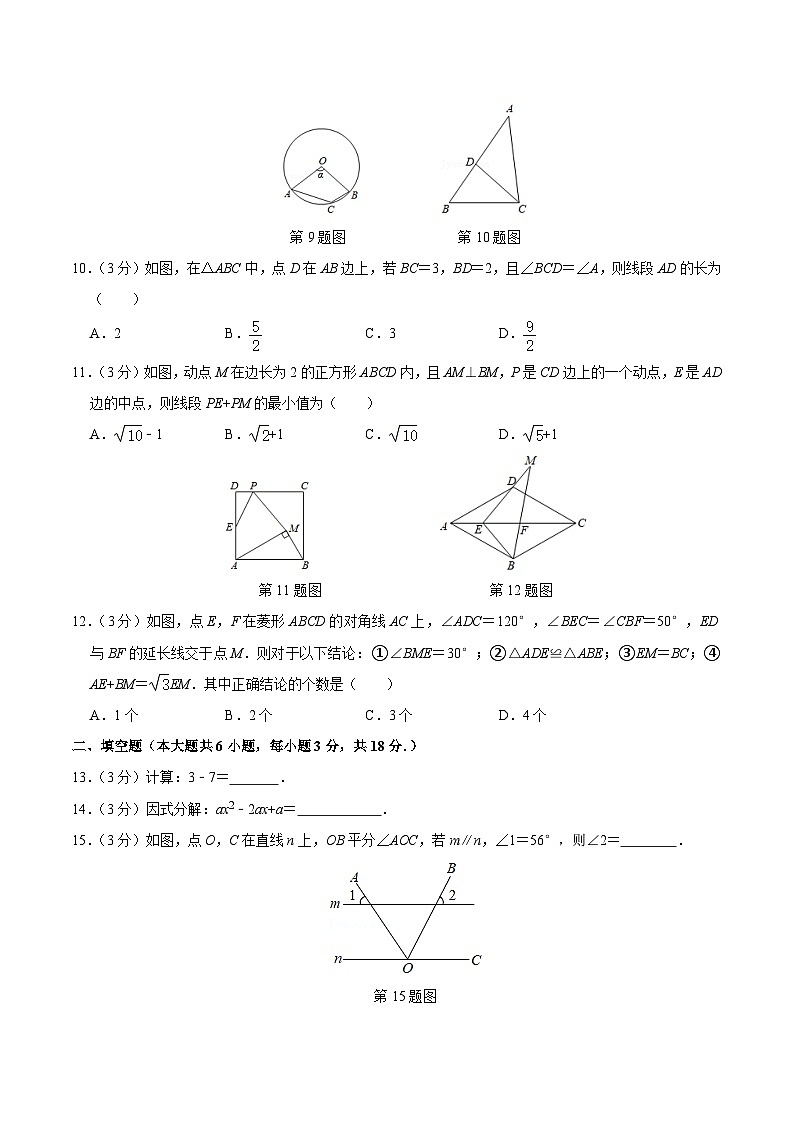
9．（3分）如图，点A，B，C均在⊙O上，若∠ACB＝130°，则∠α的度数为（　　）
A．100° B．110° C．120° D．130°

第9题图 第10题图
10．（3分）如图，在△ABC中，点D在AB边上，若BC＝3，BD＝2，且∠BCD＝∠A，则线段AD的长为（　　）
A．2 B． C．3 D．
11．（3分）如图，动点M在边长为2的正方形ABCD内，且AM⊥BM，P是CD边上的一个动点，E是AD边的中点，则线段PE+PM的最小值为（　　）
A．﹣1 B．+1 C． D．+1

第11题图 第12题图
12．（3分）如图，点E，F在菱形ABCD的对角线AC上，∠ADC＝120°，∠BEC＝∠CBF＝50°，ED与BF的延长线交于点M．则对于以下结论：①∠BME＝30°；②△ADE≌△ABE；③EM＝BC；④AE+BM＝EM．其中正确结论的个数是（　　）
A．1个 B．2个 C．3个 D．4个
二、填空题（本大题共6小题，每小题3分，共18分．）
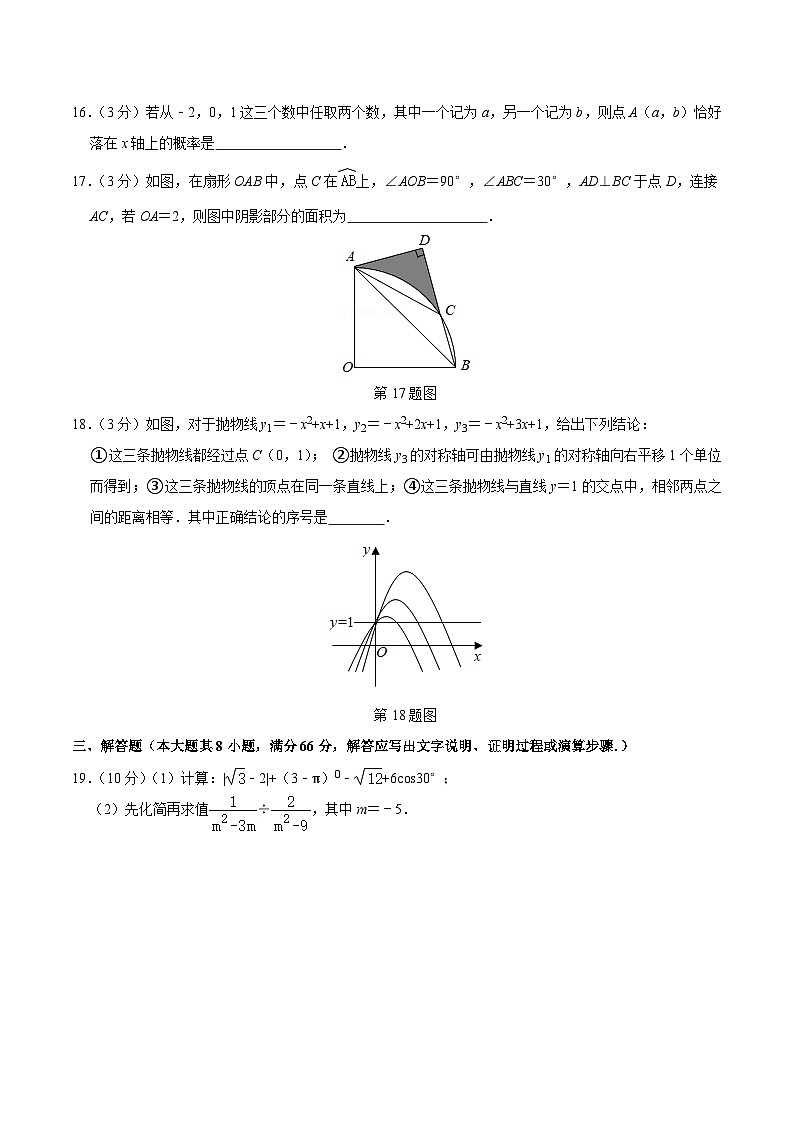
13．（3分）计算：3﹣7＝　 　．
14．（3分）因式分解：ax2﹣2ax+a＝　 　．
15．（3分）如图，点O，C在直线n上，OB平分∠AOC，若m∥n，∠1＝56°，则∠2＝　 　．

第15题图
16．（3分）若从﹣2，0，1这三个数中任取两个数，其中一个记为a，另一个记为b，则点A（a，b）恰好落在x轴上的概率是　 　．
17．（3分）如图，在扇形OAB中，点C在上，∠AOB＝90°，∠ABC＝30°，AD⊥BC于点D，连接AC，若OA＝2，则图中阴影部分的面积为　 　．

第17题图
18．（3分）如图，对于抛物线y1＝﹣x2+x+1，y2＝﹣x2+2x+1，y3＝﹣x2+3x+1，给出下列结论：
①这三条抛物线都经过点C（0，1）； ②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到；③这三条抛物线的顶点在同一条直线上；④这三条抛物线与直线y＝1的交点中，相邻两点之间的距离相等．其中正确结论的序号是　 　．

第18题图
三、解答题（本大题其8小题，满分66分，解答应写出文字说明、证明过程或演算步骤．）
19．（10分）（1）计算：|﹣2|+（3﹣π）0﹣+6cos30°；
（2）先化简再求值÷，其中m＝﹣5．






20．（5分）如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（1，4），B（4，1），C（4，3）．
（1）画出将△ABC向左平移5个单位得到的△A1B1C1；
（2）画出将△ABC绕原点O顺时针旋转90°得到的△A2B2C2．

第20题图




21．（6分）如图，双曲线y1＝（k为常数，且k≠0）与直线y2＝2x+b交于A（1，m）和B（n，n+2）两点．
（1）求k，m的值；
（2）当x＞0时，试比较函数值y1与y2的大小．

第21题图
22．（8分）某校对九年级学生进行“综合素质”评价，评价的结果分为A（优秀）、B（良好）、C（合格）、D（不合格）四个等级，现从中随机抽查了若干名学生的“综合素质”等级作为样本进行数据处理，并绘制以下两幅不完整的统计图．请根据统计图提供的信息，解答下列问题：
（1）B（良好）等级人数所占百分比是　 　；
（2）在扇形统计图中，C（合格）等级所在扇形的圆心角度数是　 　；
（3）请补充完整条形统计图；
（4）若该校九年级学生共1000名，请根据以上调查结果估算：评价结果为A（优秀）等级或B（良好）等级的学生共有多少名？

第22题图



23．（8分）在今年新冠肺炎防疫工作中，某公司购买了A、B两种不同型号的口罩，已知A型口罩的单价比B型口罩的单价多1.5元，且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同．
（1）A、B两种型号口罩的单价各是多少元？
（2）根据疫情发展情况，该公司还需要增加购买一些口罩，增加购买B型口罩数量是A型口罩数量的2倍，若总费用不超过3800元，则增加购买A型口罩的数量最多是多少个？





24．（8分）如图，在△ABC中，AB＝AC，点D在BC边上，且AD＝BD，⊙O是△ACD的外接圆，AE是⊙O的直径．
（1）求证：AB是⊙O的切线；
（2）若AB＝2，AD＝3，求直径AE的长．

第24题图




25．（11分）如图，已知抛物线y＝x2+bx+c与x轴相交于A（﹣6，0），B（1，0），与y轴相交于点C，直线l⊥AC，垂足为C．
（1）求该抛物线的表达式；
（2）若直线l与该抛物线的另一个交点为D，求点D的坐标；
（3）设动点P（m，n）在该抛物线上，当∠PAC＝45°时，求m的值．

第25题图
26．（10分）已知：在矩形ABCD中，AB＝6，AD＝2，P是BC边上的一个动点，将矩形ABCD折叠，使点A与点P重合，点D落在点G处，折痕为EF．
（1）如图1，当点P与点C重合时，则线段EB＝　 　，EF＝　 　；
（2）如图2，当点P与点B，C均不重合时，取EF的中点O，连接并延长PO与GF的延长线交于点M，连接PF，ME，MA．
①求证：四边形MEPF是平行四边形；
②当tan∠MAD＝时，求四边形MEPF的面积．

第26题图

　　2020年贵港市初中学业水平考试试卷

,快速对答案)

一、选择题(每小题3分)
1－5 CBCDC　6－10 BDBAB　11－12 AD
二、填空题(每小题3分)
13. －4　14. a(x－1)2　15. 62°　16.
17. 1＋－　18. ①②④
三、解答题标准答案及评分标准：
19－26题见PX
详解详析
1. C　2. B　3. C　4. D　5. C　6. B　7. D　
8. B　【解析】逐项分析如下：
选项
逐项分析
正误
A
等于2，∴2的算术平方根是

B
这组数据的平均数是＝2，∴s2＝[(2－2)2＋(0－2)2＋(3－2)2＋(2－2)2＋(3－2)2]÷5＝
√
C
正六边形的内角和为(6－2)×180°＝720°≠360°

D
对角线互相垂直的四边形可能是菱形或正方形或不规则图形

9. A　10. B　
11. A　【解析】∵AM⊥BM，∴点M在正方形内以AB为直径的半圆上，如解图，作点E关于DC的对称点Q，取AB的中点O，连接OQ，交半圆于点M，交DC于点P，由于两点之间线段最短，∴此时PE＋PM＝PQ＋PM＝QM的值最小，∵AO＝AB＝1，AQ＝AD＋DQ＝AD＋AD＝3，∴OQ＝＝，∴PE＋PM＝MQ＝OQ－OM＝－1.

　 第11题解图
12. D　【解析】∵四边形ABCD是菱形，∠ADC＝120°，∴∠DAC＝∠BAC＝∠BCA＝∠ACD＝30°，∵AC是对角线，∴点D与点B关于AC成轴对称，则EC平分∠DEB，∠BEC＝∠CBF＝∠MEC＝50°，∴∠EFB＝80°，∴∠BME＝30°，①正确；由AD＝AB，AE＝AE，∠DAE＝∠BAE，易证△ADE≌△ABE，②正确；∵∠EBF＝∠FEB＝50°，∠M＝∠ECB＝30°，BE＝EB，∴△BEM≌△EBC，∴EM＝BC，③正确；∵△BEM≌△EBC，∴BM＝EC，EM＝BC，∴AE＋BM＝AE＋EC＝AC.如解图，过点B作BG⊥AC于点G，∴CG＝AC，∴在Rt△CBG中，cos30°＝＝，∴AC＝2BC·cos30°＝BC＝EM.∴AE＋BM＝EM，④正确；综上所述，正确的结论有4个，故选D.

第12题解图
13. －4　14. a(x－1)2　15. 62°
16. 　【解析】列表如下：
横坐标a纵坐标b
－2
0
1
－2
不在x轴上
不在x轴上
不在x轴上
0
在x轴上
在x轴上
在x轴上
1
不在x轴上
不在x轴上
不在x轴上
∴点A(a，b)恰好落在x轴上的概率是.
17. 1＋－　【解析】如解图，连接OC，∵∠AOB＝90°，∴△OAB是等腰直角三角形，∵OA＝2，∴AB＝2，∵∠ABC＝30°，AD⊥BC于点D，∴AD＝AB＝×2＝，BD＝AB＝，∴S△ABD＝××＝，S△AOB＝×2×2＝2，过点C作CE⊥OB于点E，∵∠ABC＝30°，∴∠AOC＝60°，∴∠COB＝30°，∴CE＝OC＝1，∴S△OBC＝×2×1＝1，∴S阴影＝S△AOB＋S△ABD－S△OBC－S扇形AOC＝2＋－1－＝1＋－.

第17题解图
18. ①②④　【解析】①三条抛物线经过定点(0，1)正确(代入检验直接得出)；②抛物线y1的对称轴是直线x＝，抛物线y3的对称轴是直线x＝，因此②正确；③三条抛物线的顶点分别是(，)、(1，2)，(，)，自变量的值增加，函数值增加y2－y1＝2－＝；y3－y2＝－2＝，因此三个顶点不在同一条直线上，③错误；④当－x2＋x＋1＝1时，交点之间的距离是1，－x2＋2x＋1＝1时，交点之间的距离是2，2－1＝1，－x2＋3x＋1＝1时，交点之间的距离是3，3－2＝1，因此三条抛物线与y＝1交点中，相邻的两个交点之间的距离是1，都相等，因此④正确，∴结论正确的序号是①②④.
19. 解：(1)原式＝2－＋1－2＋6×(4分)
＝3－3＋3
＝3；(5分)
(2)原式＝·，(8分)
＝，(9分)
当m＝－5时，原式＝＝.(10分)
20. 解：(1)如解图，△A1B1C1即为所求；(2分)
(2)如解图，△A2B2C2即为所求．(5分)

第20题解图
21. 解：(1)将点B(n，n＋2)代入y2＝2x＋b中，得
n＋2＝2×n＋b，解得b＝2.
∴y2＝2x＋2，
把点A(1，m)代入y2＝2x＋2，得m＝2＋2＝4，
把点A(1，4)代入y1＝中，得k＝4；(3分)
(2)由(1)可知A(1，4)，
∴由题图可知，当0＜x＜1时，y1＞y2，(4分)
当x＝1时，y1＝y2，(5分)
当x＞1时，y1＜y2.(6分)
22. 解：(1)25%；(2分)
(2)72°；(4分)
(3)补充条形统计图如解图；

第22题解图


(4)1000×＝700(名)，
答：估计评价结果为A等级或B等级的学生共有700名．(8分)
23. 解：(1)设B型号口罩的单价是x元，则A型号口罩的单价是(x＋1.5)元，
结合题意列方程为：＝，
解得x＝2.5，
经检验，x＝2.5是原分式方程的根，且符合题意．
∴x＋1.5＝4，
答：A型号口罩的单价是4元，B型号口罩的单价是2.5元；(4分)
(2)设增加购买A型口罩m只，那么增加购买B型口罩2m只，
∴4m＋2.5×2m≤3800，解得m≤422，由于m是正整数，因此m的最大值是422，
答：增加购买A型口罩的数量最多是422只．(8分)
24. (1)证明：如解图，连接DE，则∠E＝∠C，

第24题解图
∵AE是⊙O的直径，
∴∠ADE＝90°，即∠DAE＋∠E＝90°.
在△ABC中，AB＝AC，
∴∠B＝∠C.
∵点D在BC上，且AD＝BD，
∴∠B＝∠BAD.
∴∠E＝∠BAD.
∴∠BAD＋∠DAE＝90°，即∠BAE＝90°.
∵OA是⊙O的半径，
∴AB是⊙O的切线；(4分)
(2)解：由(1)可知∠C＝∠BAD，
又∵∠B＝∠B，
∴△ABC∽△DBA，
∴＝，即＝，解得BC＝8.
∴DC＝BC－BD＝5，
∴cosC＝＝＝，
∵∠E＝∠C，∴cosE＝＝，设AE＝3x，则DE＝x，
∴AD＝＝x，
∵AD＝3，∴x＝3，∴x＝，
∴AE＝3.(8分)
25. 解：(1)由题可得抛物线的表达式是y＝(x＋6)(x－1)＝x2＋x－3；(3分)

第25题解图①
(2)由(1)可得C(0，－3)，∵A(－6，0)，设直线AC的解析式为y＝kx＋n，
则，解得，
∴直线AC的解析式是y＝－x－3，
如解图①，设直线l与x轴的交点为K，
∵直线l⊥AC，∴易得△OCK∽△OAC，
∴＝，即＝，解得OK＝，∴K(，0)，
∴直线l的解析式是y＝2x－3，
联立，
得x2＋x＝0，解得x1＝0，x2＝－1，
∴D(－1，－5)；(7分)
(3)①当点P在直线AC上方的抛物线上时，如解图②，延长AP交直线l于点M，作MN⊥y轴于点N，
∵l⊥AC，∠PAC＝45°，
∴△MAC是等腰直角三角形，∴AC＝CM，
∵∠AOC＝∠CNM＝∠ACM＝90°，
∴∠ACO＝∠CMN，∴△ACO≌△CMN，
∴MN＝OC＝3，CN＝AO＝6，∴ON＝3，
∴点M坐标为(3，3)，
∴直线AM的解析式是y＝x＋2，
联立，
得3x2＋13x－30＝0，解得x1＝－6(舍去)，x2＝，
当x时，y＝x＋2＝，
∴点P的坐标是(，)；(9分)

图② 图③
第25题解图
②当点P位于直线AC下方的抛物线上时，如解图③，作点M关于点C的对称点F，
根据点的平移可得出点F坐标是(－3，－3－6)，即(－3，－9)．
易得经过点A与点F的直线的解析式是y＝－3x－18，
联立，
解得x3＝－6(舍去)，x4＝－5，
当x＝－5时，y＝－3×(－5)－18＝－3，
∴点P的坐标是(－5，－3)，
综上所述，m的值为或－5.(11分)
,　难点突破) 第(2)问难点在于利用相似求出直线l的解析式，然后联立方程组求交点的横坐标；第(3)问的难点是分情况讨论点P的位置，通过求得AP延长线与l的交点坐标，进而得到AP所在直线的解析式为解题突破口．
26. (1)解：2，4；(2分)
,　解法提示) 设EB＝x，∴CE＝AE＝6－x，
在Rt△BCE中，CE2＝BE2＋BC2，即(6－x)2＝x2＋(2)2，解得x＝2，∴EB＝2，
∵∠FCG＋∠FCE＝90°，∠FCE＋∠BCE＝90°，
∴∠FCG＝∠BCE，
∵CG＝AD＝CB，∠G＝∠B＝90°，

第26题解图①
∴△CFG≌△CEB，∴DF＝GF＝EB＝2，
如解图①，过点F作FM⊥AB于点M，∴AM＝DF＝2，则ME＝AB－AM－BE＝6－2－2＝2，
∴EF＝＝＝4；

(2)①证明：∵DC∥AB，
∴FG∥EP，即MF∥PE.
∴∠MFO＝∠PEO.
∵点O是EF的中点，
∴OE＝OF，
又∵∠FOM＝∠EOP，∴△FOM≌△EOP，∴FM＝EP，
∴四边形MEPF是平行四边形；(6分)
②解：如解图②，连接AO，AP.

第26题解图②
由折叠性质可得AO＝PO，
由①得四边形MEPF是平行四边形，
∴MO＝PO，
∴AO＝PO＝MO＝MP，
∴△PAM是直角三角形，
∴∠MAP＝90°.
∵∠DAB＝90°，∴∠MAD＋∠DAP＝∠DAP＋∠PAB，
即∠MAD＝∠PAB.(8分)
∵tan∠MAD＝，
∴在Rt△ABP中，tan∠PAB＝＝，
∴BP＝AB·tan∠PAB＝6×＝2.
设PE的长为x，则BE＝6－x，
在Rt△PBE中，BE2＋BP2＝PE2，
即(6－x)2＋4＝x2，解得x＝，
∵PG⊥MG，
∴S四边形MEPF＝PE·PG＝×2＝.(10分)
,　难点突破)本题的难点在于第(2)②问，结合折叠的性质求得∠MAD＝∠PAB是解题的关键，再利用勾股定理求得PE的长即可．