第6章实数同步练习题（沪科版七下）

这是一份第6章实数同步练习题（沪科版七下），共7页。
6.2　实数同步练习题第1课时　实数的概念及分类基础题知识点1　无理数1．以下说法正确的是(B)A．无限小数都是无理数B．无限不循环小数是无理数C．无理数是带根号的数D．分数是无理数2．(2019·池州期末)下列各数：－2，0，，0.020020002…，π，，其中无理数的个数是(C)A．4       B．3       C．2       D．1知识点2　实数的概念及分类3．下列说法正确的是(D)A．实数包括有理数、无理数和零B．有理数包括正有理数和负有理数C．无限不循环小数和无限循环小数都是无理数D．无论是有理数还是无理数都是实数4．在①3.1414；②；③－；④；⑤2.；⑥－π中，属于有理数的有①③④⑤，属于正无理数的有②，属于负无理数的有⑥．(填序号)知识点3　循环小数与分数互化5．0.化成分数为(A)A.        B.        C.        D.6.化成小数为0.14__28__．易错点　对无理数的判断有误7．下列说法正确的是(D)A.是分数              B.是无理数C.π－3.14是有理数       D.是有理数中档题8．(2019·马鞍山期末)下列结论正确的是(D)A．带根号的数都是无理数B．立方根等于本身的数是0C．－没有立方根D．无理数是无限不循环小数9．(2018·滁州月考)有一个数值转换器，原理如下，当输入的x为64时，输出的y是(B)A．8       B.        C.        D.10．把下列各数分别填在相应的横线上．，－3，0，，0.3，，－1.732，，，，－，－，3＋，0.1010010001…(两个1之间依次增加一个0)．(1)整数：－3，0，，；(2)分数：0.3，，－1.732；(3)正数：，，0.3，，，3＋，0.101__001__000__1…(两个1之间依次增加一个0)；(4)负数：－3，－1.732，，，－， －；(5)有理数：-3，0,0.3 ，，-1.732，  ；(6)无理数：，，，－，－，3＋，0.101__001__000__1…(两个1之间依次增加一个0)．
第2课时　实数的运算与大小比较基础题知识点1　相反数、倒数、绝对值1．(2019·淮南期中)－的相反数是(C)A.        B．－       C.        D．－2.的倒数是(A)A.        B．－       C.        D．－3．－是的(A)A．相反数       B．倒数       C．绝对值       D．算术平方根4．(2019·遂宁)－|－|的值为(B)A.        B．－        C．±        D．25.－的相反数是－．知识点2　实数与数轴6．(2019·合肥期末)将四个数－，，，表示在数轴上，被如图所示的墨迹覆盖的数是(D)A．－       B.        C.        D.7．实数a，b在数轴上对应的点的位置如图所示，计算|a－b|的结果为(C)A．a＋b       B．a－b       C．b－a       D．－a－b8．(教材P20复习题B组T5变式)如图，圆的直径为1个单位长度，该圆上的点A与数轴上表示－1的点重合，将该圆沿数轴滚动1周，点A到达点B的位置，则点B表示的数是(D)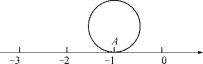A．π－1              B．－π－1C．－π＋1              D．π－1或－π－19．(2018·安徽月考)如图，在数轴上点A和点B表示的数之间的整数是2．知识点3　实数的近似计算10．(教材P15练习T4变式)(2019·马鞍山期末)无理数＋1在两个整数之间，下列结论正确的是(B)A．在2～3之间              B．在3～4之间
C．在4～5之间              D．在5～6之间11．近似计算(精确到0.1)：(1)＋；解：原式≈1.41＋1.73＝3.14≈3.1. (2)×.解：原式≈1.91×2.24＝4.2784≈4.3. 知识点4　实数的大小比较12．(2019·荆州)下列实数中最大的是(D)A.        B．π        C.        D．|－4|13．如图，数轴上A，B两点分别对应实数a，b，则下列结论正确的是(C)A．a<b       B．a＝b       C．a>b       D．ab>014．(教材P16习题T4(4)变式)(2018·合肥四十五中期中)比较大小：－>－5.4.(填“＞”“＜”或“＝”)15．(2019·淮南期中)写出一个比－π大的负无理数：答案不唯一，如：－．16．在数轴上作出表示下列各数的点，比较它们的大小，并用“＜”连接它们．，－1.5，，π，3，|－2|.解：数轴略．－1.5＜＜＜3＜π＜|－2|. 中档题17．下列各组数中互为相反数的一组是(C)A．－|－2|与B．－4与－C．－与||D．－与18．(2019·蚌埠期末)若整数n满足n＜2＜n＋1，则n的值为(A)A．4       B．5       C．6       D．719．若a，b均为正整数，且a>，b<，则a＋b的最小值是(B)A．3       B．4       C．5       D．620．【数形结合思想】(2018·安徽月考)如图，数轴上表示2，的对应点分别为C，B，点C是AB的中点，则点A表示的数是(C)A．－       B．2－       C．4－       D.－221．请写出两个你熟悉的大于2且小于3的无理数：答案不唯一，如：，．22．对于任意两个不相等的实数a，b，定义一种运算如下：ab＝，如32＝＝，那么8 5＝．23．比较下列各组两个数的大小：(1)－和－3；解：－＞－3.(2)6和；解：6＞. (3)2和.解：2＜. 24．近似计算(精确到0.01)：(1)2－3＋π；解：原式≈－1.33. (2)－10.解：原式≈－22.22. 综合题25．(1)比较下列各算式的大小：42＋32>2×4×3；(－2)2＋12>2×(－2)×1；()2＋()2>2××；()2＋()2＝2××；…(2)通过观察归纳，用字母表示你发现的规律：a2＋b2≥2ab．小专题(一)　实数大小比较的几种常用方法 方法1　利用数轴比较实数大小【例1】　在数轴上作出表示下列各数的点，比较它们的大小，并用“＜”连接它们．0，π，－，，|－1|，，.【解答】　在数轴上表示各数略．－＜0＜＜|－1|＜＜π＜.　利用数轴比较实数大小时，首先应找到实数在数轴上对应的位置，再根据“数轴上右边的点所表示的数总是大于左边的点所表示的数”比较大小即可．1．在数轴上表示下列各数，再用“＞”把它们连接起来．－3，，－，|－4|，，.解：在数轴上表示各数略．|－4|＞＞＞－＞－3＞. 方法2　利用平方法比较实数大小【例2】　比较3和的大小．【解答】　因为32＝9，()2＝10，9＜10，所以3＜.　比较含有无理数的式子的大小时，先将要比较的两个数分别平方，再根据“在a＞0，b＞0时，可由a2＞b2得到a＞b”比较大小．也就是说，两个正数比较大小时，如果一个数的平方比另一个数的平方大，则这个数大于另一个数．2．比较－和－3的大小．解：因为()3＝26，33＝27，26＜27，所以＜3.所以－＞－3. 方法3　利用作差法比较实数大小【例3】　比较和的大小．【解答】　因为－＝，<3，所以<0.所以<.　对于含有无理数的分数或小数比较大小时，通常用作差法．设a，b为任意两个实数，先求出a与b的差，再根据“当a－b＜0时，a＜b；当a－b＝0时，a＝b；当a－b＞0时，a＞b”来比较a与b的大小．3．比较1－和1－的大小．解：因为1－－(1－)＝－＞0，所以1－＞1－. 方法4　利用近似值法比较实数大小【例4】　比较－和－的大小．【解答】　因为－≈－0.67，－≈－≈－0.61，－0.67＜－0.61，所以－＜－.　在比较两个实数的大小时，如果有计算器，可以先用计算器求出它们的近似值，不过取近似值时，要使它们的精确度相同，再通过比较它们的近似值的大小，从而确定它们的大小．4．比较π和的大小．解：因为π≈3.14，≈＝3.12，3.14＞3.12，所以π＞.