七年级下册8.1 幂的运算获奖第2课时教学设计

第2课时 负整数次幂及其应用

【知识与技能】

1.了解零指数幂和负整数指数幂的意义.会进行化简或计算.

2.会用科学记数法表示绝对值小于1的数.

【过程与方法】

经历探索零指数幂和负整数指数幂的运算性质的过程，体会由特殊到一般、类比等数学思想方法，提高观察、分析和归纳的能力.

【情感态度】

通过参与数学学习活动，让学生在独立思考的基础上，积极参与数学问题的讨论，增强合作交流意识，积累解决问题的经验.

【教学重点】

零指数幂和负整数指数幂的运算顺序及科学记数法.

【教学难点】

零指数幂和负整数指数幂的运算性质的探究过程.

一、情境导入，初步认识

问题正方体甲的体积为103cm3，正方体乙的体积为105cm3，正方体甲的体积是正方体乙体积的几分之几？

【教学说明】

教师提出问题，学生很容易列出算式，初步感受被除式的指数小于或等于除式的指数这种情形的存在，激发学生探求新知识的欲望.

二、思考探究，获取新知

1.零指数幂和负整数指数幂.

探究：我们已经得到了当m>n时，am÷an(a≠0)的运算法则，那么当m≤n(m,n都是正整数）时，am÷an(a≠0)又如何计算呢？

（1）当被除式的指数等于除式的指数（即m=n）时，例如，

33÷33,108÷108,an÷an.

容易看出所得的商都是1，另一方面，仿照同底数幂的除法性质进行计算，得

（2）当被除式的指数小于除式的指数（即m<n)时，例如:32÷35,104÷108,am÷an.

那么可以通过分数约分，得

另一方面，仿照同底数幂的除法性质进行计算，得

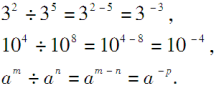
（3）观察上面的式子，你有什么发现呢？

【教学说明】

教师提出问题，学生思考分析、相互交流，通过观察两种计算方法，归纳零指数幂和负整数指数幂的运算性质.

【归纳结论】

任何一个不等于零的数的零次幂都等于1，即a0=1(a≠0);任何一个不等于零的数的-p(p是正整数）次幂，等于这个数的p次幂的倒数，即a-p=1/ap(a≠0，p是正整数）.

注意：再遇到计算am÷an时，就不必限制m>n，且正整数次幂的运算性质同样适合于零次幂和负整数次幂.

2.用科学记数法表示较小的数.问题：前面我们学过用科学记数法表示一些绝对值大于10的数，例如228000可记作

2.28×106.那么，绝对值小于1的数如何表示呢？

观察：

【教学说明】

教师提出问题，学生思考分析、相互交流，归纳用科学记数法表示较小数的方法.

【归纳结论】

绝对值小于1的数可记作a×10-n的表达式，其中1≤a<10,n是正整数，n等于原数中第一个不等于零的数字前面的零的个数（包括小数点前面的一个零），这种记数方法叫作科学记数法.

三、典例精析，掌握新知

例1计算：

例2用科学记数法表示下列各数：

(1)0.00076;

(2)-0.000001.59.

【解】

（1）0.00076=7.6×0.0001=7.6×10-4.

(2)-0.00000159=-1.59×0.000001=-1.59×10-6.

【教学说明】学生独立自主完成，教师选取部分学生上台展示自己的答案，加深对新学知识的理解和运用.

四、运用新知，深化理解

1.计算：

2.计算:

(1)(-x)10÷(-x)7;

(2)(-m)5÷(-m)9;

(3)4m+2÷4m-2;(4)(xy)5÷(-xy)2;

(5)(-2xy)5÷(-2xy)5.

3.用分数或小数表示下列各数:

4.用科学记数法表示下列各数：

0.0602,-0.00602,0.0000602,53.8,-34000

5.水是由氢、氧两种元素组成的，1个氢原子的质量为1.674×10-27kg，1个氧原子的质量为2.657×10-26kg，1个氢原子与1个氧原子的质量哪个大？

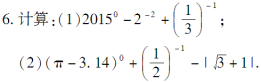
【教学说明】教师给出习题，学生独立自主完成，教师巡视，对有问题的学生及时予以指正.教师也可选取几个学生上台在黑板上演算,然后给予点评.

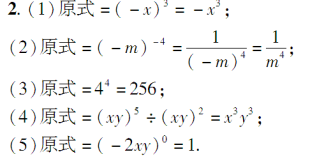
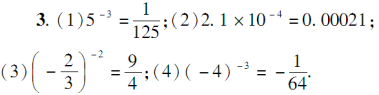
五、师生互动，课堂小结

通过这节课的学习，你掌握了哪些新知识？还有哪些疑问？请与同伴交流.

【教学说明】

学生相互交流，回顾零指数幂和负整数指数幂的运算性质，以及用科学记数法表示较小数的方法，进行知识的提炼和归纳.

完成练习册中本课时练习.

从实际问题引出零次幂和负整数次幂，再探究它们的运算性质，学生积极主动，体验应用知识的成就感，增强学好数学的信心.