第10章相交线平行线与平移知识点精讲(沪科版七下)
展开
这是一份第10章相交线平行线与平移知识点精讲(沪科版七下),共7页。
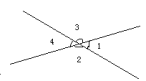
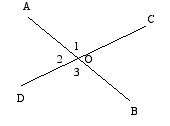
相交线与平行线知识点精讲相交线同一平面中,两条直线的位置有两种情况:相交:如图所示,直线AB与直线CD相交于点O,其中以O为顶点共有4个角: ![]() 1,
1,![]() 2,
2,![]() 3,
3,![]() 4;邻补角:其中
4;邻补角:其中![]() 1和
1和![]() 2有一条公共边,且他们的另一边互为反向延长线。像
2有一条公共边,且他们的另一边互为反向延长线。像![]() 1和
1和![]() 2这样的角我们称他们互为邻补角;对顶角:
2这样的角我们称他们互为邻补角;对顶角:![]() 1和
1和![]() 3有一个公共的顶点O,并且
3有一个公共的顶点O,并且![]() 1的两边分别是
1的两边分别是![]() 3两边的反向延长线,具有这种位置关系的两个角,互为对顶角;
3两边的反向延长线,具有这种位置关系的两个角,互为对顶角;![]() 1和
1和![]() 2互补,
2互补,![]() 2和
2和![]() 3互补,因为同角的补角相等,所以
3互补,因为同角的补角相等,所以![]() 1=
1=![]() 3。所以,对顶角相等例题:1.如图,3
3。所以,对顶角相等例题:1.如图,3![]() 1=2
1=2![]() 3,求
3,求![]() 1,
1,![]() 2,
2,![]() 3,
3,![]() 4的度数。
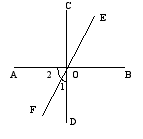
4的度数。 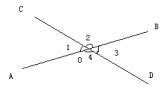 2.如图,直线AB、CD、EF相交于O,且
2.如图,直线AB、CD、EF相交于O,且![]() ,
,![]() ,则
,则![]() _______,
_______,![]() __________。
__________。
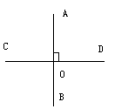
 垂直:垂直是相交的一种特殊情况两条直线相互垂直,其中一条叫做另一条的垂线,它们的交点叫做垂足。如图所示,图中AB
垂直:垂直是相交的一种特殊情况两条直线相互垂直,其中一条叫做另一条的垂线,它们的交点叫做垂足。如图所示,图中AB![]() CD,垂足为O。垂直的两条直线共形成四个直角,每个直角都是90
CD,垂足为O。垂直的两条直线共形成四个直角,每个直角都是90![]() 。 例题:如图,AB
。 例题:如图,AB![]() CD,垂足为O,EF经过点O,
CD,垂足为O,EF经过点O,![]() 1=26
1=26![]() ,求
,求![]() EOD,
EOD,![]() 2,
2,![]() 3的度数。
3的度数。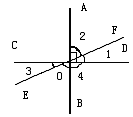 垂线相关的基本性质:(1) 经过一点有且只有一条直线垂直于已知直线;(2) 连接直线外一点与直线上各点的所有线段中,垂线段最短;(3) 从直线外一点到直线的垂线段的长度,叫做点到直线的距离。例题:假设你在游泳池中的P点游泳,AC是泳池的岸,如果此时你的腿抽筋了,你会选择那条路线游向岸边?为什么?
垂线相关的基本性质:(1) 经过一点有且只有一条直线垂直于已知直线;(2) 连接直线外一点与直线上各点的所有线段中,垂线段最短;(3) 从直线外一点到直线的垂线段的长度,叫做点到直线的距离。例题:假设你在游泳池中的P点游泳,AC是泳池的岸,如果此时你的腿抽筋了,你会选择那条路线游向岸边?为什么?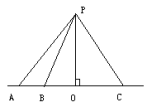 2.平行线:在同一个平面内永不相交的两条直线叫做平行线。平行线公理:经过直线外一点,有且只有一条直线和已知直线平行。
2.平行线:在同一个平面内永不相交的两条直线叫做平行线。平行线公理:经过直线外一点,有且只有一条直线和已知直线平行。![]() 如上图,直线a与直线b平行,记作a//b3.同一个平面中的三条直线关系:三条直线在一个平面中的位置关系有4中情况:有一个交点,有两个交点,有三个交点,没有交点。(1)有一个交点:三条直线相交于同一个点,如图所示,以交点为顶点形成各个角,可以用角的相关知识解决;
如上图,直线a与直线b平行,记作a//b3.同一个平面中的三条直线关系:三条直线在一个平面中的位置关系有4中情况:有一个交点,有两个交点,有三个交点,没有交点。(1)有一个交点:三条直线相交于同一个点,如图所示,以交点为顶点形成各个角,可以用角的相关知识解决;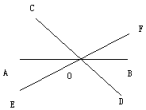 例题:如图,直线AB,CD,EF相交于O点,
例题:如图,直线AB,CD,EF相交于O点,![]() DOB是它的余角的两倍,
DOB是它的余角的两倍,![]() AOE=2
AOE=2![]() DOF,且有OG
DOF,且有OG![]() OA,求
OA,求![]() EOG的度数。
EOG的度数。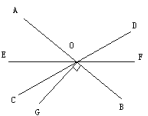 (2)有两个交点:(这种情况必然是两条直线平行,被第三条直线所截。)如图所示,直线AB,CD平行,被第三条直线EF所截。这三条直线形成了两个顶点,围绕两个顶点的8个角之间有三种特殊关系:*同位角:没有公共顶点的两个角,它们在直线AB,CD的同侧,在第三条直线EF的同旁(即位置相同),这样的一对角叫做同位角;*内错角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的两旁(即位置交错),这样的一对角叫做内错角;*同旁内角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的同旁,这样的一对角叫做同旁内角;
(2)有两个交点:(这种情况必然是两条直线平行,被第三条直线所截。)如图所示,直线AB,CD平行,被第三条直线EF所截。这三条直线形成了两个顶点,围绕两个顶点的8个角之间有三种特殊关系:*同位角:没有公共顶点的两个角,它们在直线AB,CD的同侧,在第三条直线EF的同旁(即位置相同),这样的一对角叫做同位角;*内错角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的两旁(即位置交错),这样的一对角叫做内错角;*同旁内角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的同旁,这样的一对角叫做同旁内角;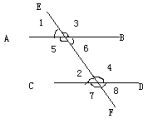 指出上图中的同位角,内错角,同旁内角。两条直线平行,被第三条直线所截,其同位角,内错角,同旁内角有如下关系:两直线平行,被第三条直线所截,同位角相等; 两直线平行,被第三条直线所截,内错角相等两直线平行,被第三条直线所截,同旁内角互补。如上图,指出相等的各角和互补的角。例题:1.如图,已知
指出上图中的同位角,内错角,同旁内角。两条直线平行,被第三条直线所截,其同位角,内错角,同旁内角有如下关系:两直线平行,被第三条直线所截,同位角相等; 两直线平行,被第三条直线所截,内错角相等两直线平行,被第三条直线所截,同旁内角互补。如上图,指出相等的各角和互补的角。例题:1.如图,已知![]() 1+
1+![]() 2=180
2=180![]() ,
,![]() 3=180
3=180![]() ,求
,求![]() 4的度数。 2.如图所示,AB//CD,
4的度数。 2.如图所示,AB//CD,![]() A=135
A=135![]() ,
,![]() E=80
E=80![]() 。求
。求![]() CDE的度数。
CDE的度数。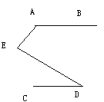 平行线判定定理:两条直线平行,被第三条直线所截,形成的角有如上所说的性质;那么反过来,如果两条直线被第三条直线所截,形成的同位角相等,内错角相等,同旁内角互补,是否能证明这两条直线平行呢?答案是可以的。两条直线被第三条直线所截,以下几种情况可以判定这两条直线平行:平行线判定定理1:同位角相等,两直线平行如图所示,只要满足
平行线判定定理:两条直线平行,被第三条直线所截,形成的角有如上所说的性质;那么反过来,如果两条直线被第三条直线所截,形成的同位角相等,内错角相等,同旁内角互补,是否能证明这两条直线平行呢?答案是可以的。两条直线被第三条直线所截,以下几种情况可以判定这两条直线平行:平行线判定定理1:同位角相等,两直线平行如图所示,只要满足![]() 1=
1=![]() 2(或者
2(或者![]() 3=
3=![]() 4;
4;![]() 5=
5=![]() 7;
7;![]() 6=
6=![]() 8),就可以说AB//CD平行线判定定理2:内错角相等,两直线平行如图所示,只要满足
8),就可以说AB//CD平行线判定定理2:内错角相等,两直线平行如图所示,只要满足![]() 6=
6=![]() 2(或者
2(或者![]() 5=
5=![]() 4),就可以说AB//CD平行线判定定理3:同旁内角互补,两直线平行
4),就可以说AB//CD平行线判定定理3:同旁内角互补,两直线平行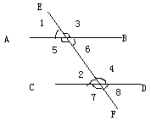
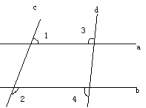 如图所示,只要满足
如图所示,只要满足![]() 5+
5+![]() 2=180
2=180![]() (或者
(或者![]() 6+
6+![]() 4=180
4=180![]() ),就可以说AB//CD平行线判定定理4:两条直线同时垂直于第三条直线,两条直线平行这是两直线与第三条直线相交时的一种特殊情况,由上图中
),就可以说AB//CD平行线判定定理4:两条直线同时垂直于第三条直线,两条直线平行这是两直线与第三条直线相交时的一种特殊情况,由上图中![]() 1=
1=![]() 2=90
2=90![]() 就可以得到。平行线判定定理5:两条直线同时平行于第三条直线,两条直线平行 例题:1.已知:AB//CD,BD平分
就可以得到。平行线判定定理5:两条直线同时平行于第三条直线,两条直线平行 例题:1.已知:AB//CD,BD平分![]() ,DB平分
,DB平分![]() ,求证:DA//BC
,求证:DA//BC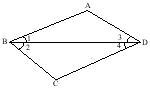 2.已知:AF、BD、CE都为直线,B在直线AC上,E在直线DF上,且
2.已知:AF、BD、CE都为直线,B在直线AC上,E在直线DF上,且![]() ,
,![]() ,求证:
,求证:![]() 。
。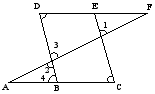 (3)有三个交点当三条直线两两相交时,共形成三个交点,12个角,这是三条直线相交的一般情况。如下图所示:
(3)有三个交点当三条直线两两相交时,共形成三个交点,12个角,这是三条直线相交的一般情况。如下图所示: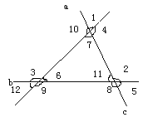 你能指出其中的同位角,内错角和同旁内角吗?三个交点可以看成一个三角形的三个顶点,三个交点直线的线段可以看成是三角形的三条边。(4)没有交点:这种情况下,三条直线都平行,如下图所示:
你能指出其中的同位角,内错角和同旁内角吗?三个交点可以看成一个三角形的三个顶点,三个交点直线的线段可以看成是三角形的三条边。(4)没有交点:这种情况下,三条直线都平行,如下图所示: 即a//b//c。这也是同一平面内三条直线位置关系的一种特殊情况。例题:如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与CD有怎样的位置关系,为什么?
即a//b//c。这也是同一平面内三条直线位置关系的一种特殊情况。例题:如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与CD有怎样的位置关系,为什么? 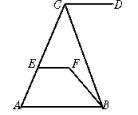
 一.选择题: 1. 如图,下面结论正确的是( ) A.
一.选择题: 1. 如图,下面结论正确的是( ) A. ![]() 是同位角 B.
是同位角 B. ![]() 是内错角 C.
是内错角 C. ![]() 是同旁内角 D.
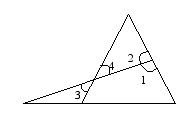
是同旁内角 D. ![]() 是内错角 2. 如图,图中同旁内角的对数是( ) A. 2对 B. 3对 C. 4对 D. 5对 3. 如图,能与
是内错角 2. 如图,图中同旁内角的对数是( ) A. 2对 B. 3对 C. 4对 D. 5对 3. 如图,能与![]() 构成同位角的有( ) A. 1个 B. 2个 C. 3个 D. 4个 4. 如图,图中的内错角的对数是( ) A. 2对 B. 3对 C. 4对 D. 5对
构成同位角的有( ) A. 1个 B. 2个 C. 3个 D. 4个 4. 如图,图中的内错角的对数是( ) A. 2对 B. 3对 C. 4对 D. 5对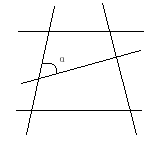
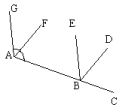 5.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少
5.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少![]() ,那么这两个角是( ) A.
,那么这两个角是( ) A. ![]() B. 都是
B. 都是![]()
 C.
C. ![]() 或
或![]() D. 以上都不对二.填空1. 已知:如图,
D. 以上都不对二.填空1. 已知:如图,![]() 。求证:
。求证:![]() 。证明:
。证明:![]() ( )
( )
![]() ( )
( ) ![]()
![]() ( )
( ) ![]()
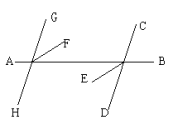
![]() ( )2. 已知:如图,COD是直线,
( )2. 已知:如图,COD是直线,![]() 。求证:A、O、B三点在同一条直线上。
。求证:A、O、B三点在同一条直线上。 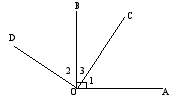 证明:
证明:![]() COD是一条直线( )
COD是一条直线( ) ![]() ___________( )
___________( ) ![]() ( )
( ) ![]() __________
__________![]() __________
__________ ![]() _______________( )三.解答题1.如图,已知:AB//CD,求证:
_______________( )三.解答题1.如图,已知:AB//CD,求证:![]() B+
B+![]() D+
D+![]() BED=
BED=![]() (至少用三种方法)
(至少用三种方法)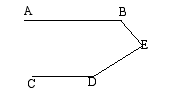 2.已知:如图,E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,
2.已知:如图,E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,![]() A=
A=![]() D,
D,![]() 1=
1=![]() 2,求证:
2,求证:![]() B=
B=![]() C。
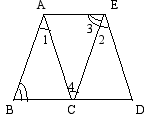
C。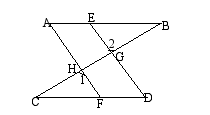 3.已知:如图,
3.已知:如图,![]() ,且B、C、D在一条直线求证:
,且B、C、D在一条直线求证:![]()
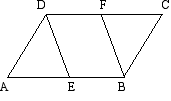 4.已知:如图,
4.已知:如图,![]() ,DE平分
,DE平分![]() ,BF平分
,BF平分![]() ,且
,且![]() 。 求证:
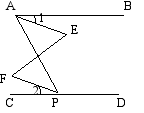
。 求证:![]() 5.已知:如图,
5.已知:如图,![]() 。 求证:
。 求证:![]()
 6.已知:如图,
6.已知:如图,![]() 。 求证:
。 求证:![]()