

初中数学沪科版七年级下册10.2 平行线的判定一等奖第1课时教案设计
展开10.2 平行线的判定
第1课时 平行线及同位角、内错角和同旁内角
![]()
【知识与技能】
1.理解平行线的意义,了解同一平面内两条直线的位置关系,会用直尺和三角板画平行线.
2.理解并掌握平行公理及其推论.
3.理解同位角、内错角、同旁内角的意义.会识别图中的同位角、内错角、同旁内角.
【过程与方法】
通过动手操作与合作交流,掌握 平行公理及其推论;通过识别同位、内错角、同旁内角培养学生的识图能力.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生观察、分析、以及推理的能力.
【教学重点】
平行公理及其推论.
【教学难点】
同位角、内错角、同旁内角的识别.
![]()
一、情境导入,初步认识
问题 在小学,我们就学过平行线和画平行线,你还记得这这些知识吗?
【教学说明】教师提出问题,学生回忆小学所学知识,激发学生继续探索.
二、思考探究,获取新知
1.平行线
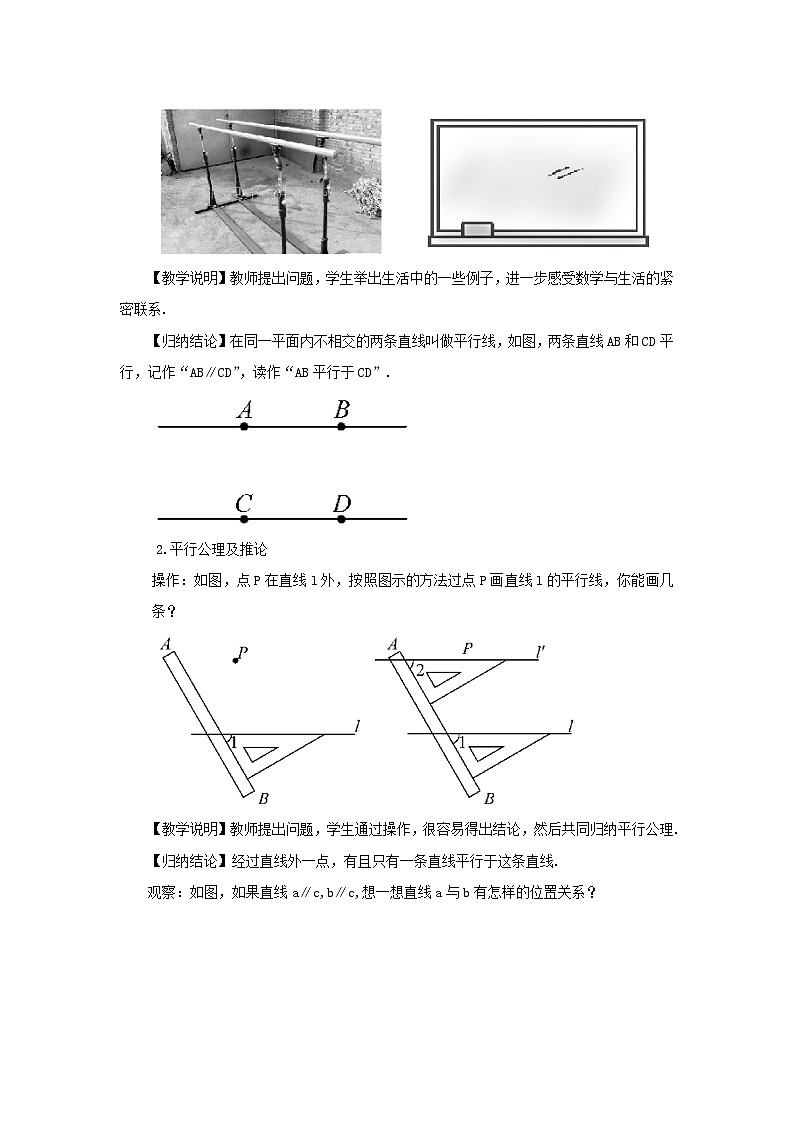
问题:如图,双杠上的两条横杠,黑板的上下两边,把它们看作直线时,都给我们平行直线的形象.你还能举出类似的例子吗?

【教学说明】教师提出问题,学生举出生活中的一些例子,进一步感受数学与生活的紧密联系.
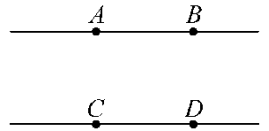
【归纳结论】在同一平面内不相交的两条直线叫做平行线,如图,两条直线AB和CD平行,记作“AB∥CD”,读作“AB平行于CD”.
2.平行公理及推论
操作:如图,点P在直线l外,按照图示的方法过点P画直线l的平行线,你能画几条?
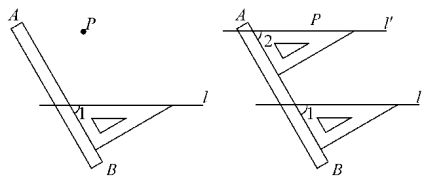
【教学说明】教师提出问题,学生通过操作,很容易得出结论,然后共同归纳平行公理.
【归纳结论】经过直线外一点,有且只有一条直线平行于这条直线.
观察:如图,如果直线a∥c,b∥c,想一想直线a与b有怎样的位置关系?

【教学说明】教师提出问题,学生通过观察,猜想a与b的位置关系,教师也可拓展,运用反证法加以证明.
【归纳结论】如果两条直线和第三条直线平行,那么这两条直线平行,即
如果直线a∥c,b∥c,那么直线a∥b.
- 同位角、内错角、同旁内角
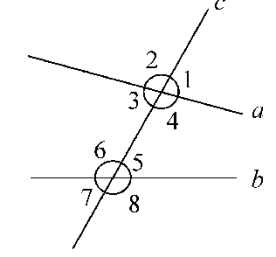
问题:如图,直线a、b被直线c所截而形成的8个角中,它们具有怎样的位置关系?
【教学说明】教师提出问题,学生独立思考,然后相互交流,发表各自的意见,通过阅读下面的文字,理解并识记同位角、内错角、同旁内角的概念.
如图,两条直线a和b被第三条直线c(相当于“基准线”)所截,其中∠1和∠5,分别在直线a和b相同的一侧,并且位于直线c的同旁,具有这样位置关系的一对角叫做同位角.
同样,∠3与∠5都在直线a和b之间,并且位于直线c的两旁,具有这样位置关系的一对角叫做内错角;∠4与∠5都在直线a和b之间,并且位于直线c的同旁,具有这样位置的一对角叫做同旁内角.
三、典例精析,掌握新知
例1如图,按下列语句画图:(1)过点A画AD∥BC;(2)过点C画CE∥AB,与AD相交于点E.
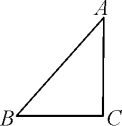
【解】如图.
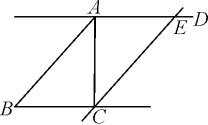
例2 如图,分别找出一个角与∠α配对,使两个角成为:(1)同位角;(2)内错角;(3)同旁内角,并指出是由哪条直线截另外两条直线而得到的.
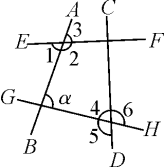
【解】(1)∠α与∠3是直线EF和GH被直线AB所截得的同位角,或∠6与∠α是直线AB和CD被直线GH所截得的同位角.
(2)∠1与∠α是直线EF和GH被直线AB所截得的内错角,或∠5与∠α是直线AB和CD被直线GH所截得的内错角.
(3)∠2与∠α是直线EF和GH被直线AB所截得的同旁内角,或∠4与∠α是直线AB和CD被直线GH所截的同旁内角.
【教学说明】教师给出例题,学生独立自主完成.教师可选几个同学上台展示自己的答案,交流各自的心得,积累解决问题的经验和方法.
四、运用新知,深化理解
1.判断题:
(1)不相交的两条直线叫做平行线.( )
(2)如果一条直线与两条平行线中的一条直线平行,那么它与另一条直线也互相平行.( )
(3)过一点有且只有一条直线平行于已知直线.( )
(4)若a与b平行,b与c平行,则a与c不相交.( )
(5)若线段AB与CD没有交点,则AB∥CD.( )
(6)在同一平面内,两条直线的位置关系有两种.( )
2.如图,直线AB,CD被直线CE所截,与∠1成内错角的是 ;与∠1成同旁内角的是 ;直线AB、CD被直线DE所截,与∠2成内错角的
是 ;与∠2成同旁内角的是 .
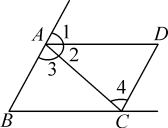
第2题图 第3题图
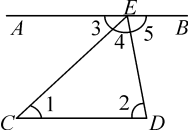
3.如图,∠1与∠D,∠1与∠B,∠3与∠4,∠B与∠BCD,∠2与∠4分别是哪两条直线被哪一条直线所截得到的?它们中的每一对角分别叫做什么角?
【教学说明】教师给出习题,学生独立自主完成.教师巡视,对有困难的学生给予点拨.
【答案】1.(1)× (2)√ (3)× (4)√ (5)× (6)√
2.∠3,∠BEC,∠5,∠AED
3.∠1与∠D是直线AB,CD被直线AD所截得的内错角;∠1与∠B是直线AD,BC被直线AB所截得的同位角;∠3与∠4是直线AB,CD被直线AC所截得的内错角;∠B与∠BCD是直线AB、CD被直线BC所截得的同旁内角;∠2与∠4是直线AD、CD被直线AC所截得的同旁内角.
五、师生互动,课堂小结
通过这节课的学习,你掌握了哪些新知识?还有哪些疑问?请与同伴交流.
【教学说明】学生相互交流,回顾平行线、同位角、内错角、同旁内角的概念和平行公理及其推论,加深对所学知识的理解和运用.
![]()
完成练习册中本课时 练习.
![]()
从生活中的实际例子引出平行线,再探究平行公理及其推论,以及同位角、内错角、同旁内角的识别,学生积极主动探究相关知识,在合作交流中体会成功的喜悦,增强学好数学的信心.
人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.3 同位角、内错角、同旁内角教学设计: 这是一份人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.3 同位角、内错角、同旁内角教学设计,共4页。教案主要包含了导学,自学,助学,强化,评价等内容,欢迎下载使用。
沪科版七年级下册10.1 相交线精品第2课时教案: 这是一份沪科版七年级下册10.1 相交线精品第2课时教案,共5页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。
湘教版第4章 相交线与平行线4.4 平行线的判定公开课第1课时教学设计: 这是一份湘教版第4章 相交线与平行线4.4 平行线的判定公开课第1课时教学设计,共5页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。













