






还剩12页未读,
继续阅读
第7章一元一次不等式与不等式组章末复习课件(沪科版七下)
展开
这是一份第7章一元一次不等式与不等式组章末复习课件(沪科版七下),共20页。
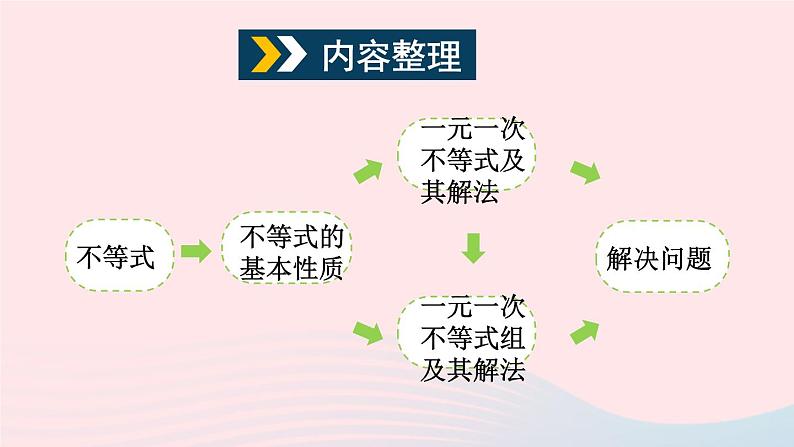
沪科版·七年级下册章末复习不等式的性质 性质 1 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变. 即 如果 a >b,那么 a + c>b + c,a – c>b – c .性质 4 如果 a > b,那么b < a.性质 5 如果 a > b,b > c,那么 a > c.解一元一次不等式的步骤解一元一次不等式组的步骤先求出不等式组中各不等式的解集;再求出这些解集的公共部分.列一元一次不等式解决实际问题的一般步骤:审:认真审题,分清已知量、未知量;找:找出题目中的不等关系,抓住关键词,如“超过”“不大于” “最多”等;设:设出适当的未知数;答:检验答案是否符合实际意义,并作答.列:根据题中不等关系,列出一元一次不等式;解:求出一元一次不等式的解集;< 2. 已知点 A(2a – 1 ,1 – 3a)在第四象限,则 a 的取值范围是 .>< 3. 解下列不等式(组),并把它们的解集在数轴上表示出来: (1)12 – 4(3x – 1)≤ 2(2x – 16);解:12 – 12x + 4 ≤ 4x – 32用数轴表示为x ≥ 3用数轴表示为解:解不等式①得:x < 0用数轴表示为解:解不等式①得:x ≤ 1.用数轴表示为解不等式②得:x < 4.所以不等式组的解集为:x ≤ 1. 4. 若不等式 3x – m ≤ 0 的正整数解是 1,2,3,则 m 的取值范围是________________.9 ≤ m < 12 5. 若代数式 的值不大于代数式 5k – 1 的值,则 k 的取值范围是 ________. 6. 如果不等式 4x – 3a > – 1 与不等式 2(x – 1)+ 3 > 5 的解集相同,请确定 a 的值. 解:解 4x – 3a > – 1 , 得 x > 3a – 14. 解 2(x – 1)+ 3 > 5, 得 x > 2. 由于两个不等式的解集相同, 7. 关于 x 的一元一次方程 4x + m + 1 = 3x – 1 的解是负数,求 m 的取值范围.解:解此方程得 x = – 2 – m ,根据方程的解是负数,可得 – 2 – m < 0,解得 m > – 2 . 8. 老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 ,一年前老张至少买了多少只种兔?解:设一年前老张买了 x 只种兔,由题意得:2 + x ≤ (2x – 1),解得 x ≥ 8.答:一年前老张至少买了 8 只种兔.
沪科版·七年级下册章末复习不等式的性质 性质 1 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变. 即 如果 a >b,那么 a + c>b + c,a – c>b – c .性质 4 如果 a > b,那么b < a.性质 5 如果 a > b,b > c,那么 a > c.解一元一次不等式的步骤解一元一次不等式组的步骤先求出不等式组中各不等式的解集;再求出这些解集的公共部分.列一元一次不等式解决实际问题的一般步骤:审:认真审题,分清已知量、未知量;找:找出题目中的不等关系,抓住关键词,如“超过”“不大于” “最多”等;设:设出适当的未知数;答:检验答案是否符合实际意义,并作答.列:根据题中不等关系,列出一元一次不等式;解:求出一元一次不等式的解集;< 2. 已知点 A(2a – 1 ,1 – 3a)在第四象限,则 a 的取值范围是 .>< 3. 解下列不等式(组),并把它们的解集在数轴上表示出来: (1)12 – 4(3x – 1)≤ 2(2x – 16);解:12 – 12x + 4 ≤ 4x – 32用数轴表示为x ≥ 3用数轴表示为解:解不等式①得:x < 0用数轴表示为解:解不等式①得:x ≤ 1.用数轴表示为解不等式②得:x < 4.所以不等式组的解集为:x ≤ 1. 4. 若不等式 3x – m ≤ 0 的正整数解是 1,2,3,则 m 的取值范围是________________.9 ≤ m < 12 5. 若代数式 的值不大于代数式 5k – 1 的值,则 k 的取值范围是 ________. 6. 如果不等式 4x – 3a > – 1 与不等式 2(x – 1)+ 3 > 5 的解集相同,请确定 a 的值. 解:解 4x – 3a > – 1 , 得 x > 3a – 14. 解 2(x – 1)+ 3 > 5, 得 x > 2. 由于两个不等式的解集相同, 7. 关于 x 的一元一次方程 4x + m + 1 = 3x – 1 的解是负数,求 m 的取值范围.解:解此方程得 x = – 2 – m ,根据方程的解是负数,可得 – 2 – m < 0,解得 m > – 2 . 8. 老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 ,一年前老张至少买了多少只种兔?解:设一年前老张买了 x 只种兔,由题意得:2 + x ≤ (2x – 1),解得 x ≥ 8.答:一年前老张至少买了 8 只种兔.
相关资料
更多









