


广东省陆丰市民声学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案
展开
这是一份广东省陆丰市民声学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了点位于平面直角坐标系中的.,已知反比例函数图像经过点等内容,欢迎下载使用。
广东省陆丰市民声学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AD、AB边上的中点,连接EF,若EF=![]() ,OC=2,则菱形ABCD的面积为( )
,OC=2,则菱形ABCD的面积为( )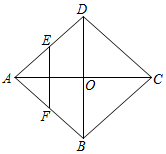 A.2
A.2![]() B.4
B.4![]() C.6
C.6![]() D.8
D.8![]() 2.关于正比例函数y=﹣3x,下列结论正确的是( )A.图象不经过原点 B.y随x的增大而增大C.图象经过第二、四象限 D.当x=
2.关于正比例函数y=﹣3x,下列结论正确的是( )A.图象不经过原点 B.y随x的增大而增大C.图象经过第二、四象限 D.当x=![]() 时,y=13.若m个数的平均数x,另n个数的平均数y,则m+n个数的平均数是( )A.
时,y=13.若m个数的平均数x,另n个数的平均数y,则m+n个数的平均数是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.点
4.点![]() 位于平面直角坐标系中的( ).A.第一象限 B.第二象限 C.第三象限 D.第四象限5.如图,阴影部分为一个正方形,此正方形的面积是( )\
位于平面直角坐标系中的( ).A.第一象限 B.第二象限 C.第三象限 D.第四象限5.如图,阴影部分为一个正方形,此正方形的面积是( )\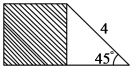 A.2 B.4 C.6 D.86.已知反比例函数
A.2 B.4 C.6 D.86.已知反比例函数![]() 图像经过点(2,—3),则下列点中必在此函数图像上的是( )A.(2, 3) B.(1, 6) C.(—1, 6) D.(—2,—3)7.若二次根式
图像经过点(2,—3),则下列点中必在此函数图像上的是( )A.(2, 3) B.(1, 6) C.(—1, 6) D.(—2,—3)7.若二次根式![]() 在实数范围内有意义,则a的取值范围是( )A.
在实数范围内有意义,则a的取值范围是( )A.![]() B.
B.![]() C.a>1 D.a<18.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是
C.a>1 D.a<18.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是![]() A.6cm B.5cm C.
A.6cm B.5cm C.![]() D.
D.![]() 9.已知菱形的边长和一条对角线的长均为2 cm,则菱形的面积为( )A.3cm2 B.4 cm2 C.
9.已知菱形的边长和一条对角线的长均为2 cm,则菱形的面积为( )A.3cm2 B.4 cm2 C.![]() cm2 D.2
cm2 D.2![]() cm210.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组
cm210.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组![]() 的解是( )
的解是( )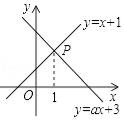 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.下列语句描述的事件中,是不可能事件的是( )A.只手遮天,偷天换日 B.心想事成,万事如意C.瓜熟蒂落,水到渠成 D.水能载舟,亦能覆舟12.下列各式:
11.下列语句描述的事件中,是不可能事件的是( )A.只手遮天,偷天换日 B.心想事成,万事如意C.瓜熟蒂落,水到渠成 D.水能载舟,亦能覆舟12.下列各式:![]() ,
,![]() ,
,![]() +y,
+y,![]() ,
,![]() ,其中分式共有( )A.1个 B.2个 C.3个 D.4个二、填空题(每题4分,满分20分,将答案填在答题纸上)13.以正方形ABCD一边AB为边作等边三角形ABE,则∠CED=_____.14.使式子
,其中分式共有( )A.1个 B.2个 C.3个 D.4个二、填空题(每题4分,满分20分,将答案填在答题纸上)13.以正方形ABCD一边AB为边作等边三角形ABE,则∠CED=_____.14.使式子![]() 的值为0,则a的值为_______.15.化简:
的值为0,则a的值为_______.15.化简:![]() ___________.16.已知方程
___________.16.已知方程![]() 的一个根为2,则
的一个根为2,则![]() ________.17.一组数据x1,x2,…,xn的平均数是2,方差为1,则3x1,3x2,…,3xn,的方差是_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.试探究下列问题:
________.17.一组数据x1,x2,…,xn的平均数是2,方差为1,则3x1,3x2,…,3xn,的方差是_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.试探究下列问题: (1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论. 19.(5分)如图,▱ABCD中,
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论. 19.(5分)如图,▱ABCD中,![]() ,
,![]() ,垂足分别是E,
,垂足分别是E,![]() 求证:
求证:![]() .
.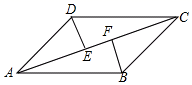 20.(8分)已知一个三角形的三边长分别为
20.(8分)已知一个三角形的三边长分别为![]() ,求这个三角形的周长(要求结果化简). 21.(10分)如图1,在
,求这个三角形的周长(要求结果化简). 21.(10分)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以OB为边,在
,以OB为边,在![]() 外作等边
外作等边![]() ,D是OB的中点,连接AD并延长交OC于E.
,D是OB的中点,连接AD并延长交OC于E.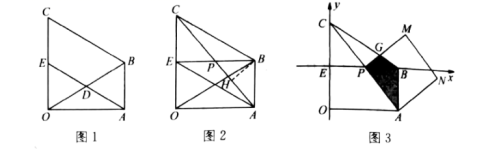 (1)求证:四边形ABCE是平行四边形;(2)连接AC,BE交于点P,求AP的长及AP边上的高BH;(3)在(2)的条件下,将四边形OABC置于如图所示的平面直角坐标系中,以E为坐标原点,其余条件不变,以AP为边向右上方作正方形APMN:①M点的坐标为 . ②直接写出正方形APMN与四边形OABC重叠部分的面积(图中阴影部分). 22.(10分)电话计费问题,下表中有两种移动电话计费方式:
(1)求证:四边形ABCE是平行四边形;(2)连接AC,BE交于点P,求AP的长及AP边上的高BH;(3)在(2)的条件下,将四边形OABC置于如图所示的平面直角坐标系中,以E为坐标原点,其余条件不变,以AP为边向右上方作正方形APMN:①M点的坐标为 . ②直接写出正方形APMN与四边形OABC重叠部分的面积(图中阴影部分). 22.(10分)电话计费问题,下表中有两种移动电话计费方式: 温馨揭示:方式一:月使用费固定收(月收费:38元/月);主叫不超限定时间不再收费(80分钟以内,包括80分钟);主叫超时部分加收超时费(超过部分0.15元/
温馨揭示:方式一:月使用费固定收(月收费:38元/月);主叫不超限定时间不再收费(80分钟以内,包括80分钟);主叫超时部分加收超时费(超过部分0.15元/![]() );被叫免费。方式二:月使用费0元(无月租费);主叫限定时间0分钟;主叫每分钟0.35元/
);被叫免费。方式二:月使用费0元(无月租费);主叫限定时间0分钟;主叫每分钟0.35元/![]() ;被叫免费。(1)设一个月内用移动电话主叫时间为
;被叫免费。(1)设一个月内用移动电话主叫时间为![]() ,方式一计费
,方式一计费![]() 元,方式二计费
元,方式二计费![]() 元。写出
元。写出![]() 和
和![]() 关于
关于![]() 的函数关系式。(2)在平面直角坐标系中画出(1)中的两个函数图象,记两函数图象交点为点
的函数关系式。(2)在平面直角坐标系中画出(1)中的两个函数图象,记两函数图象交点为点![]() ,则点
,则点![]() 的坐标为_____________________(直接写出坐标,并在图中标出点
的坐标为_____________________(直接写出坐标,并在图中标出点![]() )。(3)根据(2)中函数图象,请直接写出如何根据每月主叫时间选择省钱的计费方式。
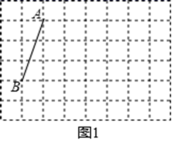
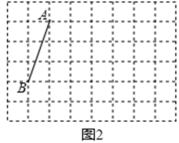
)。(3)根据(2)中函数图象,请直接写出如何根据每月主叫时间选择省钱的计费方式。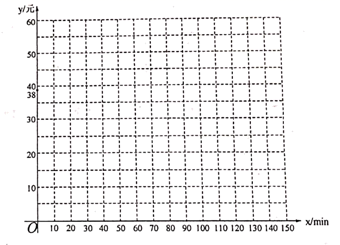 23.(12分)如图,方格纸中每个小正方形的边长均为1,我们把每个小正方形的顶点叫做格点. 如:线段AB的两个端点都在格点上.(1)在图1中画一个以AB为边的平行四边形ABCD,点C、D在格点上,且平行四边形ABCD的面积为15;(2)在图2中画一个以AB为边的菱形ABEF(不是正方形),点E、F在格点上,则菱形ABEF的对角线AE=________,BF=________;(3)在图3中画一个以AB为边的矩形ABMN(不是正方形),点M、N在格点上,则矩形ABMN的长宽比
23.(12分)如图,方格纸中每个小正方形的边长均为1,我们把每个小正方形的顶点叫做格点. 如:线段AB的两个端点都在格点上.(1)在图1中画一个以AB为边的平行四边形ABCD,点C、D在格点上,且平行四边形ABCD的面积为15;(2)在图2中画一个以AB为边的菱形ABEF(不是正方形),点E、F在格点上,则菱形ABEF的对角线AE=________,BF=________;(3)在图3中画一个以AB为边的矩形ABMN(不是正方形),点M、N在格点上,则矩形ABMN的长宽比![]() =______.
=______. 
 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、C4、A5、D6、C7、A8、B9、D10、A11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、30°或150°.14、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、C4、A5、D6、C7、A8、B9、D10、A11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、30°或150°.14、![]() 15、
15、![]() 16、
16、![]() 17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.19、证明见解析.20、
17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.19、证明见解析.20、![]() .21、(1)见解析;(2)
.21、(1)见解析;(2)![]() ,
,![]() ;(3)①
;(3)①![]() ;②
;②![]() 22、(1)当
22、(1)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ,见解析;(3)当每月主叫时间小于130分钟时选择方式二省钱;当每月主叫时间等于130分钟时两种方式都一样;当每月主叫时间大于130分钟时选择方式一省钱.23、(1)答案见详解;(1)
,见解析;(3)当每月主叫时间小于130分钟时选择方式二省钱;当每月主叫时间等于130分钟时两种方式都一样;当每月主叫时间大于130分钟时选择方式一省钱.23、(1)答案见详解;(1)![]() ,
,![]() ;(3)1.
;(3)1.
相关试卷
这是一份2023-2024学年广东省汕尾陆丰市九年级数学第一学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了已知函数是的图像过点,则的值为等内容,欢迎下载使用。
这是一份广东省陆丰市民声学校2023-2024学年数学九年级第一学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,函数y=3,若是方程的两根,则的值是等内容,欢迎下载使用。
这是一份广东省陆丰市民声学校2023-2024学年八上数学期末学业水平测试试题含答案,共6页。试卷主要包含了下列命题中,是假命题的是,下列命题属于真命题的是等内容,欢迎下载使用。








