广东省茂名市直属学校2022-2023学年数学七下期末综合测试试题含答案

这是一份广东省茂名市直属学校2022-2023学年数学七下期末综合测试试题含答案，共7页。试卷主要包含了下列命题正确的是等内容，欢迎下载使用。
广东省茂名市直属学校2022-2023学年数学七下期末综合测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．如图所示，下列结论中不正确的是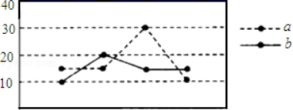（  ）A．a组数据的最大数与最小数的差较大 B．a组数据的方差较大C．b组数据比较稳定 D．b组数据的方差较大2．下列是最简二次根式的为（　　）A． B． C． D．（a＞0）3．如图，已知一条直线经过点、点，将这条直线向左平移与轴、轴分别交于点、点．若，则直线的函数解析式为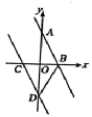（　　）A． B． C． D．4．若代数式有意义，则实数x的取值范围是A．    B．    C．    D．且5．某青年排球队12名队员的年龄情况如下表所示：这12名队员的平均年龄是（    ）A．18岁 B．19岁 C．20岁 D．21岁6．甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2如下表所示： 甲乙丙丁平均数（cm）561560561560方差s23.53.515.516.5根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（　　）A．甲 B．乙 C．丙 D．丁7．一个多边形的每个内角均为120°，则这个多边形是（   ）A．四边形 B．五边形 C．六边形 D．七边形8．下列命题正确的是(   )A．在同一平面内，可以把半径相等的两个圆中的一个看成是由另一个平移得到的.B．两个全等的图形之间必有平移关系.C．三角形经过旋转，对应线段平行且相等.D．将一个封闭图形旋转，旋转中心只能在图形内部.9．已知函数y=kx-k的图象如图所示，则k的取值为(　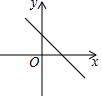　)A．k＜0 B．k＞0 C．k≥0 D．k≤010．已知长方形的周长为16cm，其中一边长为xcm，面积为ycm2，则这个长方形的面积y与边长x之间的关系可表示为(    )A．y＝x2 B．y＝(8﹣x)2 C．y＝x(8﹣x) D．y＝2(8﹣x)11．下列各组数中能作为直角三角形的三边长的是（　　）．A．1，，1 B．2，3，4 C．4，5，6 D．8，13，512．已知y与（x﹣1）成正比例，当x＝1时，y＝﹣1．则当x＝3时，y的值为（  ）A．1 B．﹣1 C．3 D．﹣3二、填空题（每题4分，满分20分，将答案填在答题纸上）13．若正多边形的一个外角等于36°，那么这个正多边形的边数是________．14．甲、乙两人进行射击测试，每人10次射击成绩的平均数都是8.5环，方差分别是：S甲2=2，S乙2=1.5，则射击成绩较稳定的是_____________（填“甲”或“乙“）．15．如图，平行四边形ABCD中，∠A的平分线AE交CD于E，连接BE，点F、G分别是BE、BC的中点，若AB=6，BC=4，则FG的长_________________.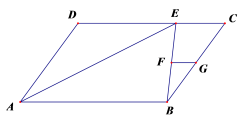16．若实数x，y满足＋(y＋)2＝0，则yx的值为________.17．如图，P是反比例函数图象上的一点，轴于A，点B，C在y轴上，四边形PABC是平行四边形，则▱PABC的面积是______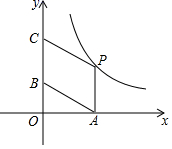．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）一辆货车从A地运货到240km的B地，卸货后返回A地，如图中实线是货车离A地的路程y（km）关于出发后的时间x（h）之间的函数图象．货车出发时，正有一个自行车骑行团在AB之间，距A地40km处，以每小时20km的速度奔向B地．（1）货车去B地的速度是　        　，卸货用了　 　小时，返回的速度是　     　；（2）求出自行车骑行团距A地的路程y（km）关于x的函数关系式，并在此坐标系中画出它的图象；（3）求自行车骑行团与货车迎面相遇，是货车出发后几小时后，自行车骑行团还有多远到达B地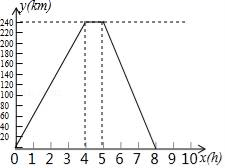．   19．（5分）我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．（1）若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．   20．（8分）（1）；（2）÷   21．（10分）某汽车制造厂开发了一款新式电动汽车，计划一年生产安装240辆．由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装．生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车．(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车？(2)如果工厂招聘新工人若干名(新工人人数少于10人)和抽调的熟练工合作,刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?   22．（10分）下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.已知:如图，在RtΔABC中，∠ABC=90°，0为AC的中点.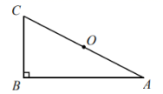求作:四边形ABCD，使得四边形ABCD为矩形.作法:①作射线BO，在线段BO的延长线上取点D，使得DO=BO；②连接AD，CD，则四边形ABCD为矩形.根据小丁设计的尺规作图过程.(1)使用直尺和圆规，在图中补全图形(保留作图痕迹)；(2)完成下面的证明.证明:∴点O为AC的中点，∴AO=CO.又∵DO=BO，∵四边形ABCD为平行四边形(__________)(填推理的依据).∵∠ABC=90°，∴ABCD为矩形(_________)(填推理的依据).   23．（12分）如图，在中，，点在上，若，平分. （1）求的长；（2）若是中点，求线段的长. 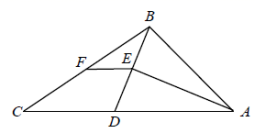   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、D2、A3、A4、D5、C6、A7、C8、A9、A10、C11、A12、A 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、十14、乙15、116、317、6 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）60km/h，1小时，80km/h（2）y=20x+40 （0≤x≤10）（3）自行车骑行团与货车迎面相遇，是货车出发后6小时后，自行车骑行团还有80km到达B地19、（1）购买甲种树苗500株，乙种树苗300株（2）320株（3）当选购甲种树苗320株，乙种树苗480株时，总费用最低，为22080元20、 (1) -45;(2) 2+4.21、（1）每名熟练工每月可以安装4辆电动车，新工人每月分别安装2辆电动汽车.（2） ①调熟练工1人，新工人8人；②调熟练工2人，新工人6人；③调熟练工3人，新工人4人；④调熟练工4人，新工人2人．22、 (1)作图如图所示，见解析(2)对角线互相平分的四边形是平行四边形， 有一个角是直角的平行四边形是矩形.23、 (1)12;(2)5