广东省阳江市江城区2022-2023学年七年级数学第二学期期末监测模拟试题含答案

这是一份广东省阳江市江城区2022-2023学年七年级数学第二学期期末监测模拟试题含答案，共7页。试卷主要包含了如果，那么等于等内容，欢迎下载使用。
广东省阳江市江城区2022-2023学年七年级数学第二学期期末监测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．方差是表示一组数据的A．变化范围 B．平均水平 C．数据个数 D．波动大小2．若，是函数图象上的两点，当时，下列结论正确的是　　A． B． C． D．3．下列结论中，正确的是（　　）A．四边相等的四边形是正方形B．对角线相等的菱形是正方形C．正方形两条对角线相等，但不互相垂直平分D．矩形、菱形、正方形都具有“对角线相等”的性质4．如果，那么等于A．3:2 B．2:5 C．5:3 D．3:55．在平面直角坐标系中，若直线y＝2x+k经过第一、二、三象限，则k的取值范围是（　　）A．k＞0 B．k＜0 C．k≤0 D．k≥06．已知a＜b，则下列不等式正确的是（　　）A．a﹣3＜b﹣3 B．＞ C．﹣a＜﹣b D．6a＞6b7．已知实数，在数轴上的位置如图所示，化简：的结果是(   )A． B．C． D．8．在ABCD中，∠A＝40°，则∠C＝(　　)A．40° B．50° C．130° D．140°9．在平面直角坐标系中，点P(2，－3)关于原点对称的点的坐标是(   )A．(2，3)    B．(－2，3)    C．(－2，－3)    D．(－3，2)10．如图，直线y＝x+b与直线y＝kx+7交于点P（3，5），通过观察图象我们可以得到关于x的不等式x+b＞kx+7的解集为x＞3，这一求解过程主要体现的数学思想是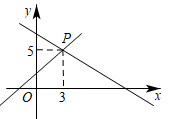（　　）A．分类讨论 B．类比 C．数形结合 D．公理化二、填空题(本大题共有6小题，每小题3分，共18分)11．在菱形ABCD中，两条对角线AC与BD的和是1．菱形的边AB＝5，则菱形ABCD的面积是_____．12． “五一”期间，小红到某景区登山游玩，小红上山时间x（分钟）与走过的路程y（米）之间的函数关系如图所示，在小红出发的同时另一名游客小卉正在距离山底60米处沿相同线路上山，若小红上山过程中与小卉恰好有两次相遇，则小卉上山平均速度v（米/分钟）的取值范围是_____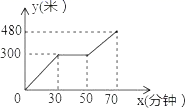．13．若方程组的解是，则直线y＝﹣2x+b与直线y＝x﹣a的交点坐标是_____．14．据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根，华罗庚脱口而出：1．你知道他是怎么快速准确地计算出来的吗？请研究解决下列问题：已知x3＝10648，且x为整数∵1000＝103＜10648＜1003＝1000000，∴x一定是______位数∵10648的个位数字是8，∴x的个位数字一定是______；划去10648后面的三位648得10，∵8＝23＜10＜33＝27，∴x的十位数字一定是_____；∴x＝______.15．某校对1200名学生的身高进行了测量，身高在1.58～1.63（单位：）这一个小组的频率为0.25，则该组的人数是________.16．将直线的图象向上平移3个单位长度，得到直线______．三、解下列各题(本大题共8小题，共72分)17．（8分）已知一次函数的图象经过点(3,4)与(-3,-8).(1)求这个一次函数的解析式；(2)求关于的不等式的解集.   18．（8分）当今，青少年用电脑手机过多，视力水平下降已引起了全社会的关注，某校为了解八年级1000名学生的视力情况，从中抽查了150名学生的视力情况，通过数据处理，得到如下的频数分布表．解答下列问题：视力范围分组组中值频数3.95≤x＜4.254.1204.25≤x＜4.554.4104.55≤x＜4.854.7304.85≤x＜5.155.0605.15≤x＜5.455.330合计 150（1）分别指出参加抽测学生的视力的众数、中位数所在的范围；（2）若视力为4.85以上（含4.85）为正常，试估计该校八年级学生视力正常的人数约为多少？（3）根据频数分布表求加权平均数时，统计中常用各组的组中值代表各组的实际数据，把各组的频数相应组中的权．请你估计该校八年级学生的平均视力是多少？   19．（8分）某服装公司招工广告承诺：熟练工人每月工资至少4000元．每天工作8小时，一个月工作25天．月工资底薪1000元，另加计件工资．加工1件A型服装计酬20元，加工1件B型服装计酬15元．在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时，加工1件A型服装和2件B型服装需4小时．(工人月工资＝底薪+计件工资)(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时？(2)一段时间后，公司规定：“每名工人每月必须加工A，B两种型号的服装，且加工A型服装数量不少于B型服装的一半”．设一名熟练工人每月加工A型服装a件，工资总额为W元．请你运用所学知识判断该公司在执行规定后是否违背了广告承诺？   20．（8分）如图，A，B，C，D为四家超市，其中超市D距A，B，C三家超市的路程分别为25km，10km，5km．现计划在A，D之间的道路上建一个配货中心P，为避免交通拥堵，配货中心与超市之间的距离不少于2km．假设一辆货车每天从P出发为这四家超市送货各1次，由于货车每次仅能给一家超市送货，因此每次送货后均要返回配货中心P，重新装货后再前往其他超市．设P到A的路程为xkm，这辆货车每天行驶的路程为ykm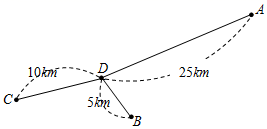．（1）求y与x之间的函数关系式，并写出自变量x的取值范围；（2）直接写出配货中心P建在什么位置，这辆货车每天行驶的路程最短？最短路程是多少？   21．（8分）两个含有二次根式的代数式相乘，积不含有二次根式，称这两个代数式互为有理化因式，例如: 与、与等都是互为有理化因式，在进行二次根式计算时，利用有理化因式，可以化去分母中的根号.例如: ；；…….请仿照上述过程，化去下列各式分母中的根号. (1) (2) (n为正整数).   22．（10分）对于实数a，b，定义运算“*”，a*b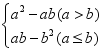＝例如4*1．因为4＞1，所以4*1＝41－4×1＝8，若x1、x1是一元二次方程x1－9x＋10＝0的两个根，则x1*x1＝__．   23．（10分）如图，在平面直角坐标系中，为坐标原点，矩形的顶点，将矩形的一个角沿直线 折叠，使得点 落在对角线 上的点 处，折痕与 轴交于点 .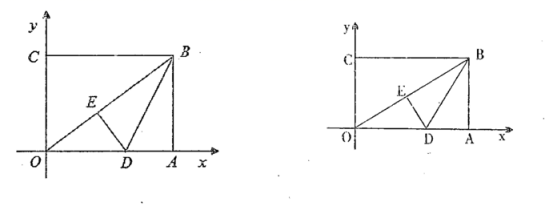（1）求直线所对应的函数表达式；（2）若点 在线段上，在线段 上是否存在点 ，使以 为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由.   24．（12分）随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业，据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座。（1）计划到2020年底，全省5G基站的数量是多少万座？；（2）按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率。   参考答案 一、选择题(每小题3分,共30分)1、D2、A3、B4、B5、A6、A7、B8、A9、B10、C 二、填空题(本大题共有6小题，每小题3分，共18分)11、212、6＜v＜2或v＝4.213、（-1，3）14、两；2；2；2215、1．16、 三、解下列各题(本大题共8小题，共72分)17、（1）y=2x−2；（2）x⩽1.18、（1）众数在4.85≤x＜5.15的范围内，中位数在4.85≤x＜5.15的范围内；（2）八年级视力正常的学生约有600人；（3）八年级1000名学生平均视力为4.1．19、 (1)一名熟练工加工1件A型服装和1件B型服装各需要2小时和1小时；(2)该服装公司执行规定后违背了广告承诺．20、（1）y═-4x+180（2≤x≤23）；（2）当配货中心P建在AP=23km位置时，这辆货车每天行驶的路程最短．其最短路程是88km．21、（1）；（2）.22、423、（1）y=2x-1；（2）存在点，Q（，）， 使以为顶点的四边形为平行四边形.24、（1）到2020年底，全省5G基站的数量是6万座；（2）2020年底到2022年底，全省5G基站数量的年平均增长率为.