人教版九年级上册22.2二次函数与一元二次方程课后复习题

这是一份人教版九年级上册22.2二次函数与一元二次方程课后复习题，共4页。试卷主要包含了能力提升，创新应用等内容，欢迎下载使用。
22.2　二次函数与一元二次方程一、能力提升1.若函数y=x2-2x+b的图象与坐标轴有三个交点,则b的取值范围是(　　)A.b<1,且b≠0 B.b>1C.0<b<1 D.b<12.根据下列表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解x的取值范围是(　　)x6.176.186.196.20ax2+bx+c-0.03-0.010.020.04A.6<x<6.17 B.6.17<x<6.18C.6.18<x<6.19 D.6.19<x<6.203.如图,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(3,0),与y轴交于点C.下列结论: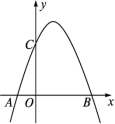①ac>0;②当x>0时,y随x的增大而增大;③3a+c=0;④a+b≥am2+bm.其中正确的个数有(　　)A.1个 B.2个 C.3个 D.4个4.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,-2),点A(-1,m)在抛物线上,则下列结论错误的是(　　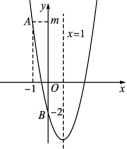)A.ab<0B.一元二次方程ax2+bx+c=0的正实数根在2和3之间C.a=D.若点P1(t,y1),P2(t+1,y2)在抛物线上,则当实数t>时,y1<y25.在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac.设函数y1,y2,y3的图象与x轴的交点个数分别为M1,M2,M3,(　　)A.若M1=2,M2=2,则M3=0B.若M1=1,M2=0,则M3=0C.若M1=0,M2=2,则M3=0D.若M1=0,M2=0,则M3=06.已知二次函数的图象如图,则: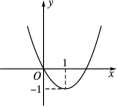(1)这个二次函数的解析式为　; (2)当x=　　　　　时,y=3; (3)根据图象回答:当x　　　　　　　　　　时,y>0;当x　　　　　　　　　　时,y<0. 7.抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是　　　　　. 8.已知抛物线y=mx2+(3-2m)x+m-2(m≠0)与x轴有两个不同的交点.(1)求m的取值范围;(2)判断点P(1,1)是否在抛物线上;(3)当m=1时,求抛物线的顶点Q及点P(1,1)关于抛物线的对称轴对称的点P'的坐标.   9.已知抛物线y=ax2-2ax-8(a≠0)经过点(-2,0).(1)求抛物线的函数解析式和顶点坐标.(2)直线l交抛物线于点A(-4,m),B(n,7),n为正数.若点P在抛物线上且在直线l下方(不与点A,B重合),分别求出点P横坐标与纵坐标的取值范围.  ★10.设二次函数y=ax2+bx-(a+b)(a,b是常数,a≠0).(1)判断该二次函数图象与x轴的交点的个数,说明理由;(2)若该二次函数图象经过A(-1,4),B(0,-1),C(1,1)三个点中的其中两个点,求该二次函数的解析式;(3)若a+b<0,点P(2,m)(m>0)在该二次函数图象上,求证:a>0.  二、创新应用★11.已知二次函数y=ax2+bx+c的图象过点A(2,0),且与函数y=-x+3的图象相交于B,C两点,点B在x轴上,点C在y轴上.(1)求该二次函数的解析式.(2)如果P(x,y)是线段BC上的动点,O为坐标原点,试求△AOP的面积S△AOP与x之间的函数解析式,并求自变量x的取值范围.(3)是否存在这样的点P,使PO=AO?若存在,求出点P的坐标;若不存在,请说明理由.
一、能力提升1.A　∵函数y=x2-2x+b的图象与坐标轴有三个交点,∴解得b<1,且b≠0.故选A.2.C　3.B　4.D　5.B6.(1)y=(x-1)2-1　(2)-1或3　(3)小于0或大于2　大于0且小于27.28.解(1)由题意可知抛物线对应的一元二次方程的判别式Δ>0,且m≠0,即b2-4ac=(3-2m)2-4m(m-2)>0,且m≠0,解得m<,且m≠0.(2)当x=1时,由题意得m+(3-2m)+m-2=1,符合函数解析式,所以点P(1,1)在抛物线上.(3)因为m=1,所以y=x2+x-1=.所以Q.根据对称性可得P'(-2,1).9.解把(-2,0)代入y=ax2-2ax-8,得0=4a+4a-8,解得a=1,∴抛物线的函数解析式为y=x2-2x-8.∵y=x2-2x-8=(x-1)2-9,∴抛物线的顶点坐标为(1,-9).(2)把x=-4代入y=x2-2x-8,得y=(-4)2-2×(-4)-8=16,∴m=16.把y=7代入函数解析式,得7=n2-2n-8,解得n=5或n=-3.∵n为正数,∴n=5.∴点A的坐标为(-4,16),点B的坐标为(5,7).∵抛物线开口向上,顶点坐标为(1,-9),∴抛物线的顶点在AB下方,∴-4<xP<5,-9≤yP<16.10.(1)解∵Δ=b2-4a[-(a+b)]=b2+4ab+4a2=(2a+b)2≥0,∴二次函数图象与x轴的交点的个数为两个或一个.(2)解∵当x=1时,y=a+b-(a+b)=0,∴抛物线y=ax2+bx-(a+b)不经过点C.把点A(-1,4),B(0,-1)的坐标分别代入y=ax2+bx-(a+b),得解得∴抛物线解析式为y=3x2-2x-1.(3)证明当x=2时,m=4a+2b-(a+b)=3a+b>0, ①∵a+b<0,∴-a-b>0. ②①②相加,得2a>0,∴a>0.二、创新应用11.解(1)由题意可知,函数y=-x+3的图象与x轴交于点B(4,0),与y轴交于点C(0,3).所以c=3.把A(2,0),B(4,0)代入y=ax2+bx+3,得解得所以所求函数的解析式为y=x2-x+3.(2)如图所示,S△AOP=OA·y=×2·y=y=-x+3(0≤x<4).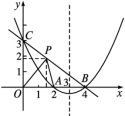(3)不存在这样的点P,使PO=AO.理由:设存在这样的点P(x0,y0),满足PO=AO,则PO=2.如图,PO=,所以=4.又因为y0=-x0+3,所以25-72x0+80=0.因为b2-4ac=(-72)2-4×25×80=-2816<0,所以此一元二次方程无解.故不存在这样的点P,使PO=AO.