


惠州市第五中学2022-2023学年七下数学期末质量跟踪监视试题含答案
展开
这是一份惠州市第五中学2022-2023学年七下数学期末质量跟踪监视试题含答案,共6页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
惠州市第五中学2022-2023学年七下数学期末质量跟踪监视试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列因式分解正确的是( )A.x3﹣x=x(x2﹣1) B.﹣a2+6a﹣9=﹣(a﹣3)2C.x2+y2=(x+y)2 D.a3﹣2a2+a=a(a+1)(a﹣1)2.同一平面直角坐标系中,一次函数![]() 与
与![]() (
(![]() 为常数)的图象可能是A.
为常数)的图象可能是A.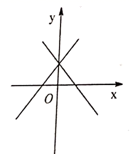 B.
B. C.
C.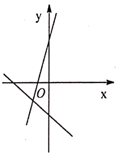 D.
D.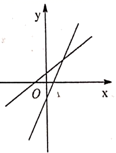 3.下列说法中,正确的是( )A.有两边相等的平行四边形是菱形B.两条对角线互相垂直平分的四边形是菱形C.两条对角线相等且互相平分的四边形是菱形D.四个角相等的四边形是菱形4.如图,在△ABC中,AB=3,BC=6,AC=4,点D,E分别是边AB,CB的中点,那么DE的长为( )
3.下列说法中,正确的是( )A.有两边相等的平行四边形是菱形B.两条对角线互相垂直平分的四边形是菱形C.两条对角线相等且互相平分的四边形是菱形D.四个角相等的四边形是菱形4.如图,在△ABC中,AB=3,BC=6,AC=4,点D,E分别是边AB,CB的中点,那么DE的长为( )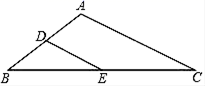 A.1.5 B.2 C.3 D.45.在平面直角坐标系中,点M(﹣2,1)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限6.某班5位学生参加中考体育测试的成绩(单位:分)分别是:50、45、36、48、50,则这组数据的众数是( )A.36 B.45 C.48 D.507.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( )A.29人 B.30人 C.31人 D.32人8.关于二次函数y=﹣2x2+1,以下说法正确的是( )A.开口方向向上 B.顶点坐标是(﹣2,1)C.当x<0时,y随x的增大而增大 D.当x=0时,y有最大值﹣
A.1.5 B.2 C.3 D.45.在平面直角坐标系中,点M(﹣2,1)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限6.某班5位学生参加中考体育测试的成绩(单位:分)分别是:50、45、36、48、50,则这组数据的众数是( )A.36 B.45 C.48 D.507.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( )A.29人 B.30人 C.31人 D.32人8.关于二次函数y=﹣2x2+1,以下说法正确的是( )A.开口方向向上 B.顶点坐标是(﹣2,1)C.当x<0时,y随x的增大而增大 D.当x=0时,y有最大值﹣![]() 9.函数y=
9.函数y=![]() 中,自变量x的取值范围是( )A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠210.如图,直线
中,自变量x的取值范围是( )A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠210.如图,直线![]() 过点
过点![]() 和点
和点![]() ,则方程
,则方程![]() 的解是( )
的解是( )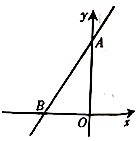 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.为了考察甲、乙、丙3种小麦的苗高,分别从中随机各抽取了100株麦苗,测得数据,并计算其方差分别是:S2甲=1.4,S2乙=18.8,S2丙=2.5,则苗高比较整齐的是( )A.甲种 B.乙种 C.丙种 D.无法确定12.二次根式
11.为了考察甲、乙、丙3种小麦的苗高,分别从中随机各抽取了100株麦苗,测得数据,并计算其方差分别是:S2甲=1.4,S2乙=18.8,S2丙=2.5,则苗高比较整齐的是( )A.甲种 B.乙种 C.丙种 D.无法确定12.二次根式![]() 中x的取值范围是( )A.x≥5 B.x≤5 C.x≥﹣5 D.x<5二、填空题(每题4分,满分20分,将答案填在答题纸上)13.计算:
中x的取值范围是( )A.x≥5 B.x≤5 C.x≥﹣5 D.x<5二、填空题(每题4分,满分20分,将答案填在答题纸上)13.计算:![]() =_______.14.如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为
=_______.14.如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为![]() ,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)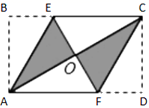 15.函数y=kx与y=6–x的图像如图所示,则k=________.
15.函数y=kx与y=6–x的图像如图所示,则k=________.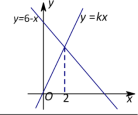 16.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.17.如果将直线
16.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.17.如果将直线![]() 平移,使其经过点
平移,使其经过点![]() ,那么平移后所得直线的表达式是__________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在
,那么平移后所得直线的表达式是__________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在![]() 中,点
中,点![]() 是
是![]() 边的一个动点,过点
边的一个动点,过点![]() 作
作![]() ,交
,交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,
, (1)求证:
(1)求证:![]() ;(2)当点
;(2)当点![]() 位于
位于![]() 边的什么位置时四边形
边的什么位置时四边形![]() 是矩形?并说明理由. 19.(5分)如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD. (1)求证:△COD 是等边三角形.(2)求∠OAD 的度数. (3)探究:当α为多少度时,△AOD 是等腰三角形?
是矩形?并说明理由. 19.(5分)如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD. (1)求证:△COD 是等边三角形.(2)求∠OAD 的度数. (3)探究:当α为多少度时,△AOD 是等腰三角形? 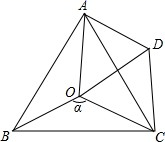 20.(8分)为了了解高峰时段37路公交车从总站乘该路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:16,25,18,1,25,30,28,29,25,1.(1)请求出这10个班次乘该路车人数的平均数、众数与中位数; (2)如果37路公交车在高峰时段从总站共发出50个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人? 21.(10分)已知,在菱形ABCD中,G是射线BC上的一动点(不与点B,C重合),连接AG,点E、F是AG上两点,连接DE,BF,且知∠ABF=∠AGB,∠AED=∠ABC.
20.(8分)为了了解高峰时段37路公交车从总站乘该路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:16,25,18,1,25,30,28,29,25,1.(1)请求出这10个班次乘该路车人数的平均数、众数与中位数; (2)如果37路公交车在高峰时段从总站共发出50个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人? 21.(10分)已知,在菱形ABCD中,G是射线BC上的一动点(不与点B,C重合),连接AG,点E、F是AG上两点,连接DE,BF,且知∠ABF=∠AGB,∠AED=∠ABC.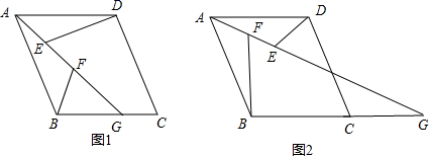 (1)若点G在边BC上,如图1,则:①△ADE与△BAF______;(填“全等”或“不全等”或“不一定全等”)②线段DE、BF、EF之间的数量关系是______;(2)若点G在边BC的延长线上,如图2,那么上面(1)②探究的结论还成立吗?如果成立,请给出证明;如果不成立,请说明这三条线段之间又怎样的数量关系,并给出你的证明. 22.(10分)中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
(1)若点G在边BC上,如图1,则:①△ADE与△BAF______;(填“全等”或“不全等”或“不一定全等”)②线段DE、BF、EF之间的数量关系是______;(2)若点G在边BC的延长线上,如图2,那么上面(1)②探究的结论还成立吗?如果成立,请给出证明;如果不成立,请说明这三条线段之间又怎样的数量关系,并给出你的证明. 22.(10分)中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图: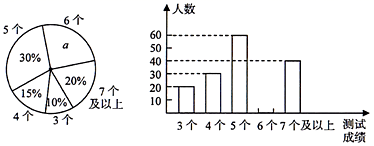 请你根据图中的信息,解答下列问题:(1)写出扇形图中
请你根据图中的信息,解答下列问题:(1)写出扇形图中![]() ______,并补全条形图;(2)样本数据的平均数是______,众数是______,中位数是______;(3)该区体育中考选报引体向上的男生共有1200人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名? 23.(12分)在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
______,并补全条形图;(2)样本数据的平均数是______,众数是______,中位数是______;(3)该区体育中考选报引体向上的男生共有1200人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名? 23.(12分)在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据: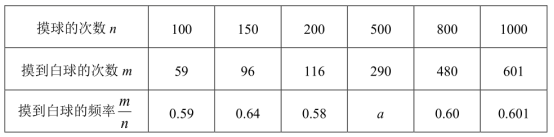 (1)上表中的a= ;(2)“摸到白球”的概率的估计值是 (精确到0.1)(3)试估算口袋中黑、白两种颜色的球各有多少个? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、B3、B4、B5、B6、D7、B8、C9、C10、B11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、3
(1)上表中的a= ;(2)“摸到白球”的概率的估计值是 (精确到0.1)(3)试估算口袋中黑、白两种颜色的球各有多少个? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、B3、B4、B5、B6、D7、B8、C9、C10、B11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、3![]() 14、①②③15、116、
14、①②③15、116、![]() 17、
17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(2)当点
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(2)当点![]() 位于
位于![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,见解析.19、(1)证明见解析;(2)45°;(3)105°,127.5°或 150°.20、解:(1)平均数是25人,众数是25人,中位数是26人;(2)1250 人.21、(1)①全等;②DE=BF+EF;(2)DE=BF-EF,见解析22、(1)25%,图形见解析;(2)5.3,5,5;(3)540名23、 (1) 0.58;(2) 0.6;(3)白球12(个),黑球8 (个)
是矩形,见解析.19、(1)证明见解析;(2)45°;(3)105°,127.5°或 150°.20、解:(1)平均数是25人,众数是25人,中位数是26人;(2)1250 人.21、(1)①全等;②DE=BF+EF;(2)DE=BF-EF,见解析22、(1)25%,图形见解析;(2)5.3,5,5;(3)540名23、 (1) 0.58;(2) 0.6;(3)白球12(个),黑球8 (个)
相关试卷
这是一份西藏拉萨北京实验中学2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了如图,点A在函数y=等内容,欢迎下载使用。
这是一份潮安龙湖中学2022-2023学年数学七下期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了若函数y=等内容,欢迎下载使用。
这是一份安徽宣城古泉中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了下列函数中,是一次函数的是,下列运算正确的是等内容,欢迎下载使用。








