


成都市教科院附属学校2022-2023学年数学七年级第二学期期末质量跟踪监视试题含答案
展开成都市教科院附属学校2022-2023学年数学七年级第二学期期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.若分式![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
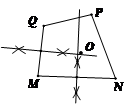
A.点M B.点N C.点P D.点Q
3.随机抽取10名八年级同学调查每天使用零花钱的情况,结果如表,则这10名同学每天使用零花钱的中位数是![]()
![]()
每天使用零花钱情况 单位(元 | 2 | 3 | 4 | 5 |
人数 | 1 | 5 | 2 | 2 |
A.2元 B.3元 C.4元 D.5元
4.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
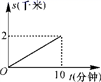
A.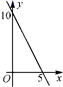 B.
B.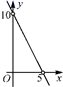 C.
C.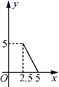 D
D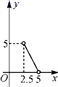
5.对于数据3,3,1,3,6,3,10,3,6,3,1.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中正确的结论有( )
A.1个 B.1个 C.3个 D.4个
6.能判定四边形是平行四边形的条件是( )
A.一组对边平行,另一组对边相等
B.一组对边相等,一组邻角相等
C.一组对边平行,一组邻角相等
D.一组对边平行,一组对角相等
7.已知直线 y=-x+6交x轴于点A,交y轴于点B,点P在线段OA上,将△PAB沿BP翻折,点A的对应点A′恰好落在y轴上,则![]() 的值为( )
的值为( )
A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
8.下列各组数中,以它们为边的三角形是直角三角形的是( )
A.1,2,3 B.9,16,25 C.12,15,20 D.1,2,![]()
9.下列方程中,判断中错误的是( )
A.方程![]() 是分式方程 B.方程
是分式方程 B.方程![]() 是二元二次方程
是二元二次方程
C.方程![]() 是无理方程 D.方程
是无理方程 D.方程![]() 是一元二次方程
是一元二次方程
10.一次环保知识竞赛共有25道题,每一题答对得4分,答错或不答都扣1分,在这次竟赛中,小明被评为优秀(85分或85分以上),小明至少要答对多少道题?如果设小明答对了x道题,根据题意列式得( )
A.4x﹣1×(25﹣x)>85 B.4x+1×(25﹣x)≤85
C.4x﹣1×(25﹣x)≥85 D.4x+1×(25﹣x)>85
二、填空题(本大题共有6小题,每小题3分,共18分)
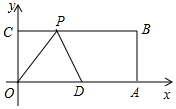
11.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为![]() ,
,![]() ,
,![]() ,点P在BC(不与点B、C重合)上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.
,点P在BC(不与点B、C重合)上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.
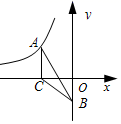
12.如图,点![]() 在双曲线
在双曲线![]() 上,
上,![]() 为
为![]() 轴上的一点,过点
轴上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积是3,则
的面积是3,则![]() __.
__.
13.如果多边形的每个外角都是45°,那么这个多边形的边数是_____.
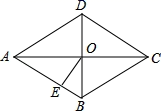
14.如图所示,在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() .OE⊥AB,垂足为
.OE⊥AB,垂足为![]() ,若
,若![]() ,则
,则![]() 的大小为____________.
的大小为____________.
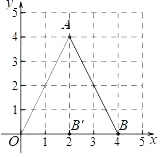
15.如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为_____.
16.《九章算术》中记载:今有户不知高、广,竿不知长、短,横之不出四尺,纵之不出二尺,邪之适出.问户高、广、邪各几何?这段话翻译后是:今有门,不知其高、宽,有竿,不知其长、短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为x尺,则可列方程为_____.
三、解下列各题(本大题共8小题,共72分)
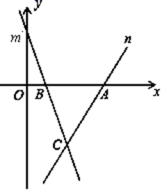
17.(8分)如图,直线m的表达式为y =﹣3x+3,且与x轴交于点B,直线n经过点A(4,0),且与直线m交于点C(t,﹣3)
(1)求直线n的表达式.
(2)求△ABC的面积.
(3)在直线n上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标是 .
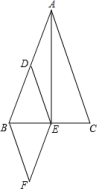
18.(8分)如图,在![]() 中,
中,![]() ,
,![]() 是中线,点
是中线,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,且
,且![]() ,
,![]()
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,直接写出四边形
,直接写出四边形![]() 的面积.
的面积.
19.(8分)光明玩具商店用800元购进若干套悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用1500元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元?
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于20%,那么每套悠悠球的售价至少是多少元?
20.(8分)如图,将![]() 的边
的边![]() 延长到点
延长到点![]() ,使
,使![]() ,交边
,交边![]() 于点
于点![]() .
.
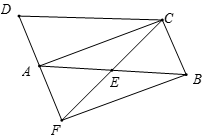
![]() 求证:
求证:![]()
![]() 若
若![]() ,求证:四边形
,求证:四边形![]() 是矩形
是矩形
21.(8分)如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB,PE与DC交于点O.
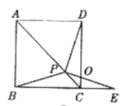
(基础探究)
(1)求证:PD=PE.
(2)求证:∠DPE=90°
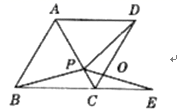
(3)(应用拓展)把正方形ABCD改为菱形,其他条件不变(如图),若PE=3,则PD=________;
若∠ABC=62°,则∠DPE=________.
22.(10分)某工厂从外地购得A种原料16吨,B种原料13吨,现计划租用甲、乙两种货车6辆将购得的原料一次性运回工厂,已知一辆甲种货车可装2吨A种原料和3吨B种原料;一辆乙种货车可装3吨A种原料和2吨B种原料,设安排甲种货车x辆.
(1)如何安排甲、乙两种货车?写出所有可行方案;
(2)若甲种货车的运费是每辆500元,乙种货车的运费是每辆350元,设总运费为W元,求W(元)与x(辆)之间的函数关系式;
(3)在(2)的前提下,当x为何值时,总运费最少,此时总运费是多少元?
23.(10分)为了从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶10次,命中的环数如下:
甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
如果你是教练你会选拔谁参加比赛?为什么?
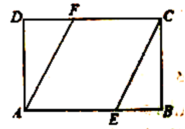
24.(12分)已知:如图,在矩形![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,
边上,![]() ,连接
,连接![]() ,
,![]() .求证:
.求证:![]() .
.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、B
4、D
5、A
6、D
7、C
8、D
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、(1,3)或(4,3)
12、-6
13、1
14、65°
15、(1,2)
16、x1=(x﹣4)1+(x﹣1)1
三、解下列各题(本大题共8小题,共72分)
17、(1)n的表达式为![]() ;(2)S△ABC的面积是4.5;(3)P点坐标为(6,3).
;(2)S△ABC的面积是4.5;(3)P点坐标为(6,3).
18、(1)见解析;(2)![]() .
.
19、(1)20;(2)27.1.
20、 ()证明见解析;(2)证明见解析.
21、(1)证明见解析;(2)证明见解析;(3)![]() ,
,![]() .
.
22、 (1)有两种可行方案,方案一:安排甲种货车1辆,乙种货车5辆,方案二:安排甲种货车2辆,乙种货车4辆;
(2) x为1时,总运费最少,此时总运费是2250元.
23、乙同学的成绩较稳定,应选乙参加比赛
24、见解析
2023-2024学年成都市高新区新城学校数学九上期末质量跟踪监视试题含答案: 这是一份2023-2024学年成都市高新区新城学校数学九上期末质量跟踪监视试题含答案,共7页。
2023-2024学年成都市教科院附属学校九上数学期末考试模拟试题含答案: 这是一份2023-2024学年成都市教科院附属学校九上数学期末考试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如图,在中,,则劣弧的度数为等内容,欢迎下载使用。
2023-2024学年山西农业大学附属学校九上数学期末质量跟踪监视试题含答案: 这是一份2023-2024学年山西农业大学附属学校九上数学期末质量跟踪监视试题含答案,共7页。试卷主要包含了下列事件是必然事件的是,的值为等内容,欢迎下载使用。












