


江苏南京市东山外国语学校2022-2023学年数学七下期末统考试题含答案
展开
这是一份江苏南京市东山外国语学校2022-2023学年数学七下期末统考试题含答案,共7页。试卷主要包含了抛物线的顶点坐标是,已知,则的值为等内容,欢迎下载使用。
江苏南京市东山外国语学校2022-2023学年数学七下期末统考试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列命题中,逆命题是真命题的是( )A.直角三角形的两锐角互余B.对顶角相等C.若两直线垂直,则两直线有交点D.若x=1,则x2=12.如图, ![]() 中,
中, ![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( ) 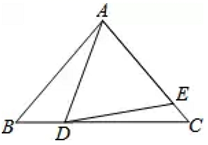 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.边长为3cm的菱形的周长是( )A.15cm B.12cm C.9cm D.3cm4.抛物线
3.边长为3cm的菱形的周长是( )A.15cm B.12cm C.9cm D.3cm4.抛物线![]() 的顶点坐标是( )A.
的顶点坐标是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.如图,在正方形 ABCD 中,BD=2,∠DCE 是正方形 ABCD 的外角,P 是∠DCE 的角平分线 CF 上任意一点,则△PBD 的面积等于 ( )
5.如图,在正方形 ABCD 中,BD=2,∠DCE 是正方形 ABCD 的外角,P 是∠DCE 的角平分线 CF 上任意一点,则△PBD 的面积等于 ( )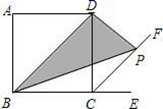 A.1 B.1.5 C.2 D.2.56.已知
A.1 B.1.5 C.2 D.2.56.已知![]() ,则
,则![]() 的值为( )A.
的值为( )A.![]() B.-2 C.
B.-2 C.![]() D.27.将五个边长都为 2
D.27.将五个边长都为 2![]() 的正方形按如图所示摆放,点
的正方形按如图所示摆放,点 ![]() 分别是四个正方形的中心,则图中四块阴影面积的和为( )
分别是四个正方形的中心,则图中四块阴影面积的和为( )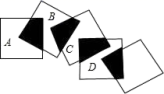 A.2
A.2![]() B.4
B.4![]() C.6
C.6![]() D.8
D.8![]() 8.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
8.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )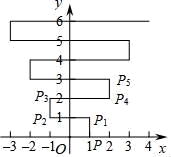 A.(﹣26,50) B.(﹣25,50)C.(26,50) D.(25,50)9.如图,在梯形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于E,∠BAE=∠EAC,O是AC的中点,AD=DC=2,下面结论:①AC=2AB;②AB=
A.(﹣26,50) B.(﹣25,50)C.(26,50) D.(25,50)9.如图,在梯形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于E,∠BAE=∠EAC,O是AC的中点,AD=DC=2,下面结论:①AC=2AB;②AB=![]() ;③S△ADC=2S△ABE;④BO⊥AE,其中正确的个数是( )
;③S△ADC=2S△ABE;④BO⊥AE,其中正确的个数是( )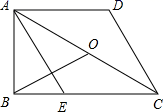 A.1 B.2 C.3 D.410.如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了( )米路,却紧伤了花草。
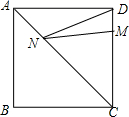
A.1 B.2 C.3 D.410.如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了( )米路,却紧伤了花草。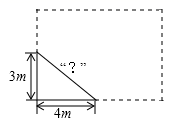 A.1 B.2 C.5 D.1211.如图,正方形ABCD的边长为8,点M在边DC上,且
A.1 B.2 C.5 D.1211.如图,正方形ABCD的边长为8,点M在边DC上,且![]() ,点N是边AC上一动点,则线段
,点N是边AC上一动点,则线段![]() 的最小值为
的最小值为![]()
![]()
 A.8B.
A.8B.![]() C.
C.![]() D.1012.如果小磊将镖随意投中如图所示的正方形木板(假设投中每个小正方形是等可能的),那么镖落在阴影部分的概率为( )
D.1012.如果小磊将镖随意投中如图所示的正方形木板(假设投中每个小正方形是等可能的),那么镖落在阴影部分的概率为( ) A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.一次函数y=2x-6的图像与x轴的交点坐标为 .14.在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D;(2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.老师说:“小明的作法正确.”请回答:小明这样折叠的依据是______________________________________.
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.一次函数y=2x-6的图像与x轴的交点坐标为 .14.在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D;(2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.老师说:“小明的作法正确.”请回答:小明这样折叠的依据是______________________________________.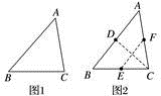 15.某种感冒病毒的直径是0.000 000 12米,用科学记数法表示为 米.16.已知m是一元二次方程
15.某种感冒病毒的直径是0.000 000 12米,用科学记数法表示为 米.16.已知m是一元二次方程![]() 的一个根 , 则代数式
的一个根 , 则代数式![]() 的值是_____17.如图,在平行四边形ABCD中,
的值是_____17.如图,在平行四边形ABCD中,![]() ,
,![]() ,垂足分别为E、F,
,垂足分别为E、F,![]() ,
,![]() ,
,![]() ,则平行四边形ABCD的面积为_________.
,则平行四边形ABCD的面积为_________.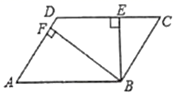 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,▱ABCD中,AC为对角线,G为CD的中点,连接AG并廷长交BC的延长线于点F,连接DF,求证:四边形ACFD为平行四边形.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,▱ABCD中,AC为对角线,G为CD的中点,连接AG并廷长交BC的延长线于点F,连接DF,求证:四边形ACFD为平行四边形.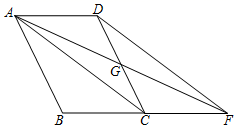 19.(5分)如图,平面直角坐标系中,直线AB:
19.(5分)如图,平面直角坐标系中,直线AB:![]() 交y轴于点
交y轴于点![]() ,交x轴于点B.
,交x轴于点B.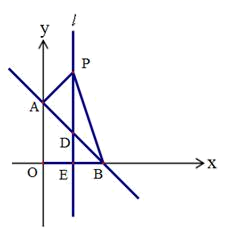 (1)求直线AB的表达式和点B的坐标; (2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.①当
(1)求直线AB的表达式和点B的坐标; (2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.①当![]() 时,求点P的坐标;②在①的条件下,以PB为斜边在第一象限作等腰直角
时,求点P的坐标;②在①的条件下,以PB为斜边在第一象限作等腰直角![]() ,求点C的坐标. 20.(8分)(1)计算:5
,求点C的坐标. 20.(8分)(1)计算:5![]() -
-![]() +2
+2![]() (2)解不等式组:
(2)解不等式组: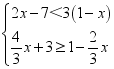 21.(10分)解不等式组
21.(10分)解不等式组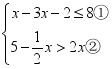 并求其整数解的和.解:解不等式①,得_______;解不等式②,得________;把不等式①和②的解集在数轴上表示出来:
并求其整数解的和.解:解不等式①,得_______;解不等式②,得________;把不等式①和②的解集在数轴上表示出来:![]()
![]() 原不等式组的解集为________,由数轴知其整数解为________,和为________.在解答此题的过程中我们借助于数轴上,很直观地找出了原不等式组的解集及其整数解,这就是“数形结合的思想”,同学们要善于用数形结合的思想去解决问题. 22.(10分)如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
原不等式组的解集为________,由数轴知其整数解为________,和为________.在解答此题的过程中我们借助于数轴上,很直观地找出了原不等式组的解集及其整数解,这就是“数形结合的思想”,同学们要善于用数形结合的思想去解决问题. 22.(10分)如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.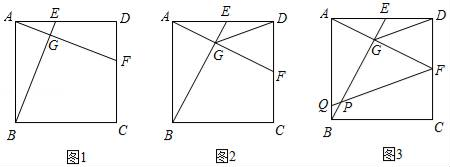 (1)写出BE与AF之间的关系,并证明你的结论;(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长;(3)如图3,在(2)的条件下,作FQ∥DG交AB于点Q,请直接写出FQ的长. 23.(12分)2018年8月中国铁路总公司宣布,京津高铁将再次提速,担任此次运营任务是最新的复兴号动车组,提速后车速是之前的1.5倍,100千米缩短了10分钟,问提速前后的速度分别是多少千米每小时? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、B3、B4、D5、A6、C7、B8、C9、D10、B11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、(3,0).14、对角线互相垂直平分的四边形是菱形15、
(1)写出BE与AF之间的关系,并证明你的结论;(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长;(3)如图3,在(2)的条件下,作FQ∥DG交AB于点Q,请直接写出FQ的长. 23.(12分)2018年8月中国铁路总公司宣布,京津高铁将再次提速,担任此次运营任务是最新的复兴号动车组,提速后车速是之前的1.5倍,100千米缩短了10分钟,问提速前后的速度分别是多少千米每小时? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、B3、B4、D5、A6、C7、B8、C9、D10、B11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、(3,0).14、对角线互相垂直平分的四边形是菱形15、![]() 16、
16、![]() .17、
.17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、见解析19、(1)(1,0);(2)①(2,3);②(3,1)20、(1)5
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、见解析19、(1)(1,0);(2)①(2,3);②(3,1)20、(1)5![]() ;(2)-1≤x<1.21、详见解析.22、(1)BE=AF,BE⊥AF;(2)GD是∠EGF的角平分线,证明见解析,GD=
;(2)-1≤x<1.21、详见解析.22、(1)BE=AF,BE⊥AF;(2)GD是∠EGF的角平分线,证明见解析,GD=![]() ;(3)FQ=
;(3)FQ=![]() .23、提速前的速度为200千米/小时,提速后的速度为350千米/小时,
.23、提速前的速度为200千米/小时,提速后的速度为350千米/小时,
相关试卷
这是一份江苏南京市东山外国语学校2023-2024学年九上数学期末统考试题含答案,共7页。试卷主要包含了方程x=x的根是等内容,欢迎下载使用。
这是一份2023-2024学年江苏省南京市东山外国语学校九上数学期末经典模拟试题含答案,共9页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份2023-2024学年江苏南京市东山外国语学校数学八上期末学业质量监测试题含答案,共8页。试卷主要包含了估算的值在,已知,下列命题中,是假命题的是,点A等内容,欢迎下载使用。









