昆明市学校际合作学校2022-2023学年七下数学期末检测试题含答案

这是一份昆明市学校际合作学校2022-2023学年七下数学期末检测试题含答案，共7页。试卷主要包含了考生要认真填写考场号和座位序号，若，则的值用、可以表示为等内容，欢迎下载使用。
昆明市学校际合作学校2022-2023学年七下数学期末检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考生要认真填写考场号和座位序号。2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。 一、选择题(每小题3分,共30分)1．若分式有意义，则实数的取值范围是（    ）A． B． C． D．2．一组数据3,4,4,5,5,5,6,6,7众数是（   ）A．4 B．5 C．6 D．73．已知、、是的三边，且满足，则的形状是（    ）A．等腰三角形 B．等边三角形C．直角三角形 D．不能确定4．若，则的值用、可以表示为                     （　 　）A． B． C． D．5．下列图形既是轴对称图形，又是中心对称图形的是（    ）A． B． C． D．6．一个多边形的每一个外角都等于它相邻的内角的一半，则这个多边形的边数是（    ）A．3 B．4 C．5 D．67．若一个多边形的内角和为外角和的3倍，则这个多边形为 （　　）A．八边形 B．九边形 C．十边形 D．十二边形8．为参加学校举办的“诗意校园•致远方”朗诵艺术大赛，八年级“屈原读书社”组织了五次选拔赛，这五次选拔赛中，小明五次成绩的平均数是90，方差是2；小强五次成绩的平均数也是90，方差是14.1．下列说法正确的是（　　）A．小明的成绩比小强稳定B．小明、小强两人成绩一样稳定C．小强的成绩比小明稳定D．无法确定小明、小强的成绩谁更稳定9．如图，将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD，连接CD．若AB=4cm．则△BCD的面积为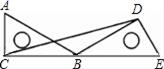（　　）A．4 B．2 C．3 D．210．要使矩形ABCD为正方形，需要添加的条件是（　　）A．AB=BC B．AD=BC C．AB=CD D．AC=BD二、填空题(本大题共有6小题，每小题3分，共18分)11．数学兴趣小组的甲、乙、丙、丁四位同学进行还原魔方练习，下表记录了他们次还原魔方所用时间的平均值与方差： 甲乙丙丁（秒）要从中选择一名还原魔方用时少又发挥稳定的同学参加比赛，应该选择________同学．12．最简二次根式与是同类二次根式，则＝________．13．在关系式V=31-2t中，V随着t的变化而变化，其中自变量是_____，因变量是_____，当t=_____时，V=1．14．计算：=___________15．某老师为了解学生周末学习时间的情况，在所任班级中随机调查了10名学生，绘成如图所示的条形统计图，则这10名学生周末学习的平均时间是_______小时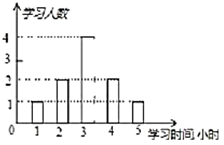．16．已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的用电器，其限制电流不能超过10A，那么用电器可变电阻R应控制的范围是____.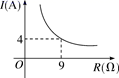三、解下列各题(本大题共8小题，共72分)17．（8分）我市某游乐场在暑假期间推出学生个人门票优惠活动，各类门票价格如下表：某慈善单位欲购买三种类型的门票共张奖励品学兼优的留守学生，设购买种票张，种票张数是种票的倍还多张，种票张，根据以上信息解答下列问题：（1）写出y与x之间的函数关系式；（2）设购票总费用为元，求（元）与（张）之间的函数关系式；（3）为方便学生游玩，计划购买学生的夜场票不低于张，且节假日通用票至少购买张，有哪几种购票方案？哪种方案费用最少？   18．（8分）如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=BC，连接CD和EF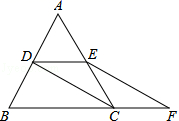．（1）求证：DE=CF；（2）求EF的长．   19．（8分）如图，在矩形ABCD中，AB=3cm，BC=6cm．点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．（1）当t为何值时，四边形ABQP是矩形；（2）当t为何值时，四边形AQCP是菱形；（3）分别求出（2）中菱形AQCP的周长和面积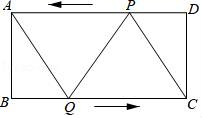．   20．（8分）已知△ABC中， ∠ACB=90°，∠CAB=30°，以AC，AB为边向外作等边三角形ACD和等边三角形ABE，点F在AB上，且到AE，BE的距离相等．（1）用尺规作出点F； (要求：尺规作图，保留作图痕迹，不写作法)（2）连接EF，DF，证明四边形ADFE为平行四边形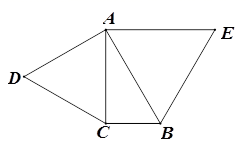．   21．（8分）如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：（1）在图①中画一条线段AB，使AB＝ ；（2）在图②中画一个以格点为顶点，面积为2的正方形ABCD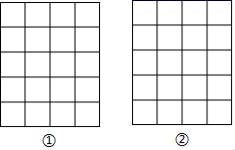．   22．（10分）如图，正方形ABCD，点P为射线DC上的一个动点，点Q为AB的中点，连接PQ，DQ，过点P作PE⊥DQ于点E．（1）请找出图中一对相似三角形，并证明；（2）若AB＝4，以点P，E，Q为顶点的三角形与△ADQ相似，试求出DP的长．   23．（10分）如图，已知四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．(1)求证：矩形DEFG是正方形．(2)当点E从A点运动到C点时；①求证：∠DCG的大小始终不变；②若正方形ABCD的边长为2，则点G运动的路径长为 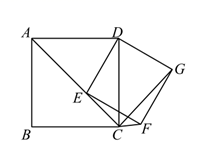        ．   24．（12分）（1）如图（1），已知：正方形ABCD的对角线交于点O，E是AC上的一动点，过点A作AG⊥BE于G，交BD于F．求证：OE＝OF．（2）在（1）的条件下，若E点在AC的延长线上，以上结论是否成立，为什么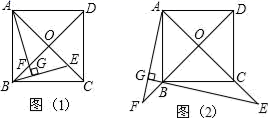？   参考答案 一、选择题(每小题3分,共30分)1、B2、B3、B4、C5、D6、D7、C8、A9、C10、A 二、填空题(本大题共有6小题，每小题3分，共18分)11、丁12、2113、t    V    15    14、615、316、R≥3.1 三、解下列各题(本大题共8小题，共72分)17、（1）；（2）；（3）共有种购票方案：；；；当种票为张，种票张，种票为张时费用最少，最少费用元.18、见解析；19、（1）t=3，ABQP是矩形；（2）t=，AQCP是菱形；（3）周长为:15cm，面积为：（cm2）.20、（1）详见解析；（2）详见解析21、（1）详见解析；（2）详见解析．22、（1）△DPE∽△QDA，证明见解析；（2）DP=2或523、 (1)详见解析;（2）①详见解析;②24、（1）详见解析；（2）以上结论仍然成立．