


昆明市重点中学2022-2023学年七下数学期末教学质量检测模拟试题含答案
展开
这是一份昆明市重点中学2022-2023学年七下数学期末教学质量检测模拟试题含答案,共7页。试卷主要包含了下列各式等内容,欢迎下载使用。
昆明市重点中学2022-2023学年七下数学期末教学质量检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.如图,A、B、C、D四点都在⊙O上,若OCAB,AOC70,则圆周角D的度数等于( )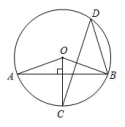 A.70 B.50 C.35 D.202.一元一次不等式组
A.70 B.50 C.35 D.202.一元一次不等式组![]() 的解集为x>a,且a≠b,则a与b的关系是( )A.a>b B.a<b C.a>b>0 D.a<b<03.如图所示,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
的解集为x>a,且a≠b,则a与b的关系是( )A.a>b B.a<b C.a>b>0 D.a<b<03.如图所示,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )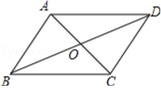 A.△AOB的面积等于△AOD的面积 B.当AC⊥BD时,它是菱形C.当OA=OB时,它是矩形 D.△AOB的周长等于△AOD的周长4.如图1,在矩形
A.△AOB的面积等于△AOD的面积 B.当AC⊥BD时,它是菱形C.当OA=OB时,它是矩形 D.△AOB的周长等于△AOD的周长4.如图1,在矩形![]() 中,动点
中,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动至点
方向运动至点![]() 处停止.设点
处停止.设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,如果
,如果![]() 关于
关于![]() 的函致图象如图2所示,则矩形
的函致图象如图2所示,则矩形![]() 的周长是( )
的周长是( )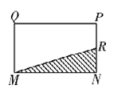
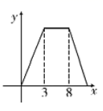 图1 图2A.
图1 图2A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.4名选手在相同条件下各射靶10次,统计结果如下表,表现较好且更稳定的是( )选手甲乙丙丁平均环数99.599.5方差4.5445.4A.甲 B.乙 C.丙 D.丁6.下列各式:①
5.4名选手在相同条件下各射靶10次,统计结果如下表,表现较好且更稳定的是( )选手甲乙丙丁平均环数99.599.5方差4.5445.4A.甲 B.乙 C.丙 D.丁6.下列各式:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,最简二次根式有( )A.1个 B.2个 C.3个 D.4个7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )A.2 B.3 C.4 D.58.已知不等式ax+b>0的解集是x<-2,则函数y=ax+b的图象可能是( )A.
中,最简二次根式有( )A.1个 B.2个 C.3个 D.4个7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )A.2 B.3 C.4 D.58.已知不等式ax+b>0的解集是x<-2,则函数y=ax+b的图象可能是( )A.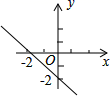 B.
B.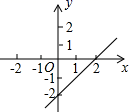 C.
C.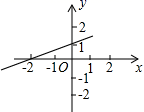 D.
D.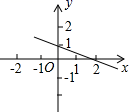 9.已知n是自然数,
9.已知n是自然数,![]() 是整数,则n最小为( )A.0 B.2 C.4 D.4010.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体C.1000名九年级学生是总体的一个样本 D.样本容量是1000二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,平行四边形AOBC中,对角线交于点E,双曲线
是整数,则n最小为( )A.0 B.2 C.4 D.4010.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体C.1000名九年级学生是总体的一个样本 D.样本容量是1000二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,平行四边形AOBC中,对角线交于点E,双曲线![]() (k>0)经过A,E两点,若平行四边形AOBC的面积为24,则k=____.
(k>0)经过A,E两点,若平行四边形AOBC的面积为24,则k=____.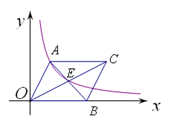 12.如图,在
12.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点P是边AB上的一个动点,以每秒3个单位的速度按照从
,若点P是边AB上的一个动点,以每秒3个单位的速度按照从![]() 运动,同时点Q从
运动,同时点Q从![]() 以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若
以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若![]() 为直角三角形,则t的值为________.
为直角三角形,则t的值为________.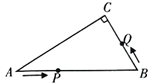 13.将
13.将![]() 代入反比例函数
代入反比例函数![]() 中,所得函数值记为
中,所得函数值记为![]() ,又将
,又将![]() 代入函数中,所得函数值记为
代入函数中,所得函数值记为![]() ,再将
,再将![]() 代入函数中,所得函数值记为
代入函数中,所得函数值记为![]()
![]() ,如此继续下去,则
,如此继续下去,则![]() ________.14.已知关于x的分式方程
________.14.已知关于x的分式方程![]() 有一个正数解,则k的取值范围为________.15.函数
有一个正数解,则k的取值范围为________.15.函数![]() 的自变量的取值范围是
的自变量的取值范围是![]() .16.关于x的方程
.16.关于x的方程![]() =3有增根,则m的值为___________.三、解下列各题(本大题共8小题,共72分)17.(8分)为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.甲、乙射击成绩统计表平均数(环)中位数(环)方差命中10环的次数甲7 0乙 1甲、乙射击成绩折线统计图
=3有增根,则m的值为___________.三、解下列各题(本大题共8小题,共72分)17.(8分)为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.甲、乙射击成绩统计表平均数(环)中位数(环)方差命中10环的次数甲7 0乙 1甲、乙射击成绩折线统计图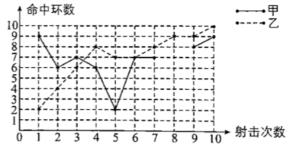 (1)请补全上述图表(请直接在表中填空和补全折线图);(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么? 18.(8分)如图平行四边形ABCD中,对角线AC与BD相交于O,E.F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形
(1)请补全上述图表(请直接在表中填空和补全折线图);(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么? 18.(8分)如图平行四边形ABCD中,对角线AC与BD相交于O,E.F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形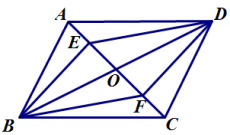 19.(8分)已知:如图,直线y=﹣x+6与坐标轴分别交于A、B两点,点C是线段AB上的一个动点,连接OC,以OC为边在它的左侧作正方形OCDE连接BE、CE.(1)当点C横坐标为4时,求点E的坐标;(2)若点C横坐标为t,△BCE的面积为S,请求出S关于t的函数解析式;(3)当点C在线段AB上运动时,点E相应随之运动,请求出点E所在的函数解析式.
19.(8分)已知:如图,直线y=﹣x+6与坐标轴分别交于A、B两点,点C是线段AB上的一个动点,连接OC,以OC为边在它的左侧作正方形OCDE连接BE、CE.(1)当点C横坐标为4时,求点E的坐标;(2)若点C横坐标为t,△BCE的面积为S,请求出S关于t的函数解析式;(3)当点C在线段AB上运动时,点E相应随之运动,请求出点E所在的函数解析式.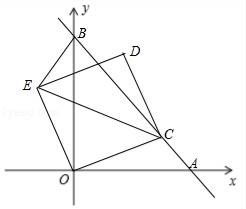 20.(8分)某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)求y与x之间的函数表达式;(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润. 21.(8分)如图,BD是▱ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.
20.(8分)某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)求y与x之间的函数表达式;(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润. 21.(8分)如图,BD是▱ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.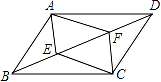 22.(10分)已知四边形ABCD是矩形,对角线AC和BD相交于点F,
22.(10分)已知四边形ABCD是矩形,对角线AC和BD相交于点F,![]() ,
,![]() .
.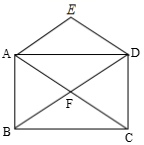 (1)求证:四边形DEAF是菱形;(2)若
(1)求证:四边形DEAF是菱形;(2)若![]() ,求
,求![]() 的度数. 23.(10分)如图,在平面直角坐标系中,点
的度数. 23.(10分)如图,在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() ,连接
,连接![]() (1)菱形
(1)菱形![]() 的边长是________;(2)求直线
的边长是________;(2)求直线![]() 的解析式;(3)动点
的解析式;(3)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以2个单位长度/秒的速度向终点
以2个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.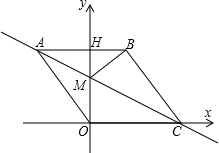 24.(12分)某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:应试者面试笔试甲8690乙9283(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取? 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、D4、C5、B6、A7、B8、A9、C10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、
24.(12分)某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:应试者面试笔试甲8690乙9283(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取? 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、D4、C5、B6、A7、B8、A9、C10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、![]() 或
或![]() 或
或![]() 13、214、k<6且k≠1 15、x≠116、m=-1. 三、解下列各题(本大题共8小题,共72分)17、(1)补图见解析;(2)甲胜出,理由见解析;(3)见解析.18、见解析19、(1)(﹣2,4);(2)S=﹣t2+1t;(3)y=x+120、(1)
13、214、k<6且k≠1 15、x≠116、m=-1. 三、解下列各题(本大题共8小题,共72分)17、(1)补图见解析;(2)甲胜出,理由见解析;(3)见解析.18、见解析19、(1)(﹣2,4);(2)S=﹣t2+1t;(3)y=x+120、(1)![]() ;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.21、见解析22、 (1)证明见解析;(2)
;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.21、见解析22、 (1)证明见解析;(2)![]() .23、(1)5;(2)y=-
.23、(1)5;(2)y=-![]() ;(3)S=
;(3)S=![]() t-
t-![]() .24、 (1)甲将被录取;(2)乙将被录取.
.24、 (1)甲将被录取;(2)乙将被录取.
相关试卷
这是一份鸡西市重点中学2022-2023学年数学七下期末教学质量检测模拟试题含答案,共7页。试卷主要包含了下列计算正确的是,有下列的判断,整数满足,则的值为等内容,欢迎下载使用。
这是一份辽源市重点中学2022-2023学年七下数学期末教学质量检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
这是一份丽水市重点中学2022-2023学年七下数学期末教学质量检测模拟试题含答案,共6页。试卷主要包含了﹣2的绝对值是等内容,欢迎下载使用。








