


武汉六中学2022-2023学年数学七下期末复习检测试题含答案
展开
这是一份武汉六中学2022-2023学年数学七下期末复习检测试题含答案,共7页。
武汉六中学2022-2023学年数学七下期末复习检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题(每小题3分,共30分)1.根据以下程序,当输入x=﹣2时,输出结果为( ) A.﹣5 B.﹣2 C.0 D.32.下列式子从左到右的变形中,属于因式分解的是( )A.10
A.﹣5 B.﹣2 C.0 D.32.下列式子从左到右的变形中,属于因式分解的是( )A.10![]() 2-5
2-5![]() =5
=5![]() (2
(2![]() -1) B.
-1) B.![]() (
(![]() +y) =
+y) =![]()
![]() +
+![]() C.
C.![]() 2-4
2-4![]() +4=
+4=![]() (
(![]() -4)+4 D.
-4)+4 D.![]() 2-16+3
2-16+3![]() =(
=(![]() -4)(
-4)(![]() +4)+3
+4)+3![]() 3.如图,将边长为
3.如图,将边长为![]() 的正方形绕点B逆时针旋转30°,那么图中点M的坐标为( )
的正方形绕点B逆时针旋转30°,那么图中点M的坐标为( )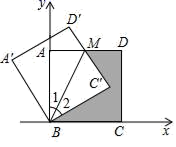 A.(
A.(![]() ,1) B.(1,
,1) B.(1,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )4.如图,正方形
)4.如图,正方形![]() 中,
中,![]() ,连接
,连接![]() 交对角线
交对角线![]() 于点
于点![]() ,那么
,那么![]() ( )
( )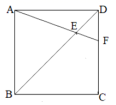 A.
A.![]() B.
B.![]() C.
C.![]() D.
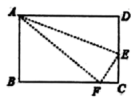
D.![]() 5.如图,在长方形
5.如图,在长方形![]() 中,
中,![]() ,在
,在![]() 上存在一点
上存在一点![]() ,沿直线
,沿直线![]() 把
把![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,若
处,若![]() 的面积为
的面积为![]() ,那么折叠的
,那么折叠的![]() 的面积为( )
的面积为( )![]()
 A.30 B.20 C.
A.30 B.20 C.![]() D.
D.![]() 6.如图,△DEF是由△ABC经过平移得到的,若∠C=80°,∠A=33°,则∠EDF=( )
6.如图,△DEF是由△ABC经过平移得到的,若∠C=80°,∠A=33°,则∠EDF=( )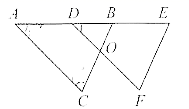 A.33° B.80° C.57° D.67°7.利用反证法证明命题“四边形中至少有一个角是钝角或直角”时,应假设( )A.四边形中至多有一个内角是钝角或直角B.四边形中所有内角都是锐角C.四边形的每一个内角都是钝角或直角D.四边形中所有内角都是直角8.若顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是( )A.平行四边形 B.矩形C.对角线相等的四边形 D.对角线互相垂直的四边形9.如图,在▱ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
A.33° B.80° C.57° D.67°7.利用反证法证明命题“四边形中至少有一个角是钝角或直角”时,应假设( )A.四边形中至多有一个内角是钝角或直角B.四边形中所有内角都是锐角C.四边形的每一个内角都是钝角或直角D.四边形中所有内角都是直角8.若顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是( )A.平行四边形 B.矩形C.对角线相等的四边形 D.对角线互相垂直的四边形9.如图,在▱ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )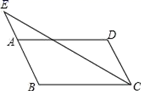 A.3 B.2.5 C.2 D.1.510.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( )A.20 B.30 C.0.4 D.0.6二、填空题(本大题共有6小题,每小题3分,共18分)11.方程x3=8的根是______.12.若分式
A.3 B.2.5 C.2 D.1.510.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( )A.20 B.30 C.0.4 D.0.6二、填空题(本大题共有6小题,每小题3分,共18分)11.方程x3=8的根是______.12.若分式![]() 的值为零,则x=___________。13.因式分解:
的值为零,则x=___________。13.因式分解:![]() .14.不等式
.14.不等式![]() 的正整数解有______个
的正整数解有______个![]() 15.在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D;(2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.老师说:“小明的作法正确.”请回答:小明这样折叠的依据是______________________________________.
15.在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D;(2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.老师说:“小明的作法正确.”请回答:小明这样折叠的依据是______________________________________.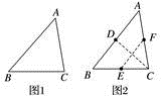 16.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是_____.
16.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是_____.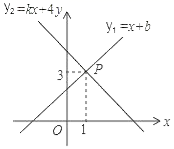 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.(1) 求证:△MEF是等腰三角形;(2) 若∠A=
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.(1) 求证:△MEF是等腰三角形;(2) 若∠A=![]() ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.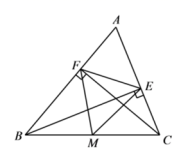 18.(8分)如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.
18.(8分)如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD. 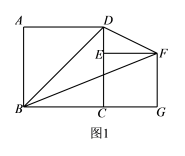
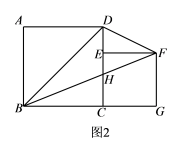 (1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想; (3)如图2,设BF与CD相交于点H,若△DFH的面积为
(1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想; (3)如图2,设BF与CD相交于点H,若△DFH的面积为![]() ,求正方形CEFG的边长. 19.(8分)甲、乙两车间同时开始加工—批服装.从开始加工到加工完这批服装甲车间工作了
,求正方形CEFG的边长. 19.(8分)甲、乙两车间同时开始加工—批服装.从开始加工到加工完这批服装甲车间工作了![]() 小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为
小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为![]() (件).甲车间加工的时间为
(件).甲车间加工的时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.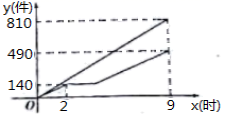 (1)甲车间每小时加工服装件数为 件;这批服装的总件数为 件;(2)求乙车间维修设备后,乙车间加工服装数量
(1)甲车间每小时加工服装件数为 件;这批服装的总件数为 件;(2)求乙车间维修设备后,乙车间加工服装数量![]() 与
与![]() 之间的函数关系式;(3)求甲、乙两车间共同加工完1140件服装时甲车间所用的时间. 20.(8分)(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
之间的函数关系式;(3)求甲、乙两车间共同加工完1140件服装时甲车间所用的时间. 20.(8分)(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.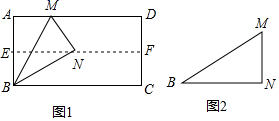 21.(8分)解方程: (1)2x2﹣x﹣6=0; (2)
21.(8分)解方程: (1)2x2﹣x﹣6=0; (2)![]() . 22.(10分)在甲、乙两个不透明的口袋中装有质地、大小相同的小球,甲袋中有2个白球,1个黄球和1个红球:乙袋中装有1个白球,1个黄球和若干个红球,从乙盒中仼意摸取一球为红球的概率是从甲盒中仼意摸取一球为红球的概率的2倍.(1)乙袋中红球的个数为 .(2)若摸到白球记1分,摸到黄球记2分,摸到红球记0分,小明从甲、乙两袋中先后分别任意摸取一球,请用树状图或列表的方法求小明摸得两个球得2分的概率. 23.(10分)如图,在
. 22.(10分)在甲、乙两个不透明的口袋中装有质地、大小相同的小球,甲袋中有2个白球,1个黄球和1个红球:乙袋中装有1个白球,1个黄球和若干个红球,从乙盒中仼意摸取一球为红球的概率是从甲盒中仼意摸取一球为红球的概率的2倍.(1)乙袋中红球的个数为 .(2)若摸到白球记1分,摸到黄球记2分,摸到红球记0分,小明从甲、乙两袋中先后分别任意摸取一球,请用树状图或列表的方法求小明摸得两个球得2分的概率. 23.(10分)如图,在![]() 中,过点
中,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.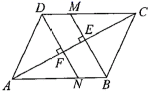 (1)求证:四边形
(1)求证:四边形![]() 是平行四边形;(2)已知
是平行四边形;(2)已知![]() ,求
,求![]() 的长. 24.(12分)
的长. 24.(12分)![]() 城有肥料
城有肥料![]() 吨,
吨,![]() 城有肥料
城有肥料![]() 吨,现要把这些肥料全部运往
吨,现要把这些肥料全部运往![]() 、
、![]() 两乡.从
两乡.从![]() 城运往
城运往![]() 、
、![]() 两乡运肥料的费用分别是每吨
两乡运肥料的费用分别是每吨![]() 元和
元和![]() 元,从
元,从![]() 城往
城往![]() 、
、![]() 两乡运肥料的费用分别为每吨
两乡运肥料的费用分别为每吨![]() 元和
元和![]() 元,现在
元,现在![]() 乡需要肥料
乡需要肥料![]() 吨,
吨,![]() 乡需要肥料
乡需要肥料![]() 吨,设
吨,设![]() 城运往
城运往![]() 乡的肥料量为
乡的肥料量为![]() 吨,总运费为
吨,总运费为![]() 元.(1)写出总运费
元.(1)写出总运费![]() 元与
元与![]() 之间的关系式;(2)当总费用为
之间的关系式;(2)当总费用为![]() 元,求从
元,求从![]() 、
、![]() 城分别调运
城分别调运![]() 、
、![]() 两乡各多少吨?(3)怎样调运化肥,可使总运费最少?最少运费是多少? 参考答案 一、选择题(每小题3分,共30分)1、B2、A3、B4、D5、D6、A7、B8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、212、113、
两乡各多少吨?(3)怎样调运化肥,可使总运费最少?最少运费是多少? 参考答案 一、选择题(每小题3分,共30分)1、B2、A3、B4、D5、D6、A7、B8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、212、113、![]() 14、315、对角线互相垂直平分的四边形是菱形16、x>1. 三、解下列各题(本大题共8小题,共72分)17、(1)见解析;(2)∠EMF=40°18、(1)1,1;(2)S△BDF=
14、315、对角线互相垂直平分的四边形是菱形16、x>1. 三、解下列各题(本大题共8小题,共72分)17、(1)见解析;(2)∠EMF=40°18、(1)1,1;(2)S△BDF=![]() S正方形ABCD,证明见解析;(3)219、(1)90,1300;(2)
S正方形ABCD,证明见解析;(3)219、(1)90,1300;(2)![]() ;(3)1.20、(1)30º,见解析.(2)
;(3)1.20、(1)30º,见解析.(2)![]() 21、 (1)
21、 (1) ![]() ,
,![]() ;(2)
;(2) ![]() .22、(1)2;(2)小明摸得两个球得2分的概率为
.22、(1)2;(2)小明摸得两个球得2分的概率为![]() .23、(1)见解析;(2)1324、(1)
.23、(1)见解析;(2)1324、(1)![]() ;(2)
;(2)![]() 城运往
城运往![]() 乡的肥料量为
乡的肥料量为![]() 吨,
吨,![]() 城运往
城运往![]() 乡的肥料量为
乡的肥料量为![]() 吨,
吨,![]() 城运往
城运往![]() 的肥料量分别为
的肥料量分别为![]() 吨,
吨,![]() 城运往
城运往![]() 的肥料量分别为
的肥料量分别为![]() 吨;(3)从
吨;(3)从![]() 城运往
城运往![]() 乡
乡![]() 吨,运往
吨,运往![]() 乡
乡![]() 吨;从
吨;从![]() 城运往
城运往![]() 乡
乡![]() 吨,运往
吨,运往![]() 乡
乡![]() 吨,此时总运费最少,总运费最小值是
吨,此时总运费最少,总运费最小值是![]() 元
元
相关试卷
这是一份湖北省武汉东湖高新区六校联考2022-2023学年七下数学期末复习检测试题含答案,共7页。
这是一份武汉新洲区六校联考2022-2023学年七下数学期末复习检测模拟试题含答案,共6页。试卷主要包含了已知 ,则的值为,已知P1,已知一次函数y=等内容,欢迎下载使用。
这是一份2022-2023学年甘肃省永昌六中学数学七下期末复习检测试题含答案,共8页。








