


江苏省东台市第六教育联盟2022-2023学年七下数学期末质量检测试题含答案
展开这是一份江苏省东台市第六教育联盟2022-2023学年七下数学期末质量检测试题含答案,共7页。试卷主要包含了如图直线l1,下列计算中,正确的是等内容,欢迎下载使用。
江苏省东台市第六教育联盟2022-2023学年七下数学期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() 且
且![]() D.
D.![]() 且
且![]()
2.点P(2,﹣3)关于y轴的对称点的坐标是( )
A.(2,3) B.(﹣2,﹣3) C.(﹣2,3) D.(﹣3,2)
3.如图,△ABC中AB=AC,点D在AC边上,且BD=BC=AD,则∠A度数为( )
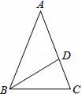
A.30° B.36° C.45° D.70°
4.若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程可能是( )
A.x2-3x+2=0 B.x2+3x+2=0 C.x2+3x-2=0 D.x2-2x+3=0
5.若![]() 有意义,则m能取的最小整数值是( )
有意义,则m能取的最小整数值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A.![]() =15 B.
=15 B.![]()
C.![]() D.
D.![]()
7.如图直线l1:y=ax+b,与直线l2:y=mx+n交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
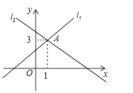
A.x>3 ![]() B.x<3
B.x<3 ![]() C.x>1
C.x>1 ![]() D.x<1
D.x<1
8.将长度为3cm的线段向上平移10cm,再向右平移8cm,所得线段的长是![]()
![]()
A.3cm B.8cm C.10cm D.无法确定
9.平南县某小区5月份随机抽取了15户家庭,对其用电情况进行了统计,统计情况如下(单位:度):78,62,95,108,87,103,99,74,87,105,88,76,76,94,79.则用电量在71~80的家庭有( )
A.4户 B.5户 C.6户 D.7户
10.下列计算中,正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知关于x的方程x2+(3﹣2k)x+k2+1=0的两个实数根分别是x1、x2,当|x1|+|x2|=7时,那么k的值是__.
12.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是______.
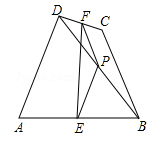
13.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .
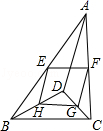
14.小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.
15.若直角三角形的两直角边长为a、b,且满足![]() ,则该直角三角形的斜边长为 .
,则该直角三角形的斜边长为 .
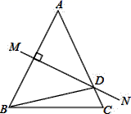
16.如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交边AC于点D,且∠DBC=15°,则∠A的度数是_______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在网格图中,平移![]() 使点
使点![]() 平移到点
平移到点![]() ,每小格代表1个单位。
,每小格代表1个单位。
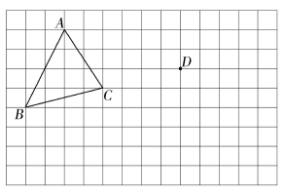
(1)画出平移后的![]() ;
;
(2)求![]() 的面积.
的面积.
18.(8分)在“母亲节”前夕,店主用不多于900元的资金购进康乃馨和玫瑰两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
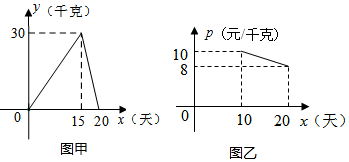
19.(8分)安德利水果超市购进一批时令水果,20天销售完毕,超市将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量![]() (千克)与销售时间
(千克)与销售时间![]() (天)之间的函数关系如图甲所示,销售单价
(天)之间的函数关系如图甲所示,销售单价![]() (元/千克)与销售时间
(元/千克)与销售时间![]() (天)之间的函数关系如图乙所示。
(天)之间的函数关系如图乙所示。
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)分别求出第10天和第15天的销售金额。
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
20.(8分)先化简再求值:![]() ,其中
,其中![]() .
.
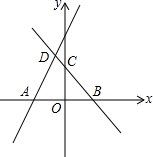
21.(8分)如图,直线![]() 与x轴交于点
与x轴交于点![]() ,直线
,直线![]() 与x轴、y轴分别交于B、C两点,并与直线
与x轴、y轴分别交于B、C两点,并与直线![]() 相交于点D,若
相交于点D,若![]() .
.
![]() 求点D的坐标;
求点D的坐标;
![]() 求出四边形AOCD的面积;
求出四边形AOCD的面积;
![]() 若E为x轴上一点,且
若E为x轴上一点,且![]() 为等腰三角形,写出点E的坐标
为等腰三角形,写出点E的坐标![]() 直接写出答案
直接写出答案![]() .
.
22.(10分)解不等式组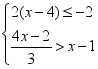 ,把解集在所给数轴上表示出来,并写出其整数解.
,把解集在所给数轴上表示出来,并写出其整数解.
![]()
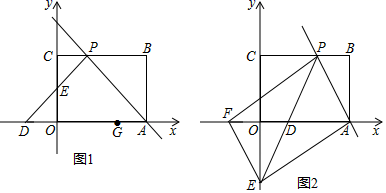
23.(10分)如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
24.(12分)如图,反比例函数的图象经过点![]()
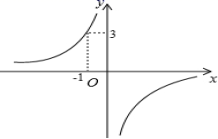
(1)求该反比例函数的解析式;
(2)当![]() 时,根据图象请直接写出自变量
时,根据图象请直接写出自变量![]() 的取值范围.
的取值范围.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、B
4、A
5、C
6、D
7、D
8、A
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、﹣1.
12、40°。
13、1.
14、1
15、1.
16、1.
三、解下列各题(本大题共8小题,共72分)
17、(1)详见解析;(2)![]()
18、至少购进玫瑰200枝.
19、(1)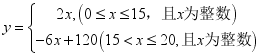 ;(2)200元,270元;(3)“最佳销售期”共有5天,销售单价最高为9.6元 .
;(2)200元,270元;(3)“最佳销售期”共有5天,销售单价最高为9.6元 .
20、3.
21、(1)![]() 点坐标为
点坐标为![]() ;(2)
;(2)![]() ;(3)点E的坐标为
;(3)点E的坐标为![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() .
.
22、不等式组的整数解为0、1、2、1.
23、(1)①y=﹣x+3,②N(0,![]() ),
),![]() ;(2) y=2x﹣2.
;(2) y=2x﹣2.
24、(1)![]() (2)
(2)![]() 或
或![]()
相关试卷
这是一份2023-2024学年江苏省东台市第六联盟九上数学期末质量检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,抛物线的对称轴是等内容,欢迎下载使用。
这是一份2023-2024学年江苏省东台市第六教育联盟数学九上期末统考试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,一元二次方程的一次项系数是等内容,欢迎下载使用。
这是一份江苏省东台市第六教育联盟2023-2024学年八年级数学第一学期期末检测试题含答案,共8页。试卷主要包含了在平面直角坐标系中,点M,一次函数的图象与轴的交点坐标是等内容,欢迎下载使用。












