


江苏省南京一中学2022-2023学年七下数学期末学业质量监测模拟试题含答案
展开江苏省南京一中学2022-2023学年七下数学期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.在平行四边形ABCD中,∠A:∠B:∠C:∠D的可能情况是( )
A.2:7:2:7 B.2:2:7:7 C.2:7:7:2 D.2:3:4:5
2.如图,在△ABC中,点D、E、F分别在BC、AB、CA上,且DE∥CA,DF∥BA,则下列三种说法:
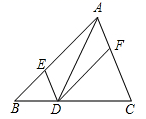
(1)如果∠BAC=90°,那么四边形AEDF是矩形
(2)如果AD平分∠BAC,那么四边形AEDF是菱形
(3)如果AD⊥BC且AB=AC,那么四边形AEDF是正方形 .其中正确的有 ( )
A.3个 B.2个 C.1个 D.0个
3.若一元二次方程![]() 有实数根,则实数
有实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,在平行四边形ABCD中,BE=2,AD=8,DE平分∠ADC,则平行四边形的周长为( )
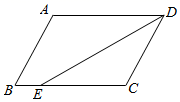
A.14 B.24 C.20 D.28
5.平行四边形边长为![]() 和
和![]() ,其中一内角平分线把边长分为两部分,这两部分是( )
,其中一内角平分线把边长分为两部分,这两部分是( )
A.![]() 和
和![]() B.
B.![]() 和
和![]() C.
C.![]() 和
和![]() D.
D.![]() 和
和![]()
6.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:华、爱、我、中、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.我爱美 B.中华游 C.爱我中华 D.美我中华
7.已知反比例函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.其图象分别位于第一、三象限
B.当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
C.若点![]() 在它的图象上,则点
在它的图象上,则点![]() 也在它的图象上
也在它的图象上
D.若点![]() 都在该函数图象上,且
都在该函数图象上,且![]() ,则
,则![]()
8.矩形、菱形、正方形都一定具有的性质是( )
A.邻边相等 B.四个角都是直角
C.对角线相等 D.对角线互相平分
9.如图,在△ABC中,点D、E分别是边AB、AC上的点,且DE∥BC,若![]() ,DE=3,则BC的长度是( )
,DE=3,则BC的长度是( )
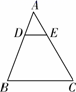
A.6 B.8 C.9 D.10
10.点A、B、C、D在同一平面内,从AB∥CD,AB=CD,AD∥BC这三条件中任选两个能使四边形ABCD是平行四边形的选法有( )
A.1种 B.2种 C.3种 D.以上都不对
二、填空题(本大题共有6小题,每小题3分,共18分)
11.命题“两直线平行,同位角相等”的逆命题是 .
12.直角三角形两边长为5和12,则此直角三角形斜边上的中线的长是_______.
13.计算:![]() __.
__.
14.设![]() 、
、![]() 是方程
是方程![]() 的两个实数根,则
的两个实数根,则![]() 的值为_____.
的值为_____.
15.已知平行四边形ABCD中,![]() ,
,![]() ,AE为BC边上的高,且
,AE为BC边上的高,且![]() ,则平行四边形ABCD的面积为________.
,则平行四边形ABCD的面积为________.
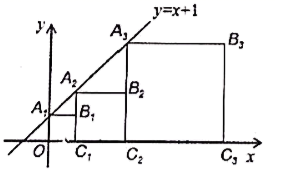
16.正方形![]() ,
,![]() ,
,![]() ,...按如图的方式放置,点
,...按如图的方式放置,点![]() ,
,![]() ,
,![]() ...和点
...和点![]() ,
,![]() ,
,![]() ...分别在直线
...分别在直线![]() 和
和![]() 轴上,则点
轴上,则点![]() 的坐标为_______.
的坐标为_______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.在这10名工人中,如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适.
18.(8分)某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
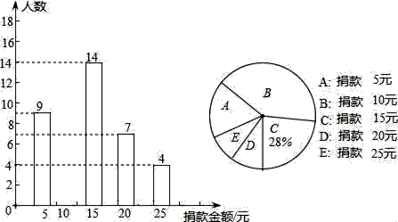
(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 平均数是 中位数为
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
19.(8分)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F
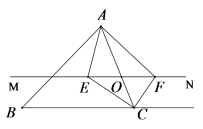
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
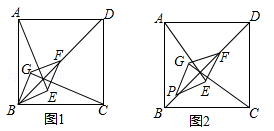
20.(8分)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
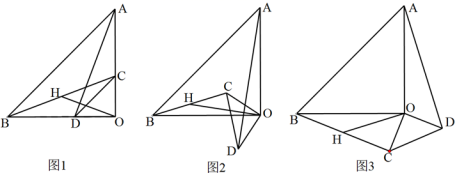
(1)如图1所示,求证:![]() 且
且![]()
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论
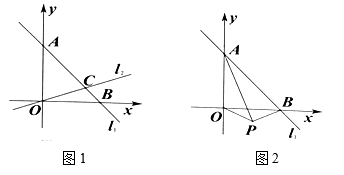
21.(8分)已知:如图1,在平面直角坐标系中,直线![]() 与坐标轴分别相交于点
与坐标轴分别相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若平行于![]() 轴的直线
轴的直线![]() 交于直线
交于直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)如图2,点![]() 是第四象限内一点,且
是第四象限内一点,且![]() ,连接
,连接![]() ,探究
,探究![]() 与
与![]() 之间的位置关系,并证明你的结论.
之间的位置关系,并证明你的结论.
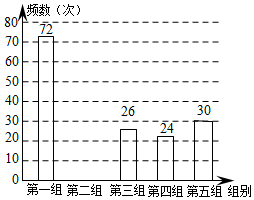
22.(10分)某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
组别 | 单次营运里程“x”(千米) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据以上信息,解答下列问题:
(1)表中a= ,样本中“单次营运里程”不超过15千米的频率为 ;
(2)请把频数分布直方图补充完整;
(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)
23.(10分)探索与发现
(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,只写出猜想不需证明.
24.(12分)某学校打算招聘英语教师。对应聘者进行了听、说、读、写的英语水平测试,其中甲、乙两名应聘者的成绩(百分制)如下表所示。

(1)如果学校想招聘说、读能力较强的英语教师,听、说、读、写成绩按照2:4:3:1的比确定,若在甲、乙两人中录取一人,请计算这两名应聘者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
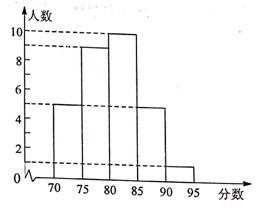
(2)学校按照(1)中的成绩计算方法,将所有应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最后左边一组分数![]() 为:
为:![]() )。
)。
①参加该校本次招聘英语教师的应聘者共有______________人(直接写出答案即可)。
②学校决定由高分到低分录用3名教师,请判断甲、乙两人能否被录用?并说明理由。
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、D
4、D
5、C
6、C
7、C
8、D
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、同位角相等,两直线平行
12、6或6.5
13、-![]()
14、-1
15、2或1
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、6名.
18、(1)50人,补图见解析;(2)10,13.1,12.5;(3)132人
19、 (1)见解析;(2) 当O运动到OA=OC处,四边形AECF是矩形.理由见解析.
20、(1)详见解析;(2)详见解析.
21、(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,理由见解析。
,理由见解析。
22、 (1)48,0.1;(2)见解析;(3)750次.
23、(1)结论:AE=CG.理由见解析;(2)结论不变,AE=CG.
24、(1)录取乙;(2)①30,②乙一定能被录用;甲不一定能被录用,见解析.
江苏省宝应县山阳中学2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份江苏省宝应县山阳中学2022-2023学年七下数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了如果,下列各式中不正确的是,下列变形错误的是,下列二次拫式中,最简二次根式是等内容,欢迎下载使用。
江苏省南京雨花台区七校联考2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份江苏省南京雨花台区七校联考2022-2023学年七下数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列式子中为最简二次根式的是,某校八年级班体训队员的身高如下等内容,欢迎下载使用。
江苏省南京市致远中学2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份江苏省南京市致远中学2022-2023学年七下数学期末学业质量监测模拟试题含答案,共8页。试卷主要包含了下列计算过程中,结果是2的是等内容,欢迎下载使用。












