


江苏省徐州市市区部分2022-2023学年七下数学期末经典模拟试题含答案
展开江苏省徐州市市区部分2022-2023学年七下数学期末经典模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.关于![]() 的方程
的方程![]() 有实数根,则
有实数根,则![]() 满足( )
满足( )
A.![]() B.
B.![]() 且
且![]() C.
C.![]() 且
且![]() D.
D.![]()
2.在学校举行的“阳光少年,励志青年”的演讲比赛中,五位评委给选手小明的评分分别为:90,85,90,80,95,则这组数据的众数是( )
A.95 B.90 C.85 D.80
3.某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩![]() 及其方差
及其方差![]() 如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
| 甲 | 乙 | 丙 | 丁 | |
| 8 | 9 | 9 | 8 | |
| 1 | 1 | 1.2 | 1.3 |
A.甲 B.乙 C.丙 D.丁
4.某学习小组7名同学在一学期里阅读课外书籍的册数分别是:14,12,13,12,17,18,16,则这组数据中位数是( )
A.12 B.13 C.14 D.17
5.如图,已知四边形ABCD的对角线AC⊥BD,则顺次连接四边形ABCD各边中点所得的四边形是( )
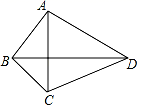
A.矩形 B.菱形 C.正方形 D.平行四边形
6.如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,依次作正方形
,依次作正方形![]() 、正方形
、正方形![]() 、…正方形
、…正方形![]() 使得点
使得点![]() 、
、![]() 、…,
、…,![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、…,
、…,![]() 在
在![]() 轴上,则点
轴上,则点![]() 的坐标是( )
的坐标是( )
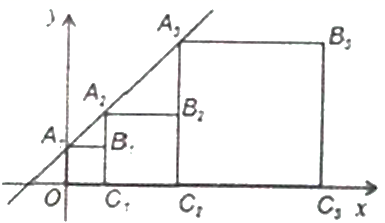
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.如图所示,在四边形![]() 中,
中,![]() ,要使四边形
,要使四边形![]() 成为平行四边形还需要条件( )
成为平行四边形还需要条件( )
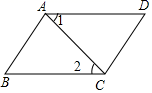
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.一同学将方程![]() 化成了
化成了![]() 的形式,则m、n的值应为( )
的形式,则m、n的值应为( )
A.m=1.n=7 B.m=﹣1,n=7 C.m=﹣1,n=1 D.m=1,n=﹣7
9.若一元二次方程ax2+bx+c=0(a≠0)有一个根为-1,则a-b+c的值是( )
A.-1![]() B.1 C.0 D.不能确定
B.1 C.0 D.不能确定
10.如图,在平行四边形ABCD中,AC、BD相交于点O,点E是AB的中点.若OE=3cm,则AD的长是( )
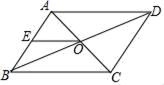
A.3cm B.6cm C.9cm D.12cm
二、填空题(本大题共有6小题,每小题3分,共18分)
11.公路全长为skm,骑自行车t小时可到达,为了提前半小时到达,骑自行车每小时应多走_____________.
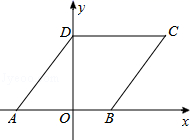
12.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是_______.
13.如图,折叠矩形纸片的一边AD,使点D落在BC边上的点F处,BC=10cm, AB=8cm, 则EC的长为_________.

14.等腰三角形的两条中位线分别为3和5,则等腰三角形的周长为_____.
15.已知一次函数![]() (
(![]() 为常数,且
为常数,且![]() ).若当
).若当![]() 时,函数有最大值7,则
时,函数有最大值7,则![]() 的值为_____.
的值为_____.
16.如果关于![]() 的不等式组
的不等式组![]() 的整数解仅有
的整数解仅有![]() ,
,![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有_______个;如果关于
共有_______个;如果关于![]() 的不等式组
的不等式组![]() (其中
(其中![]() ,
,![]() 为正整数)的整数解仅有
为正整数)的整数解仅有![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有______个.(请用含
共有______个.(请用含![]() 、
、![]() 的代数式表示)
的代数式表示)
三、解下列各题(本大题共8小题,共72分)
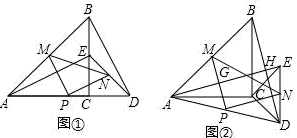
17.(8分)如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.
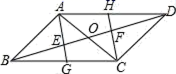
18.(8分)如图,在▱ABCD中,对角线AC,BD交于点O,点E,点F在BD上,且 BE=DF 连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:△AOE≌△COF;
(2)若AC平分∠HAG,求证:四边形AGCH是菱形.
19.(8分)某市某水果批发市场某批发商原计划以每千克10元的单价对外批发销售某种水果.为了加快销售,该批发商对价格进行两次下调后,售价降为每千克6.4元.
(1)求平均每次下调的百分率;
(2)某大型超市准备到该批发商处购买2吨该水果,因数量较多,该批发商决定再给予两种优惠方案以供选择.方案一:打八折销售;方案二:不打折,每吨优惠现金1000元.试问超市采购员选择哪种方案更优惠?请说明理由.
20.(8分)解方程:
(1)2x2﹣3x+1=1.
(2)x2﹣8x+1=1.(用配方法)
21.(8分)如图,一次函数y=k2x+b的图象与y轴交于点B,与正比例函数y=k1x的图象相交于点A(4,3),且OA=OB.
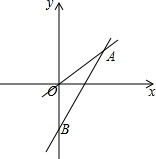
(1)分别求出这两个函数的解析式;
(2)求△AOB的面积;
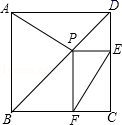
22.(10分)已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
求证:AP=EF.
23.(10分)下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
24.(12分)某班开展勤俭节约的活动,对每个同学的一天的消费情况进行调查,得到统计图如图所示:
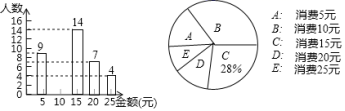
(1)求该班的总人数;
(2)将条形图补充完整,并写出消费金额的中位数;
(3)该班这一天平均每人消费多少元?
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、B
4、C
5、A
6、D
7、B
8、B
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() -
-![]()
12、(5,4).
13、3cm
14、22或1.
15、a=2或a=-3.
16、6 pq
三、解下列各题(本大题共8小题,共72分)
17、 (1)证明见解析;(2)成立,理由见解析.
18、 (1)见解析;(2) 见解析.
19、(1)平均每次下调的百分率是![]() ;(2)超市采购员选择方案一购买更优惠.
;(2)超市采购员选择方案一购买更优惠.
20、(1)x1=![]() ,x2=1;(2)x1=4+
,x2=1;(2)x1=4+![]() ,x2=4﹣
,x2=4﹣![]()
21、(1)y=![]() x,y=2x-5(2)10
x,y=2x-5(2)10
22、见试题解析
23、(1)90分;90分;(2)86分;(3)91.2分.
24、(1)50;(2)图详见解析,12.5;(3)该班这一天平均每人消费13.1元.
江苏省徐州市区部分2023-2024学年数学九上期末综合测试模拟试题含答案: 这是一份江苏省徐州市区部分2023-2024学年数学九上期末综合测试模拟试题含答案,共8页。试卷主要包含了若,则等于等内容,欢迎下载使用。
2023-2024学年江苏省徐州市区部分数学九上期末考试模拟试题含答案: 这是一份2023-2024学年江苏省徐州市区部分数学九上期末考试模拟试题含答案,共8页。试卷主要包含了抛物线 的顶点坐标是等内容,欢迎下载使用。
2023-2024学年江苏省徐州市区部分数学八上期末监测模拟试题含答案: 这是一份2023-2024学年江苏省徐州市区部分数学八上期末监测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,若是完全平方式,则m的值等于,有下列实数等内容,欢迎下载使用。












