


江苏省扬州教育院附属中学2022-2023学年七年级数学第二学期期末学业质量监测试题含答案
展开
这是一份江苏省扬州教育院附属中学2022-2023学年七年级数学第二学期期末学业质量监测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,尺规作图要求等内容,欢迎下载使用。
江苏省扬州教育院附属中学2022-2023学年七年级数学第二学期期末学业质量监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题(每小题3分,共30分)1.将一次函数![]() 图像向下平移
图像向下平移![]() 个单位,与双曲线
个单位,与双曲线![]() 交于点A,与
交于点A,与![]() 轴交于点B,则
轴交于点B,则![]() =( )A.
=( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.矩形各内角的平分线能围成一个( )A.矩形 B.菱形 C.等腰梯形 D.正方形3.若一个多边形从一个顶点出发的对角线共有3条,则这个多边形的内角和为( )A.360° B.540° C.720° D.1080°4.如图,海平面上,有一个灯塔分别位于海岛A的南偏西30°和海岛B的南偏西60°的方向上,则该灯塔的位置可能是( )
2.矩形各内角的平分线能围成一个( )A.矩形 B.菱形 C.等腰梯形 D.正方形3.若一个多边形从一个顶点出发的对角线共有3条,则这个多边形的内角和为( )A.360° B.540° C.720° D.1080°4.如图,海平面上,有一个灯塔分别位于海岛A的南偏西30°和海岛B的南偏西60°的方向上,则该灯塔的位置可能是( )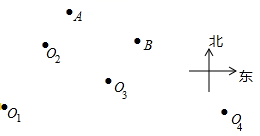 A.O1 B.O2 C.O3 D.O45.某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
A.O1 B.O2 C.O3 D.O45.某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )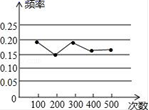 A.在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”B.从一副扑克牌中任意抽取一张,这张牌是“红色的”C.掷一枚质地均匀的硬币,落地时结果是“正面朝上”D.掷一个质地均匀的正六面体骰子,落地时面朝上的点数是66.尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.如图是按上述要求排乱顺序的尺规作图:
A.在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”B.从一副扑克牌中任意抽取一张,这张牌是“红色的”C.掷一枚质地均匀的硬币,落地时结果是“正面朝上”D.掷一个质地均匀的正六面体骰子,落地时面朝上的点数是66.尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.如图是按上述要求排乱顺序的尺规作图: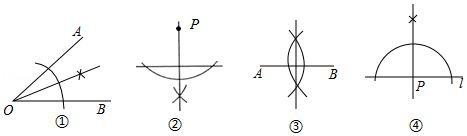 则正确的配对是( )A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣ⅠC.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ7.某校举办“汉字听写大赛”,7名学生进入决赛,他们所得分数互不相同,比赛共设3个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )A.平均数 B.中位数 C.众数 D.方差8.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
则正确的配对是( )A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣ⅠC.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ7.某校举办“汉字听写大赛”,7名学生进入决赛,他们所得分数互不相同,比赛共设3个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )A.平均数 B.中位数 C.众数 D.方差8.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )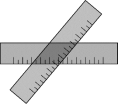 A.矩形 B.菱形 C.正方形 D.无法判断9.若菱形的周长为8,高为1,则菱形两邻角的度数比为( )A.3∶1 B.4∶1 C.5∶1 D.6∶110.如图, 四边形ABCD的对角线AC,BD相交于点O,E是AB中点,且AE+EO=4,则四边形ABCD的周长为( )
A.矩形 B.菱形 C.正方形 D.无法判断9.若菱形的周长为8,高为1,则菱形两邻角的度数比为( )A.3∶1 B.4∶1 C.5∶1 D.6∶110.如图, 四边形ABCD的对角线AC,BD相交于点O,E是AB中点,且AE+EO=4,则四边形ABCD的周长为( )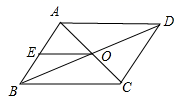 A.32 B.16 C.8 D.4二、填空题(本大题共有6小题,每小题3分,共18分)11.已知菱形ABCD的对角线AC=10,BD=24,则菱形ABCD的面积为__________。12.若方程
A.32 B.16 C.8 D.4二、填空题(本大题共有6小题,每小题3分,共18分)11.已知菱形ABCD的对角线AC=10,BD=24,则菱形ABCD的面积为__________。12.若方程![]() +2=
+2=![]() 的解是正数,则m的取值范围是___.13.分解因式:
的解是正数,则m的取值范围是___.13.分解因式:![]() .14.四边形的外角和等于 .15.一副常规的直角三角板如图放置,点
.14.四边形的外角和等于 .15.一副常规的直角三角板如图放置,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ______.
______.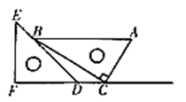 16.分式
16.分式![]() 与
与![]() 的最简公分母是__________.三、解下列各题(本大题共8小题,共72分)17.(8分)已知1<x<2,
的最简公分母是__________.三、解下列各题(本大题共8小题,共72分)17.(8分)已知1<x<2,![]() ,则
,则![]() 的值是_____. 18.(8分)如图,在平面直角坐标系中,已知A(-3,-4),B(0,-2).(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.
的值是_____. 18.(8分)如图,在平面直角坐标系中,已知A(-3,-4),B(0,-2).(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.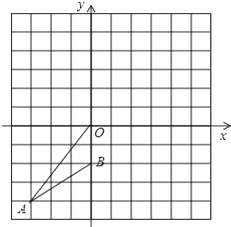 19.(8分)已知一次函数
19.(8分)已知一次函数![]() 的图象过点
的图象过点![]() ,
,![]() .(1)求此函数的表达式;(2)若点
.(1)求此函数的表达式;(2)若点![]() 在此函数的图象上,求
在此函数的图象上,求![]() 的值. 20.(8分)如图,矩形
的值. 20.(8分)如图,矩形![]() 的面积为20cm2,对角线交于点
的面积为20cm2,对角线交于点![]() ,以AB、AO为邻边作平行四边形
,以AB、AO为邻边作平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形![]() 的面积为______,平行四边形
的面积为______,平行四边形![]() 的面积为______.
的面积为______.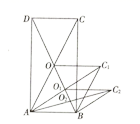 21.(8分)
21.(8分)![]() 是正方形
是正方形![]() 的边
的边![]() 上一动点(不与
上一动点(不与![]() 重合),
重合), ![]() ,垂足为
,垂足为![]() ,将
,将![]() 绕点
绕点![]() 旋转,得到
旋转,得到![]() ,当射线
,当射线![]() 经过点
经过点![]() 时,射线
时,射线![]() 与
与![]() 交于点
交于点![]() .
.![]() 求证:
求证:![]() ;
; ![]() 在点
在点![]() 的运动过程中,线段
的运动过程中,线段![]() 与线段
与线段![]() 始终相等吗?若相等请证明;若不相等,请说明理由.
始终相等吗?若相等请证明;若不相等,请说明理由.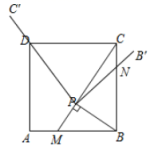 22.(10分)已知T
22.(10分)已知T![]() .(1)化简T;(2)若正方形ABCD的边长为a,且它的面积为9,求T的值. 23.(10分)如图,直线
.(1)化简T;(2)若正方形ABCD的边长为a,且它的面积为9,求T的值. 23.(10分)如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的横坐标为3.
的横坐标为3.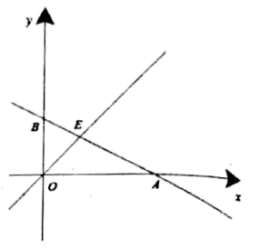 (1)直接写出
(1)直接写出![]() 值________;(2)当
值________;(2)当![]() 取何值时,
取何值时,![]() ?(3)在
?(3)在![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的值. 24.(12分)如图①,在平面直角坐标系中,直线
的值. 24.(12分)如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.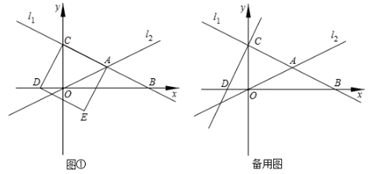 (1)求出
(1)求出![]() 三点的坐标.(2)求直线
三点的坐标.(2)求直线![]() 的函数表达式.(3)在(2)的条件下,点
的函数表达式.(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、B2、D3、C4、A5、D6、D7、B8、B9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、12012、m<3且m≠2.13、
的坐标;若不存在,请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、B2、D3、C4、A5、D6、D7、B8、B9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、12012、m<3且m≠2.13、![]() .14、360°.15、
.14、360°.15、![]() 16、
16、![]() 三、解下列各题(本大题共8小题,共72分)17、2.18、(1)画图见解析,A1(3,4),B1(0,2);(2)以A、B、A1、B1为顶点的四边形为平行四边形,理由见解析.19、(1)y=
三、解下列各题(本大题共8小题,共72分)17、2.18、(1)画图见解析,A1(3,4),B1(0,2);(2)以A、B、A1、B1为顶点的四边形为平行四边形,理由见解析.19、(1)y=![]() x+3;(2)a=4;
x+3;(2)a=4;
20、![]()
![]() 21、
21、![]() 见解析;
见解析;![]()
![]() ,证明见解析22、(1)
,证明见解析22、(1)![]() ;(2)
;(2)![]() .23、(1)
.23、(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)
;(3)![]() 或
或![]() .24、(1)
.24、(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,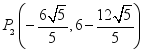 ,
,![]() .
.
相关试卷
这是一份2023-2024学年江苏省扬州教育院附属中学九年级数学第一学期期末联考模拟试题含答案,共8页。试卷主要包含了下列函数中是反比例函数的是等内容,欢迎下载使用。
这是一份江苏省扬州教育院附属中学2023-2024学年数学九年级第一学期期末学业水平测试试题含答案,共7页。试卷主要包含了关于的一元二次方程,则的条件是等内容,欢迎下载使用。
这是一份北京市教育院附属中学2023-2024学年数学九上期末学业质量监测试题含答案,共7页。








