人教版九年级上册22.1.2 二次函数y＝ax2的图象和性质教案

这是一份人教版九年级上册22.1.2 二次函数y＝ax2的图象和性质教案，共6页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。
第二十二章 二次函数22.1二次函数的图象和性质22.1.2   二次函数y=ax2的图象和性质一、教学目标1．正确理解抛物线的有关概念.2．会用描点法画出二次函数y=ax²的图象，概括出图象的特点.3．掌握形如y=ax²的二次函数图象的性质，并会应用．二、教学重难点重点：正确理解抛物线的有关概念.难点：会用描点法画出二次函数y=ax²的图象，概括出图象的特点，掌握形如y=ax²的二次函数图象的性质，并会应用．                                                   三、教学过程【新课导入】[复习导入]问题1：1.二次函数的定义？      一般地，形如 y=ax2+bx+c（a,b,c是常数，a≠0）的函数，叫做二次函数.                                   问题2:一次函数的图象是一条直线，二次函数的图象是什么形状？如何画一个二次函数的图象？【新知探究】（一）二次函数y=ax2的图象先画二次函数 y=x2 的图象.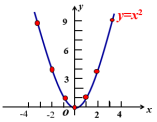[课件展示]1.列表：  在y = x2 中自变量x可以是任意实数，列表表示几组对应值：x…-3-2-10123…y=x2…9410149…2. 描点：根据表中x,y的数值在坐标平面中描点（x,  y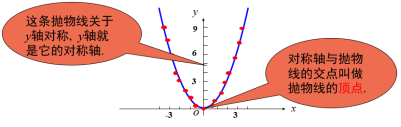）3. 连线：如图，再用平滑曲线顺次连接各点，就得到y = x2 的图象．      二次函数y=x2的图象类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上.我们把它叫做抛物线.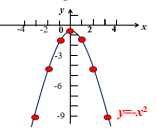[思考]画出函数y=-x2的图象.x…-3-2-10123…y=x2…-9-4-10-1-4-9…  （二）二次函数y=ax2的性质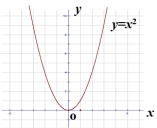[讨论交流]1.利用你前面学习的函数图象的性质，说说二次函数y=x2的图象有哪些性质，并与同伴交流.[归纳总结]（1）y＝x2是一条抛物线; （2）图象开口向上;（3）图象关于y轴对称;（4）顶点（0 ，0）;（5）图象有最低点．[讨论交流]2.说说二次函数y=-x2的图象有哪些性质,与同伴交流.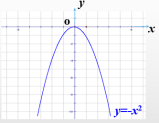[归纳总结]（1）y＝-x2是一条抛物线;（2）图象开口向下;（3）图象关于y轴对称;（4）顶点（ 0 ，0 ）;（5）图象有最高点．[归纳总结]二次函数y=ax2 的图象性质：（1）y＝ax2是一条抛物线;（2）顶点都在原点; （3）图像关于y轴对称; （4）当a>0时，开口向上；  当a<0时，开口向下．[深入思考]观察下列图象，抛物线y=ax2与y=-ax2（a＞0)的关系是什么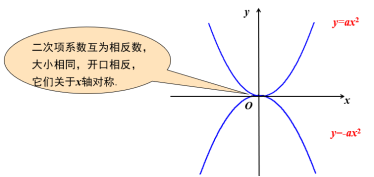？[思考]问题1：观察图形，y随x的变化如何变化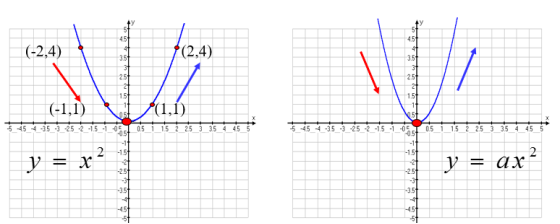？[归纳总结]对于抛物线 y = ax 2 （a＞0） 当x＞0时，y随x取值的增大而增大； 当x<0时，y随x取值的增大而减小.[思考]问题2：观察图形，y随x的变化如何变化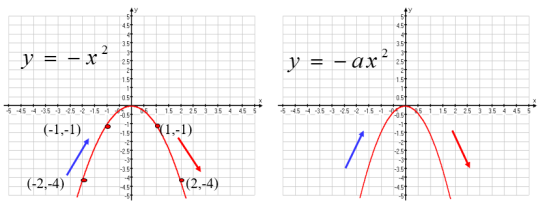？[归纳总结]对于抛物线 y = ax 2 （a＜0）当x＞0时，y随x取值的增大而减小；当x<0时，y随x取值的增大而增大.例1 在同一直角坐标系中，画出函数 的图象．解：分别列表，再画出它们的图象，如图x…-4-3-2-101234…y=x2…84.520.500.524.58… x…-2-1.5-1-0.500.511.52…y=x2…84.520.500.524.58…  [思考]二次函数 开口大小与a的大小有什么关系？当a>0时，a越大，开口越小.[思考]在同一直角坐标系中，画出函数的图象．x…-4-3-2-101234…y=x2…-8-4.5-2-0.50-0.5-2-4.5-8… x…-2-1.5-1-0.500.511.52…y=x2…-8-4.5-2-0.50-0.5-2-4.5-8…[思考] 二次函数 开口大小与a的大小有什么关系？当a<0时，a越小（即a的绝对值越大），开口越小.[课件展示]y=ax2 (a≠0)a>0a<0图象开口方向向上向下顶点坐标(0 ,0)(0 ,0)对称轴y轴y轴增减性当x<0时，y随着x的增大而减小；当x>0时，y随着x的增大而增大.当x<0时,y随着x的增大而增大；当x>0时，y随着x的增大而减小.最值x=0时,y最小=0x=0时,y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小；|a|越小,抛物线的开口就越大.例2  已知 y =(m+1)x m2+m是二次函数,且其图象开口向上,求m的值和函数解析式.解: 依题意有:解②得m1=－2, m2=1；由①得m>－1.∴ m=1.此时,二次函数解析式为: y=2x2.例3  已知二次函数y=x2．（1）判断点A（2，4）在二次函数图象上吗？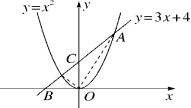（2）请分别写出点A关于x轴的对称点B的坐标，关于y轴的对称点C的坐标，关于原点O的对称点D的坐标.解：（1）当x=2时，y=x2=4，所以A（2，4）在二次函数图象上；（2）点A关于x轴的对称点B的坐标为（2，-4），点A关于y轴的对称点C的坐标为（-2，4），点A关于原点O的对称点D的坐标为（-2，-4）；【课堂小结】二次函数y=ax2的图象及性质y=ax2 (a≠0)a>0a<0图象开口方向向上向下顶点坐标(0 ,0)(0 ,0)对称轴y轴y轴增减性当x<0时，y随着x的增大而减小；当x>0时，y随着x的增大而增大.当x<0时,y随着x的增大而增大；当x>0时，y随着x的增大而减小.最值x=0时,y最小=0x=0时,y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小；|a|越小,抛物线的开口就越大.【课堂训练】1.函数y=2 x 2的图象的开口 向上    ，对称是  y轴   ，顶点是   （0,0）   ；在对称轴的左侧，y随x的增大而  减小     ，在对称轴的右侧，y随x的增大而   增大  .2.函数y=-3 x 2的图象的开口   向下  ，对称轴是  y轴   ，顶点 （0,0）   ；在对称轴的左侧，y随x的增大而   增大   ，在对称轴的右侧，y随x的增大而  减小   .3.已知 是二次函数，且当x＞0时，y随x增大而增大，则k=  2  .4.若抛物线 y =a x 2 （a ≠ 0），过点（-1，2）.  （1）a的值是    2   ；对称轴是     y轴    ，开口    向上    ；  （2）顶点坐标是  （0,0）    ，顶点是抛物线上的最  小 值 ，抛物线在x轴的   上   方（除顶点外）；   (3) 若A（ x 1, y 1),B(x 2, y 2)在这条抛物线上，且x 1< x 2<0, 则y 1  >   y 2.[拓广探索]5.已知：如图，直线y＝3x＋4与抛物线y＝x2交于A、B两点，求出A、B两点的坐标，并求出两交点与原点所围成的三角形的面积．解：由题意得      解得或所以此两函数的交点坐标为A(4，16)和B(－1，1)．∵直线y＝3x＋4与y轴相交于点C(0，4)，即CO＝4.∴S△ACO＝·CO·4＝8，S△BOC＝ ×4×1＝2，∴S△ABO＝S△ACO＋S△BOC＝10.【布置作业】 【教学反思】教学过程中，强调学生自主探索和合作交流，在操作中探究二次函数y＝ax2的图象与性质，体会数学建模的数形结合的思想方法.