人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.4 二次函数y＝ax2＋bx＋c的图象和性质第1课时教学设计

这是一份人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.4 二次函数y＝ax2＋bx＋c的图象和性质第1课时教学设计，共7页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。
第二十二章 二次函数22.1 二次函数的图象和性质22.1.3  二次函数y=ax2+bx+c的图象和性质第1课时 二次函数y=ax2+bx+c的图象和性质一、教学目标1.会用配方法或公式法将一般式y＝ax2＋bx＋c化成顶点式y=a(x-h)2+k.2.能够熟练求出二次函数一般式y＝ax2＋bx＋c的顶点坐标、对称轴.二、教学重难点重点：求出二次函数一般式y＝ax2＋bx＋c的顶点坐标、对称轴.难点：会用配方法或公式法将一般式y＝ax2＋bx＋c化成顶点式y=a(x-h)2+k.三、教学过程【新课导入】二次函数y=a(x-h)2+k的图象与性质y=a(x-h)2+k a>0 a<0     函数图象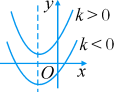  h>0 h<0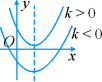开 口 方 向向上向下对 称 轴直线 x=h直线 x=h顶 点 坐 标（h,k）（h,k）函数的增减性当x<h时，y随x增大而减小；当x>h时，y随x增大而增大.当x<h时，y随x增大而增大；当x>h时，y随x增大而减小.最  值x=h时，y最小值=kx=h时，y最大值=k [思考]我们已经知道y=a(x-h)2+k的图象和性质，能否利用这些知识来讨论二次函数                                         y= x2-6x+21的图象和性质？[思考]怎样将y= x2-6x+21化成y=a(x-h)2+k的形式？配方可得y= x2-6x+21=（x2-12x+42）=（x2-12x+62-62+42）=[（x2-12x+62）-62+42]=[（x-6）2+6]=（x-6）2+3y= x2-6x+21你知道是怎样配方的吗？                             (1)“提”：提出二次项系数；                             (2)“配”：括号内配成完全平方；                             (3)“化”：化成顶点式.y=（x-6）2+3[思考]你能说出y=（x-6）2+3的对称轴及顶点坐标吗？对称轴是直线x=6,顶点坐标是（6，3）.[思考]二次函数y =（x-6）2+3可以看作是由y= x2怎样平移得到的？平移方法1：    先向上平移3个单位，再向右平移6个单位得到的；平移方法2：先向右平移6个单位，再向上平移3个单位得到的.[思考] 如何画二次函数 y= x2-6x+21的图象？列表：利用图像的对称性，选取适当值列表计算.x…3456789…y =（x-6）2+3…7.553.533.557.5… 然后描点画图，得到图象如右图.[思考]结合二次函数y= x2-6x+21的图象，说说其性质.对称轴左侧，抛物线从左到右下降；对称轴右侧，抛物线从左到右上升.当x<6时，y随x的增大而减小；当x>6时，y随x的增大而增大；当x=6时，y有最小值3.探究：画出函数y=- x2 +x- 的图象，并说明这个函数具有哪些性质.解: 函数y=- x2 +x- 通过配方可得y=- （x-1）2-2                 ，先列表：x…-2-101234…y…-6.5-4-2.5-2-2.5-4-6.5…然后描点、连线，得到图象如下图.由图象可知，这个函数具有如下性质：当x＜1时，函数值y随x的增大而增大；当x＞1时，函数值y随x的增大而减小；当x=1时，函数取得最大值，最大值y=-2.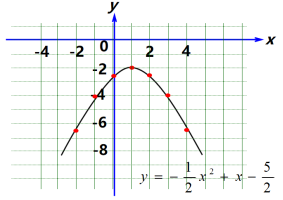[思考]我们如何用配方法将一般式y=ax2+bx+c（a≠0)化成y=a(x-h)2+k的形式？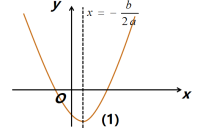y=ax2+bx+c =a[x2+x+（）2-（）2]+c=a[x2+x+（）2-（）2]+c=a[x2+x+（）2-（）2]+c=a（x+）2- +c=a（x+）2+ [归纳总结]二次函数y=ax2+bx+c的图象和性质一般地，二次函数y=ax2+bx+c的可以通过配方化成y=a(x-h)2+k的形式，即y=ax2+bx+c=a（x+）2+ 因此，抛物线y=ax2+bx+c 的对称轴是x=-.顶点是：（-，） 如果a>0,当x<-时，y随x的增大而减小；当x>-时，y随x的增大而增大.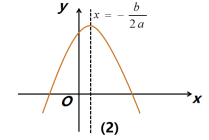如果a<0,当x<-时，y随x的增大而增大；当x>-时，y随x的增大而减小.[思考]二次函数y=ax2+bx+c的图象如下图所示，请根据二次函数的性质填空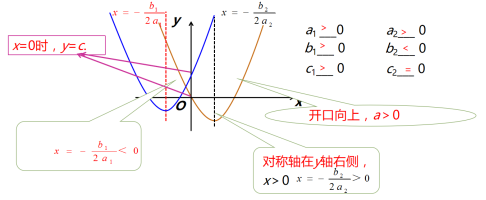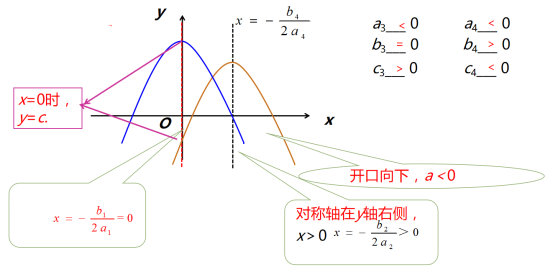：二次函数y=ax2+bx+c的图象与a、b、c的关系字母符号图象的特征a＞0开口向上a＜0开口向下b=0对称轴为y轴a、b同号对称轴在y轴的左侧a、b异号对称轴在y轴的右侧c=0经过原点c＞0与y轴交于正半轴c＜0与y轴交于负半轴 [思考] 已知二次函数y=ax2+bx+c的图象如图所示，下列结论：①abc＞0；②2a－b＜0；③4a－2b＋c＜0；④(a＋c)2＜b2. 其中正确的个数是(　D　)A．1　　          　B．2　　 　     　C．3　       　　D．4[分析]由图象开口向下可得a＜0，由对称轴在y轴左侧可得b＜0，由图象与y轴交于正半轴可得c＞0，则abc＞0，故①正确；由对称轴x>－1可得2a－b＜0，故②正确； 由图象上横坐标为 x＝－2的点在第三象限可得4a－2b＋c＜0，故③正确；由图象上x＝1的点在第四象限得a＋b＋c＜0，由图象上x＝－1的点在第二象限得出 a－b＋c＞0，则(a＋b＋c)(a－b＋c)＜0，即(a＋c)2－b2＜0，可得(a＋c)2＜b2，故④正确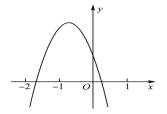．[思考] 如图，二次函数y＝ax2－bx＋２的大致图象如图所示，则函数y ＝－ax＋b的图象不经过（  C  ）A．第一象限       B．第二象限        C．第三象限          D．第四象限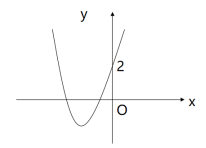【课堂小结】函数y=ax2+bx+c的图象和性质抛物线y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)顶点坐标(-，）(-，）对称轴直线x=-直线x=-位置由a,b和c的符号确定由a,b和c的符号确定开口方向向上向下 增减性在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧, y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧, y随着x的增大而减小.最值 当x=-时，最小值为当x=-时，最大值为【课堂训练】1.填空 顶点坐标对称轴最值y=-x2+2x(1, 3)x=1最大值1y=-2x2-1(0, -1)y轴最大值-1y=9x2+6x-5( - ,-6)x= - 最小值-62.填空：二次函数y=-2x2-4x+1的图象和性质①               将函数y=-2x2-4x+1化成y＝a(x－h)2＋k的形式是y=-2（x+1）2+3；②               抛物线的开口方向是向下，顶点坐标是(-1，3)，对称轴是直线x＝-1；③               当x＝-1时，函数取得最大值为3；④               当x大于-1时，y随x的增大而减小，当x小于-1时，y随x的增大而增大；⑤               抛物线y=-2x2-4x+1可由抛物线y=-2x2向左(或上)平移1(或3)个单位长度，再向上(或左)平移3(或1)个单位长度得到．中考链接1.（2020•百色）将抛物线y＝（x+1）2+1平移，使平移后得到抛物线y＝x2+6x+6．则需将原抛物线（  B  ）A．先向左平移1个单位长度，再向上平移5个单位长度 B．先向左平移2个单位长度，再向下平移4个单位长度 C．先向右平移1个单位长度，再向上平移5个单位长度 D．先向右平移2个单位长度，再向上平移4个单位长度2．（2020•菏泽）一次函数y＝acx+b与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（ B 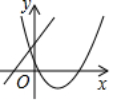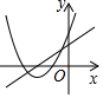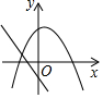）                                      B.                  C.                  D.3．（2020•温州）已知（﹣3，y1），（﹣2，y2），（1，y3）是抛物线y＝﹣3x2﹣12x+m上的点，则（ B ） A．y3＜y2＜y1    B．y3＜y1＜y2    C．y2＜y3＜y1      D．y1＜y3＜y24．（2020•西藏）当﹣1≤x≤3时，二次函数y＝x2﹣4x+5有最大值m，则m＝10　 ．【布置作业】 【教学反思】通过本节课的学习，培养了学生的归纳及概括问题的能力，还可使学生将知识进行梳理并培养系统化，起到提升能力，内化认知结构的作用。