


江苏省宜兴市环科园联盟2022-2023学年数学七下期末学业水平测试试题含答案
展开江苏省宜兴市环科园联盟2022-2023学年数学七下期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.某学校初、高六个年级共有![]() 名学生,为了了解其视力情况,现采用抽样调查,如果按
名学生,为了了解其视力情况,现采用抽样调查,如果按![]() 的比例抽样,则样本容量是( )
的比例抽样,则样本容量是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,被笑脸盖住的点的坐标可能是( )
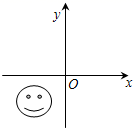
A.(3,2) B.(-3,2) C.(-3,-2) D.(3,-2)
3.若正比例函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.在下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
5.下列命题中正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
6.学校为了了解八年级学生参加课外活动兴趣小组的情况,随机抽查了40名学生(每人只能参加一个兴趣小组),将调查结果列出如下统计表,则八年级学生参加书法兴趣小组的频率是( )
组别 | 书法 | 绘画 | 舞蹈 | 其它 |
人数 | 8 | 12 | 11 | 9 |
A.0.1 B.0.15 C.0.2 D.0.3
7.设![]() 、
、![]() 是方程
是方程![]() 的两根,则
的两根,则![]() +
+![]() =( )
=( )
A.-3 B.-1 C.1 D.3
8.小明3分钟共投篮80次,进了50个球,则小明进球的频率是( ).
A.80 B.50 C.1.6 D.0.625
9.下列各式中,正确的是( )
A.![]() =﹣8 B.﹣
=﹣8 B.﹣![]() =﹣8 C.
=﹣8 C.![]() =±8 D.
=±8 D.![]() =±8
=±8
10.如图,有一个矩形纸片ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF的长为( )
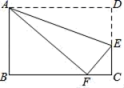
A.5 B.6 C.7 D.8
二、填空题(本大题共有6小题,每小题3分,共18分)
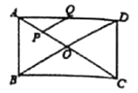
11.如图,矩形ABCD的对角线AC与BD相交点O,![]() ,P、Q分别为AO、AD的中点,则PQ的长度为________.
,P、Q分别为AO、AD的中点,则PQ的长度为________.
12.计算:![]() _______,化简
_______,化简![]() __________.
__________.
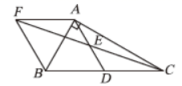
13.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 交
交![]() 的延长线于
的延长线于![]() ,则四边形
,则四边形![]() 的面积为______.
的面积为______.
14.一元二次方程![]() 的解为______.
的解为______.
15.如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
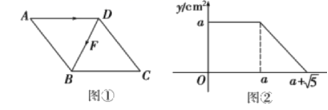
16.当a=______时,![]() 的值为零.
的值为零.
三、解下列各题(本大题共8小题,共72分)
17.(8分)(1)分解因式:![]()
(2)解不等式组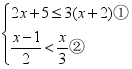
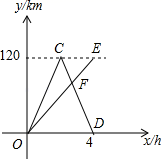
18.(8分)A、B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
(1)求甲车返回时(即CD段)![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(2)若当它们行驶了2.5h时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)直接写出当两车相距20km时,甲车行驶的时间.
19.(8分)某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数/人 | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
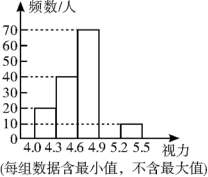
(1)在频数分布表中,a=_________,b=_________;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
20.(8分)已知关于x的方程x2-(m+2)x+(2m-1)=1.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
21.(8分)在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,
,![]() 的面积为1.
的面积为1.
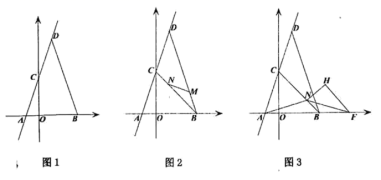
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,连接
上,连接![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,如图3,连接![]() ,点
,点![]() 为
为![]() 轴正半轴上点
轴正半轴上点![]() 右侧一点,点
右侧一点,点![]() 为第一象限内一点,
为第一象限内一点,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,直线
上一点,直线![]() 经过点
经过点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,请你判断四边形
,请你判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
22.(10分)如图,△ABC中,∠A=60°,∠C=40°,DE垂直平分BC,连接BD.
(1)尺规作图:过点D作AB的垂线,垂足为F.(保留作图痕迹,不写作法)
(2)求证:点D到BA,BC的距离相等.

23.(10分)某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
24.(12分)某公司对应聘者A,B进行面试,并按三个方面给应聘者打分,每方面满分20分,打分结果如下表:
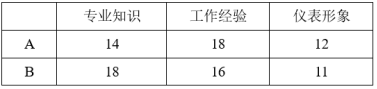
根据实际需要,公司将专业知识、工作经验和仪表形象三项成绩得分按6:1:3的比例确定两人的成绩,通过计算说明谁将被录用.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、D
4、C
5、C
6、C
7、B
8、D
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、![]()
![]()
13、12
14、![]()
15、![]()
16、﹣1.
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ;(2)
;(2)![]() .
.
18、(1)![]() (2)
(2)![]() (3)
(3)![]()
19、(1)60,0.2 (2)见解析(3)70%
20、(1)见详解;(2)4+![]() 或4+
或4+![]() .
.
21、(1)B(6,0);(2)d=![]() ;(3)四边形
;(3)四边形![]() 是矩形,理由见解析
是矩形,理由见解析
22、(1)如图所示,DF即为所求,见解析;(2)见解析.
23、(1)A型机器人每小时搬运150千克材料,B型机器人每小时搬运120千克材料;(2)至少购进A型机器人14台.
24、应聘者![]() 将被录用
将被录用
江苏省宜兴市宜城环科园教联盟2023-2024学年数学九上期末质量检测试题含答案: 这是一份江苏省宜兴市宜城环科园教联盟2023-2024学年数学九上期末质量检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
江苏省宜兴市环科园联盟2023-2024学年八上数学期末考试试题含答案: 这是一份江苏省宜兴市环科园联盟2023-2024学年八上数学期末考试试题含答案,共7页。试卷主要包含了式子的值不可能等于,下列命题是真命题的是,若是关于的完全平方式,则的值为等内容,欢迎下载使用。
江苏省宜兴市环科园联盟2023-2024学年八上数学期末质量检测试题含答案: 这是一份江苏省宜兴市环科园联盟2023-2024学年八上数学期末质量检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,在二次根式中,最简二次根式的有,方程组 的解是,下列命题中,是假命题的是等内容,欢迎下载使用。












