


江苏省苏州市虎丘区立达中学2022-2023学年七年级数学第二学期期末检测模拟试题含答案
展开
这是一份江苏省苏州市虎丘区立达中学2022-2023学年七年级数学第二学期期末检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
江苏省苏州市虎丘区立达中学2022-2023学年七年级数学第二学期期末检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题(每小题3分,共30分)1.在□ABCD中,对角线 AC与 BD 相交于点O , AC10, BD 6,则下列线段不可能是□ABCD 的边长的是( )A.5 B.6 C.7 D.82.如图,在四边形ABCD中,AB=BC=2,且∠B=∠D=90°,连接AC,那么四边形ABCD的最大面积是( )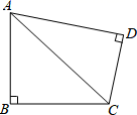 A.2
A.2![]() B.4 C.4
B.4 C.4![]() D.83.下列说法中,正确的是( )A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线相等的四边形是矩形C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形4.已知a、b、c是
D.83.下列说法中,正确的是( )A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线相等的四边形是矩形C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形4.已知a、b、c是![]() 的三边,且满足
的三边,且满足![]() ,则
,则![]() 一定是( )A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形5.如图,在
一定是( )A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形5.如图,在![]() 中,
中,![]() 平分
平分![]() ,且
,且![]() ,则
,则![]() 的周长为( )
的周长为( )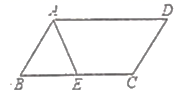 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
6.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )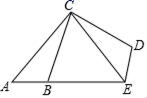 A.1.5 B.3 C.4 D.57.如图,等腰三角形
A.1.5 B.3 C.4 D.57.如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() , 腰
, 腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于
边于![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段EF上一动点,则
为线段EF上一动点,则![]() 周长的最小值为( )
周长的最小值为( )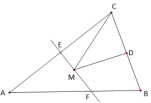 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.在求3x的倒数的值时,嘉淇同学误将3x看成了8x,她求得的值比正确答案小5.依上述情形,所列关系式成立的是( )A.
8.在求3x的倒数的值时,嘉淇同学误将3x看成了8x,她求得的值比正确答案小5.依上述情形,所列关系式成立的是( )A.![]() =
=![]() -5 B.
-5 B.![]() =
=![]() +5 C.
+5 C.![]() =8x-5 D.
=8x-5 D.![]() =8x+59.某单位组织职工开展植树活动,植树量与人数之间的关系如下表,下列说法不正确的是()植树量(棵)34567人数410861A.参加本次植树活动共有29人 B.每人植树量的众数是4C.每人植树量的中位数是5 D.每人植树量的平均数是510.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
=8x+59.某单位组织职工开展植树活动,植树量与人数之间的关系如下表,下列说法不正确的是()植树量(棵)34567人数410861A.参加本次植树活动共有29人 B.每人植树量的众数是4C.每人植树量的中位数是5 D.每人植树量的平均数是510.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )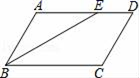 A.150° B.130° C.120° D.100°二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向160米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为________米.
A.150° B.130° C.120° D.100°二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向160米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为________米. 12.如图是某超市一层到二层电梯的示意图,其中AB、CD分别表示超市一层、二层电梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘电梯从点B到点C上升的高度h约为________米.
12.如图是某超市一层到二层电梯的示意图,其中AB、CD分别表示超市一层、二层电梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘电梯从点B到点C上升的高度h约为________米.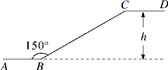 13.张老师对同学们的打字能力进行测试,他将全班同学分成五组.经统计,这五个小组平均每分钟打字个数如下:100,80,x,90,90,已知这组数据的众数与平均数相等,那么这组数据的中位数是 .14.关于x的一次函数
13.张老师对同学们的打字能力进行测试,他将全班同学分成五组.经统计,这五个小组平均每分钟打字个数如下:100,80,x,90,90,已知这组数据的众数与平均数相等,那么这组数据的中位数是 .14.关于x的一次函数![]() ,当
,当![]() _________时,它的图象过原点.15.分解因式:
_________时,它的图象过原点.15.分解因式:![]() 16.函数y=kx(k
16.函数y=kx(k![]() 0)的图象上有两个点A1(
0)的图象上有两个点A1(![]() ,
,![]() ),A2(
),A2(![]() ,
,![]() ),当
),当![]() <
<![]() 时,
时,![]() >
>![]() ,写出一个满足条件的函数解析式______________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,已知一次函数y=﹣
,写出一个满足条件的函数解析式______________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,已知一次函数y=﹣![]() x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=
x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,ND=
ON,ND=![]() NP.(1)b= ;(2)求证:四边形BCDE是平行四边形;(3)在直线y=﹣
NP.(1)b= ;(2)求证:四边形BCDE是平行四边形;(3)在直线y=﹣![]() x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.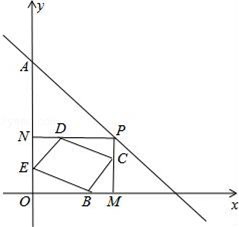 18.(8分)某移动通信公司推出了如下两种移动电话计费方式, 月使用费/元主叫限定时间/分钟主叫超时费(元/分钟)方式一306000.20方式二506000.25说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)(1)请根据题意完成如表的填空; 月主叫时间500分钟月主叫时间800分钟方式一收费/元 130方式二收费/元50 (2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;(3)请计算说明选择哪种计费方式更省钱. 19.(8分)对于平面直角坐标系xOy中的点P和正方形给出如下定义:若正方形的对角线交于点O,四条边分别和坐标轴平行,我们称该正方形为原点正方形,当原点正方形上存在点Q,满足PQ≤1时,称点P为原点正方形的友好点.(1)当原点正方形边长为4时,①在点P1(0,0),P2(-1,1),P3(3,2)中,原点正方形的友好点是__________;②点P在直线y=x的图象上,若点P为原点正方形的友好点,求点P横坐标的取值范围;(2)乙次函数y=-x+2的图象分别与x轴,y轴交于点A,B,若线段AB上存在原点正方形的友好点,直接写出原点正方形边长a的取值范围.
18.(8分)某移动通信公司推出了如下两种移动电话计费方式, 月使用费/元主叫限定时间/分钟主叫超时费(元/分钟)方式一306000.20方式二506000.25说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)(1)请根据题意完成如表的填空; 月主叫时间500分钟月主叫时间800分钟方式一收费/元 130方式二收费/元50 (2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;(3)请计算说明选择哪种计费方式更省钱. 19.(8分)对于平面直角坐标系xOy中的点P和正方形给出如下定义:若正方形的对角线交于点O,四条边分别和坐标轴平行,我们称该正方形为原点正方形,当原点正方形上存在点Q,满足PQ≤1时,称点P为原点正方形的友好点.(1)当原点正方形边长为4时,①在点P1(0,0),P2(-1,1),P3(3,2)中,原点正方形的友好点是__________;②点P在直线y=x的图象上,若点P为原点正方形的友好点,求点P横坐标的取值范围;(2)乙次函数y=-x+2的图象分别与x轴,y轴交于点A,B,若线段AB上存在原点正方形的友好点,直接写出原点正方形边长a的取值范围. 20.(8分)如图,四边形
20.(8分)如图,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于
于![]() .
.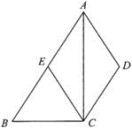 (1)求证:四边形
(1)求证:四边形![]() 是菱形;(2)若点
是菱形;(2)若点![]() 是
是![]() 的中点,试判断
的中点,试判断![]() 的形状,并说明理由. 21.(8分)如图,平行四边形
的形状,并说明理由. 21.(8分)如图,平行四边形![]() 中,点
中,点![]() 分别是
分别是![]() 的中点.求证
的中点.求证![]() .
.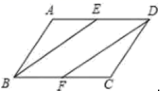 22.(10分)小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym.图中的折线表示小亮在整个行走过程中y与x的函数关系.
22.(10分)小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym.图中的折线表示小亮在整个行走过程中y与x的函数关系.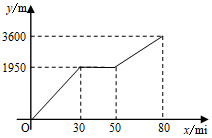 (1)小亮行走的总路程是______m,他途中休息了______min,休息后继续行走的速度为______m/min;(2)当
(1)小亮行走的总路程是______m,他途中休息了______min,休息后继续行走的速度为______m/min;(2)当![]() 时,求y与x的函数关系式;(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少? 23.(10分)因式分解:(1)
时,求y与x的函数关系式;(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少? 23.(10分)因式分解:(1)![]() ; (2)
; (2)![]() . 24.(12分)如图,在
. 24.(12分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的高,过点
边上的高,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .
.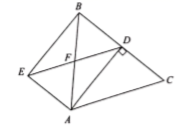 (1)求证:四边形
(1)求证:四边形![]() 是矩形;(2)求四边形
是矩形;(2)求四边形![]() 的周长. 参考答案 一、选择题(每小题3分,共30分)1、D2、B3、C4、C5、D6、A7、C8、B9、D10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、113、1.14、
的周长. 参考答案 一、选择题(每小题3分,共30分)1、D2、B3、C4、C5、D6、A7、C8、B9、D10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、113、1.14、![]() 15、
15、![]() 16、y=-x(k<0即可) 三、解下列各题(本大题共8小题,共72分)17、(1)1;(2)证明见解析;(1)在直线y=﹣
16、y=-x(k<0即可) 三、解下列各题(本大题共8小题,共72分)17、(1)1;(2)证明见解析;(1)在直线y=﹣![]() x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).18、(1)70;100;(2)详见解析;(3)当0≤t≤400时方式一省钱;当400<t≤1400时,方式二省钱,当t>1400时,方式一省钱,当为400分钟、1400分钟时,两种方式费用相同.19、(1)①P2,P3 ,②1≤x≤
x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).18、(1)70;100;(2)详见解析;(3)当0≤t≤400时方式一省钱;当400<t≤1400时,方式二省钱,当t>1400时,方式一省钱,当为400分钟、1400分钟时,两种方式费用相同.19、(1)①P2,P3 ,②1≤x≤![]() 或
或![]() ≤x≤-1;(2)2-
≤x≤-1;(2)2-![]() ≤a≤1.20、(1)详见解析;(2)
≤a≤1.20、(1)详见解析;(2)![]() 是直角三角形,理由详见解析.21、见解析22、(1)3600,20,1;(2)y=1x-2;(3)当小颖到达缆车终点时,小亮离缆车终点的路程是1100m.23、 (1) (a-1)(a+1);(1) 3(x-y)1.24、(1)见详解;(2)
是直角三角形,理由详见解析.21、见解析22、(1)3600,20,1;(2)y=1x-2;(3)当小颖到达缆车终点时,小亮离缆车终点的路程是1100m.23、 (1) (a-1)(a+1);(1) 3(x-y)1.24、(1)见详解;(2)![]()
相关试卷
这是一份72,江苏省苏州市姑苏区立达中学校2023-2024学年七年级上学期期末数学试题,共22页。试卷主要包含了 相反数是, 下面的计算正确的是, 单项式的次数是____.等内容,欢迎下载使用。
这是一份江苏省苏州市虎丘区立达中学2023-2024学年九上数学期末检测模拟试题含答案,共7页。试卷主要包含了如图,该几何体的主视图是,已知,则等于,对于二次函数,下列说法正确的是等内容,欢迎下载使用。
这是一份2023-2024学年江苏省苏州市虎丘区立达中学数学八上期末教学质量检测试题含答案,共7页。试卷主要包含了命题“邻补角的和为”的条件是等内容,欢迎下载使用。









