


河南省信阳九中学2022-2023学年七年级数学第二学期期末经典模拟试题含答案
展开
这是一份河南省信阳九中学2022-2023学年七年级数学第二学期期末经典模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,已知,则的值是,如图等内容,欢迎下载使用。
河南省信阳九中学2022-2023学年七年级数学第二学期期末经典模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.某楼盘2016年房价为每平方米15600元,经过两年连续降价后,2018年房价为每平方米12400元。设该楼盘这两年房价每年平均降低率为x,根据题意可列方程为( )A.15600(1-2x)=12400 B.2×15600(1-2x)=12400C.15600(1-x)2=12400 D.15600(1-x2)=124002.如图,把![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )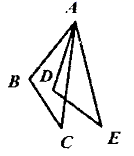 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.在Rt△ABC中,斜边长AB=3,AB²+AC²+BC²的值为( )A.18 B.24 C.15 D.无法计算4.正三角形、正方形、等腰直角三角形、平行四边形中,既是轴对称图形又是中心对称图形的是( )A.正三角形 B.正方形 C.等腰直角三角形 D.平行四边形5.下列函数解析式中不是一次函数的是( )A.
3.在Rt△ABC中,斜边长AB=3,AB²+AC²+BC²的值为( )A.18 B.24 C.15 D.无法计算4.正三角形、正方形、等腰直角三角形、平行四边形中,既是轴对称图形又是中心对称图形的是( )A.正三角形 B.正方形 C.等腰直角三角形 D.平行四边形5.下列函数解析式中不是一次函数的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.如图,在▱ABCD中,对角线AC、BD相交于点O,下列哪个条件不能判定▱ABCD是矩形的是( )
6.如图,在▱ABCD中,对角线AC、BD相交于点O,下列哪个条件不能判定▱ABCD是矩形的是( )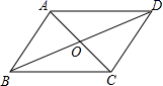 A.AC=BD B.OA=OB C.∠ABC=90° D.AB=AD7.已知
A.AC=BD B.OA=OB C.∠ABC=90° D.AB=AD7.已知![]() ,则
,则![]() 的值是( )A.
的值是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.如图:
8.如图:![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )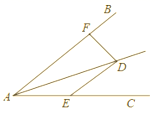 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数
9.如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )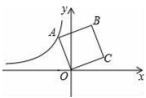 A.﹣2 B.﹣4 C.﹣
A.﹣2 B.﹣4 C.﹣![]() D.
D.![]() 10.一次函数
10.一次函数![]() 在平面直角坐标系内的图像如图所示,则k和b的取值范围是( )
在平面直角坐标系内的图像如图所示,则k和b的取值范围是( )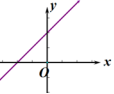 A.
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,小丽在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域离网3米的位置上,已知她的击球高度是2.4米,则她应站在离网________米处.
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,小丽在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域离网3米的位置上,已知她的击球高度是2.4米,则她应站在离网________米处.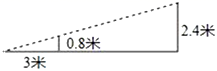 12.在一个不透明的袋子中有若千个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:摸球实验次数100100050001000050000100000“摸出黑球”的次数36387201940091997040008“摸出黑球”的频率(结果保留小数点后三位)0.3600.3870.4040.4010.3990.400根据试验所得数据,估计“摸出黑球”的概率是_______(结果保留小数点后一位).13.如图,
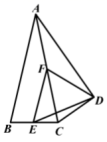
12.在一个不透明的袋子中有若千个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:摸球实验次数100100050001000050000100000“摸出黑球”的次数36387201940091997040008“摸出黑球”的频率(结果保留小数点后三位)0.3600.3870.4040.4010.3990.400根据试验所得数据,估计“摸出黑球”的概率是_______(结果保留小数点后一位).13.如图,![]() 中,
中,![]() ,以
,以![]() 为斜边作
为斜边作![]() ,使
,使![]()
![]()
![]() 分别是
分别是![]() 的中点,则
的中点,则![]() __________.
__________. 14.如果正数m的平方根为x+1和x-3,则m的值是_____15.直线y=﹣3x+5与x轴交点的坐标是_____.16.169的算术平方根是______.三、解下列各题(本大题共8小题,共72分)17.(8分)某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.
14.如果正数m的平方根为x+1和x-3,则m的值是_____15.直线y=﹣3x+5与x轴交点的坐标是_____.16.169的算术平方根是______.三、解下列各题(本大题共8小题,共72分)17.(8分)某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.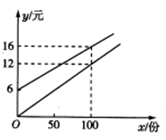 (1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算. 18.(8分)感知:如图①,在正方形
(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算. 18.(8分)感知:如图①,在正方形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连结
重合),连结![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .易知
.易知![]() ,进而证出
,进而证出![]() .探究:如图②,点
.探究:如图②,点![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连结
重合),连结![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .应用:如图②,若
.应用:如图②,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________.
的面积为________.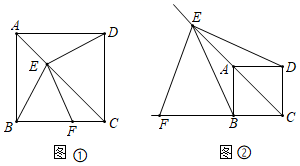 19.(8分)如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,
19.(8分)如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,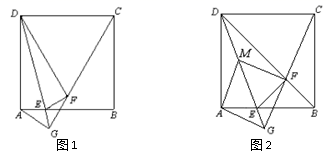 (1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。 20.(8分)古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
(1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。 20.(8分)古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.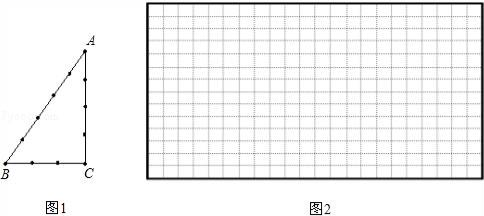 (1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数 (3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.) 21.(8分)为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.(1)请将条形统计图补充完整;(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数 (3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.) 21.(8分)为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.(1)请将条形统计图补充完整;(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?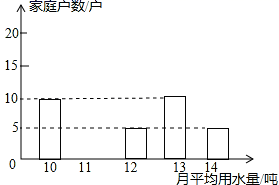 22.(10分)在平面直角坐标系xOy中,对于两点A,B,给出如下定义:以线段AB为边的正方形称为点A,B的“确定正方形”.如图为点A,B 的“确定正方形”的示意图.
22.(10分)在平面直角坐标系xOy中,对于两点A,B,给出如下定义:以线段AB为边的正方形称为点A,B的“确定正方形”.如图为点A,B 的“确定正方形”的示意图.
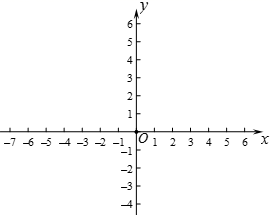 (1)如果点M的坐标为(0,1),点N的坐标为(3,1),那么点M,N的“确定正方形”的面积为___________;(2)已知点O的坐标为(0,0),点C为直线
(1)如果点M的坐标为(0,1),点N的坐标为(3,1),那么点M,N的“确定正方形”的面积为___________;(2)已知点O的坐标为(0,0),点C为直线![]() 上一动点,当点O,C的“确定正方形”的面积最小,且最小面积为2时,求b的值.(3)已知点E在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为P(m,0),点F在直线
上一动点,当点O,C的“确定正方形”的面积最小,且最小面积为2时,求b的值.(3)已知点E在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为P(m,0),点F在直线![]() 上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围. 23.(10分)如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN是平行四边形;(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。
上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围. 23.(10分)如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN是平行四边形;(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。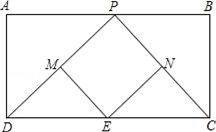 24.(12分)如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距_____千米;(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时;(3)B出发后_____小时与A相遇;(4)求出A行走的路程S与时间t的函数关系式;(写出计算过程)(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇.
24.(12分)如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距_____千米;(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时;(3)B出发后_____小时与A相遇;(4)求出A行走的路程S与时间t的函数关系式;(写出计算过程)(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇.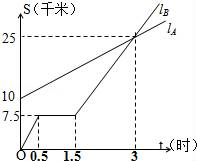 参考答案 一、选择题(每小题3分,共30分)1、C2、D3、A4、B5、C6、D7、D8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、612、0.113、
参考答案 一、选择题(每小题3分,共30分)1、C2、D3、A4、B5、C6、D7、D8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、612、0.113、![]() 14、415、 (
14、415、 (![]() ,
,![]() )16、1 三、解下列各题(本大题共8小题,共72分)17、(3)y=3.33x+6;y=3.33x(3)当333≤x<333时,选择乙种印刷方式较合算;当x=333时,选择甲、乙两种印刷方式都可以;当333<x≤453时,选择甲种印刷方式较合算.18、探究:见解析;应用:
)16、1 三、解下列各题(本大题共8小题,共72分)17、(3)y=3.33x+6;y=3.33x(3)当333≤x<333时,选择乙种印刷方式较合算;当x=333时,选择甲、乙两种印刷方式都可以;当333<x≤453时,选择甲种印刷方式较合算.18、探究:见解析;应用:![]() 19、 (1) ∠DGC=45°; (2) ∠DGC=45°不会变化; (3) 四边形AGFM是正方形20、(1)B(2)(6,8,10)(3)见解析21、 (1)补图见解析;(2)11.6,11,11;()210户.22、(1)9;(2)OC⊥直线
19、 (1) ∠DGC=45°; (2) ∠DGC=45°不会变化; (3) 四边形AGFM是正方形20、(1)B(2)(6,8,10)(3)见解析21、 (1)补图见解析;(2)11.6,11,11;()210户.22、(1)9;(2)OC⊥直线![]() 于点C;①
于点C;① ![]() ;②
;② ![]() ;(3)
;(3)![]() 23、(1)证明见解析;(2)当PA=5时,四边形PMEN为菱形,理由见解析.24、(1)10;(2)1;(3)3;(4)
23、(1)证明见解析;(2)当PA=5时,四边形PMEN为菱形,理由见解析.24、(1)10;(2)1;(3)3;(4)![]() ;(5)1小时.
;(5)1小时.
相关试卷
这是一份2023-2024学年河南省信阳市第九中学数学九上期末经典试题含答案,共8页。试卷主要包含了已知二次函数y=x2﹣6x+m等内容,欢迎下载使用。
这是一份河南省信阳九中学2023-2024学年数学八上期末调研模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,①实数和数轴上的点一一对应等内容,欢迎下载使用。
这是一份河南省信阳市浉河区第九中学2022-2023学年数学七年级第二学期期末统考模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,点P,下列式子是分式的是等内容,欢迎下载使用。









