洛阳市重点中学2022-2023学年数学七年级第二学期期末教学质量检测模拟试题含答案

洛阳市重点中学2022-2023学年数学七年级第二学期期末教学质量检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知4＜m＜5，则关于x的不等式组的整数解共有（　　）

A．1个 B．2个 C．3个 D．4个

2．下列命题的逆命题成立的是（　　）

A．对顶角相等 B．两直线平行，同位角相等

C．如果a＝b，那么a2 ＝b2 D．正方形的四条边相等

3．如图，在菱形ABCD中，对角线AC与BD相交于点O，若BC＝3，∠ABC＝60°，则BD的长为（　　）

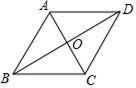
A．2 B．3 C． D．

4．设直角三角形的两条直角边分别为a和b，斜边长为c，已知，，则（    ）

A．3 B．4 C．5 D．8

5．若四边形的两条对角线相等，则顺次连接该四边形各边中点所得的四边形是(    )

A．梯形 B．矩形 C．菱形 D．正方形

6．某校为了了解学生在校午餐所需的时间，抽查了 20 名同学在校午餐所需的时间，获得如 下数据（单位：分）：10，12，15，10，1，18，19，18，20，34，22，25，20，18，18，20，15，1，21，1．若将这些数据分为 5组，则组距是（    ）

A．4 分 B．5 分 C．6 分 D．7 分

7．化简的结果是（    ）

A．2 B．-4 C．4 D．±4

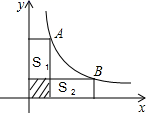
8．如图，A、B是曲线上的点，经过A、B两点向x轴、y轴作垂线段，若，则S1+S2的值为（　　）

A．3 B．4 C．5 D．6

9．从﹣4，﹣3，﹣2，﹣1，0，1，3，4，5这九个数中，随机抽取一个数，记为a，则数a使关于x的不等式组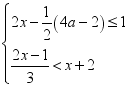至少有四个整数解，且关于x的分式方程＝1有非负整数解的概率是（　　）

A． B． C． D．

10．如图，在平行四边形ABCD中，AC与BD相交于O，且AO=BD=4，AD=3，则△BOC的周长为（　　）

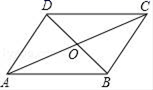
A．9 B．10 C．12 D．14

11．已知,下列不等式中错误的是（   ）

A． B． C． D．

12．已知点A的坐标为（3，﹣6），则点A所在的象限是（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

二、填空题（每题4分，满分20分，将答案填在答题纸上）

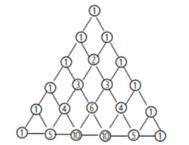
13．我国古代数学领域有些研究成果曾位居世界前列，其中“杨辉三角”就是一例．南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中，用图中的三角形解释二项和的乘方规律．杨辉三角两腰上的数都是1，其余每个数都为它的上方(左右)两数之和，这个三角形给出了(a+b)n(n=1，2，3，4，5)的展开式(按a的次数由大到小的顺序)的系数规律．例如，此三角形中第3行的3个数1，2，1，恰好对应着(a+b)2=a2+2ab+b2展开式中各项的系数：第4行的4个数1，3，3，1，恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中各项的系数，等等．利用上面呈现的规律填空：(a+b)6=a6+6a5b+________ +20a3b3+15a2b4+ ________+b6

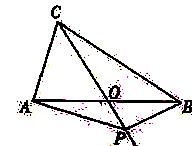
14．如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为       ．

15．如图，直线y=-x+4分别与x轴，y轴交于点A，B，点C在直线AB上，D是y轴右侧平面内一点，若以点O，A，C，D为顶点的四边形是菱形，则点D的坐标是_______________．

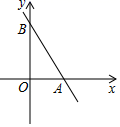
16． “暑期乒乓球夏令营”开始在学校报名了，已知甲、乙、丙三个夏令营组人数相等，且每组学生的平均年龄都是14岁，三个组学生年龄的方差分别是，， 如果今年暑假你也准备报名参加夏令营活动，但喜欢和年龄相近的同伴相处，那么你应选择是________.

17．等边三角形的边长是4，则高AD_________ （结果精确到0.1）

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，在矩形ABCD中，AB＝8，AD＝6，将矩形ABCD绕点A逆时针旋转得到矩形AEFG．

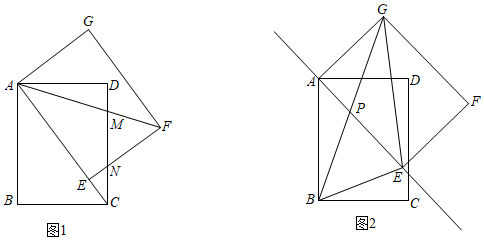
（1）如图1，若在旋转过程中，点E落在对角线AC上，AF，EF分别交DC于点M，N．

①求证：MA＝MC；

②求MN的长；

（2）如图2，在旋转过程中，若直线AE经过线段BG的中点P，连接BE，GE，求△BEG的面积

19．（5分）第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行．为了调查学生对冬奥知识的了解情况，从甲、乙两校各随机抽取20名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．

a．甲校20名学生成绩的频数分布表和频数分布直方图如下：

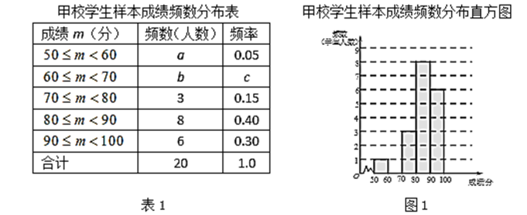
b．甲校成绩在的这一组的具体成绩是：

87   88   88   88   89   89   89   89   

c．甲、乙两校成绩的平均分、中位数、众数、方差如下：

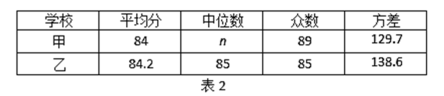
根据以上图表提供的信息，解答下列问题：

（1）表1中a =　　          ；表2中的中位数n =　　          ；

（2）补全图1甲校学生样本成绩频数分布直方图；

（3）在此次测试中，某学生的成绩是87分，在他所属学校排在前10名，由表中数据可知该学生是     校的学生（填“甲”或“乙”），理由是                          ；

（4）假设甲校200名学生都参加此次测试，若成绩80分及以上为优秀，估计成绩优秀的学生人数为__________．

20．（8分）健身运动已成为时尚，某公司计划组装A、B两种型号的健身器材共40套，捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个，组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个，乙种部件196个.

（1）公司在组装A、B两种型号的健身器材时，共有多少种组装方案？

（2）组装一套A型健身器材需费用20元，组装一套B型健身器材需费用18元，求总组装费用最少的组装方案，最少总组装费用是多少？

21．（10分）解不等式组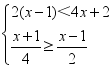：，并在数轴上表示出它的解集．

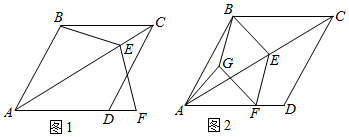
22．（10分）如图，在菱形ABCD中，∠ABC＝120°，AB＝4，E为对角线AC上的动点（点E不与A，C重合），连接BE，将射线EB绕点E逆时针旋转120°后交射线AD于点F．

（1）如图1，当AE＝AF时，求∠AEB的度数；

（2）如图2，分别过点B，F作EF，BE的平行线，且两直线相交于点G．

①试探究四边形BGFE的形状，并求出四边形BGFE的周长的最小值；

②连接AG，设CE＝x，AG＝y，请直接写出y与x之间满足的关系式，不必写出求解过程．

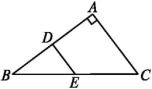
23．（12分）如图，在Rt△ABC中，∠A=90°，∠B=30°，D、E分别是AB、BC的中点，若DE=3，求BC的长.

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、B

3、C

4、B

5、C

6、B

7、C

8、B

9、C

10、A

11、D

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、15a4b2    6ab5   

14、1或1或1

15、（2，−2）或（6，2）．

16、乙组

17、3.1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）①见解析；②；（2）△BEG的面积为48﹣6或48+6

19、（1）1，88.5；（2）见解析；（3）乙，乙的中位数是85，87>85；（4）140

20、（1）组装A、B两种型号的健身器材共有9种组装方案；（2）总组装费用最少的组装方案：组装A型器材22套，组装B型器材18套

21、﹣2＜x≤3

22、（1）45°；（2）①四边形BEFG是菱形，8；② y＝（0＜x＜12）

23、12.