


浙江省嘉兴、舟山2022-2023学年数学七下期末检测试题含答案
展开
这是一份浙江省嘉兴、舟山2022-2023学年数学七下期末检测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,已知点A的坐标为,在平面直角坐标系中,点M,一束光线从点A,下列等式成立的是等内容,欢迎下载使用。
浙江省嘉兴、舟山2022-2023学年数学七下期末检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各组数据中能作为直角三角形的三边长的是( )A.1,2,2 B.![]() C.13,14,15 D.6,8,102.下列多项式中,可以使用平方差公式进行因式分解的是( )A.x
C.13,14,15 D.6,8,102.下列多项式中,可以使用平方差公式进行因式分解的是( )A.x![]() +1 B.﹣x
+1 B.﹣x![]() +1 C.x
+1 C.x![]() +x D.x
+x D.x![]() +2x+13.四边形的内角和为( )A.180° B.360° C.540° D.720°4.如图 ,△ABC 中,∠B=90°,AD 是∠BAC 的平分线,DE⊥AC,垂足为 E,则下列结论中不正确的是( )
+2x+13.四边形的内角和为( )A.180° B.360° C.540° D.720°4.如图 ,△ABC 中,∠B=90°,AD 是∠BAC 的平分线,DE⊥AC,垂足为 E,则下列结论中不正确的是( )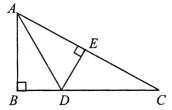 A.AB=AE B.BD=DE C.∠ADE=∠CDE D.∠ADB=∠ADE5.已知点A的坐标为(3,﹣6),则点A所在的象限是( )A.第一象限 B.第二象限 C.第三象限 D.第四象限6.在平面直角坐标系中,点M(2019,–2019)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限7.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )A.4 B.5 C.6 D.78.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A.AB=AE B.BD=DE C.∠ADE=∠CDE D.∠ADB=∠ADE5.已知点A的坐标为(3,﹣6),则点A所在的象限是( )A.第一象限 B.第二象限 C.第三象限 D.第四象限6.在平面直角坐标系中,点M(2019,–2019)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限7.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )A.4 B.5 C.6 D.78.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )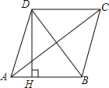 A.
A.![]() B.
B.![]() C.5 D.49.如果在一组数据中,23、25、28、22出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的众数和中位数分别是( )A.24、25 B.25、24 C.25、25 D.23、2510.下列等式成立的是( )A.
C.5 D.49.如果在一组数据中,23、25、28、22出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的众数和中位数分别是( )A.24、25 B.25、24 C.25、25 D.23、2510.下列等式成立的是( )A.![]() •
•![]() =
=![]() B.
B.![]() =2
=2![]() C.
C.![]() ﹣
﹣![]() =
=![]() D.
D.![]() =﹣311.一次函数
=﹣311.一次函数![]() 的图象经过点
的图象经过点![]() ,且
,且![]() 的值随
的值随![]() 的增大而增大,则点
的增大而增大,则点![]() 的坐标可以为( )A.
的坐标可以为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.下列图形中,可以看作是中心对称图形的是( )A.
12.下列图形中,可以看作是中心对称图形的是( )A. B.
B. C.
C. D.
D. 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,菱形
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,菱形![]() 的对角线交于点
的对角线交于点![]() 为
为![]() 边的中点,如果菱形的周长为
边的中点,如果菱形的周长为![]() ,那么
,那么![]() 的长是__________.
的长是__________.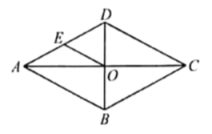 14.当
14.当![]() _____时,分式
_____时,分式![]() 的值为1.15.直线
的值为1.15.直线![]() 过第_________象限,且
过第_________象限,且![]() 随
随![]() 的增大而_________.16.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为_____m.
的增大而_________.16.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为_____m.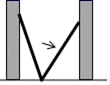 17.已知
17.已知![]() ,则
,则![]() __________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)在校园手工制作活动中,现有甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同,求乙每小时制作多少朵纸花? 19.(5分)先阅读下面的内容,再解决问题:问题:对于形如
__________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)在校园手工制作活动中,现有甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同,求乙每小时制作多少朵纸花? 19.(5分)先阅读下面的内容,再解决问题:问题:对于形如![]() 这样的二次三项式,可以用公式法将它分解成
这样的二次三项式,可以用公式法将它分解成![]() 的形式. 但对于二次三项式
的形式. 但对于二次三项式![]() ,就不能直接运用公式了. 此时,我们可以在二次三项式
,就不能直接运用公式了. 此时,我们可以在二次三项式![]() 中先加上一项
中先加上一项![]() ,使它与
,使它与![]() 成为一个完全平方式,再减去
成为一个完全平方式,再减去![]() ,整个式子的值不变,于是有:
,整个式子的值不变,于是有:![]()
![]()
![]()
![]()
![]() 像这样,先添一适当项,使式中出现完全平方式,再减去这项,使整个式子的值不变的方法称为“配方法”. 利用“配方法”,解决下列问题:(1)分解因式:
像这样,先添一适当项,使式中出现完全平方式,再减去这项,使整个式子的值不变的方法称为“配方法”. 利用“配方法”,解决下列问题:(1)分解因式:![]() ______;(2)若△ABC的三边长是a,b,c,且满足
______;(2)若△ABC的三边长是a,b,c,且满足![]() ,c边的长为奇数,求△ABC的周长的最小值;(3)当x为何值时,多项式
,c边的长为奇数,求△ABC的周长的最小值;(3)当x为何值时,多项式![]() 有最大值?并求出这个最大值. 20.(8分)如图,已知
有最大值?并求出这个最大值. 20.(8分)如图,已知![]() 分别是△
分别是△![]() 的边
的边![]() 上的点,若
上的点,若![]() ,
,![]() ,
,![]() .
.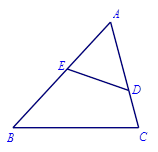 (1)请说明:△
(1)请说明:△![]() ∽△
∽△![]() ;(2)若
;(2)若![]() ,求
,求![]() 的长. 21.(10分)已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在AC上,且AE=CF,AH=CG.求证:四边形EGFH是平行四边形.
的长. 21.(10分)已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在AC上,且AE=CF,AH=CG.求证:四边形EGFH是平行四边形.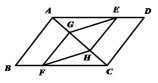 22.(10分)如图,AD 是△ABC 的角平分线,M 是 BC 的中点, FM∥AD 交 BA 的延长线于点 F,交 AC 于点 E.求证:
22.(10分)如图,AD 是△ABC 的角平分线,M 是 BC 的中点, FM∥AD 交 BA 的延长线于点 F,交 AC 于点 E.求证: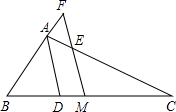 (1)CE=BF.(2)AB+AC=2CE. 23.(12分)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325 8430 8215 7453 7446 6754 7638 6834 7326 6830 8648 8753 9450 9865 7290 7850 对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:步数分组统计表 组别步数分组频数A5500≤x<65002B6500≤x<750010C7500≤x<8500mD8500≤x<95003E9500≤x<10500n
(1)CE=BF.(2)AB+AC=2CE. 23.(12分)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325 8430 8215 7453 7446 6754 7638 6834 7326 6830 8648 8753 9450 9865 7290 7850 对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:步数分组统计表 组别步数分组频数A5500≤x<65002B6500≤x<750010C7500≤x<8500mD8500≤x<95003E9500≤x<10500n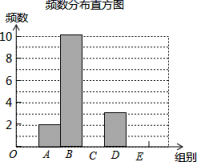 请根据以上信息解答下列问题:(1)填空:m= ______ ,n= ______ ;(2)补全频数发布直方图;(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、B3、B4、C5、D6、D7、B8、A9、C10、B11、C12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
请根据以上信息解答下列问题:(1)填空:m= ______ ,n= ______ ;(2)补全频数发布直方图;(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、B3、B4、C5、D6、D7、B8、A9、C10、B11、C12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、
14、![]() .15、16、2.217、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、乙每小时制作80朵纸花.19、(1)(a−3)(a−1);(2)当a=7,b=4,c=1时,△ABC的周长最小,最小值是:7+4+1=16;(3)当x=−1时,多项式−2x2−4x+3有最大值,最大值是1.20、(1)证明见解析(2)1221、见解析22、(1)见解析;(2)见解析23、(1)4;1;(2)见解析;(3)B;(4)48.
.15、16、2.217、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、乙每小时制作80朵纸花.19、(1)(a−3)(a−1);(2)当a=7,b=4,c=1时,△ABC的周长最小,最小值是:7+4+1=16;(3)当x=−1时,多项式−2x2−4x+3有最大值,最大值是1.20、(1)证明见解析(2)1221、见解析22、(1)见解析;(2)见解析23、(1)4;1;(2)见解析;(3)B;(4)48.
相关试卷
这是一份2023-2024学年浙江省嘉兴、舟山八上数学期末调研模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,如图,用,直接判定的理由是,下列各式从左到右变形正确的是等内容,欢迎下载使用。
这是一份浙江省嘉兴市秀洲片区2022-2023学年七下数学期末检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列命题中,不正确的是,已知数据等内容,欢迎下载使用。
这是一份浙江省嘉兴市海宁市许巷2022-2023学年七下数学期末教学质量检测模拟试题含答案,共6页。试卷主要包含了不等式3≥x+4的解集是,以下四个命题正确的是,分式的最简公分母是等内容,欢迎下载使用。








