


浙江省慈溪市(区域联考)2022-2023学年七年级数学第二学期期末监测试题含答案
展开
这是一份浙江省慈溪市(区域联考)2022-2023学年七年级数学第二学期期末监测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,﹣2018的倒数是,下列四组线段中,已知等内容,欢迎下载使用。
浙江省慈溪市(区域联考)2022-2023学年七年级数学第二学期期末监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.分式方程![]() -1=
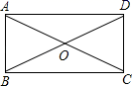
-1=![]() 的解为( )A.x=1 B.x=-1 C.无解 D.x=-22.如图, 矩形
的解为( )A.x=1 B.x=-1 C.无解 D.x=-22.如图, 矩形![]() 的对角线
的对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为
的长为![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.多项式m2﹣4与多项式m2﹣4m+4的公因式是( )A.m﹣2 B.m+2 C.m+4 D.m﹣44.在直角三角形中,若勾为3,股为4,则弦为( )A.5 B.6 C.7 D.85.已知函数
3.多项式m2﹣4与多项式m2﹣4m+4的公因式是( )A.m﹣2 B.m+2 C.m+4 D.m﹣44.在直角三角形中,若勾为3,股为4,则弦为( )A.5 B.6 C.7 D.85.已知函数![]() ,不在该函数图象上的点是( )A.
,不在该函数图象上的点是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
6.如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )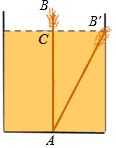 A.15尺 B.16尺 C.17尺 D.18尺7.﹣2018的倒数是( )A.2018 B.
A.15尺 B.16尺 C.17尺 D.18尺7.﹣2018的倒数是( )A.2018 B.![]() C.﹣2018 D.
C.﹣2018 D.![]() 8.下列四组线段中。可以构成直角三角形的是( )A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,3,39.已知:
8.下列四组线段中。可以构成直角三角形的是( )A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,3,39.已知:![]() ,计算:
,计算:![]() 的结果是()A.
的结果是()A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.关于函数y= -x-3的图象,有如下说法:①图象过点(0,-3);②图象与x轴的交点是(-3,0);③由图象可知y随x的增大而增大; ④图象不经过第一象限;⑤图象是与y= -x+4平行的直线.其中正确的说法有( )A.5个 B.4个 C.3个 D.2个二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了_____米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
10.关于函数y= -x-3的图象,有如下说法:①图象过点(0,-3);②图象与x轴的交点是(-3,0);③由图象可知y随x的增大而增大; ④图象不经过第一象限;⑤图象是与y= -x+4平行的直线.其中正确的说法有( )A.5个 B.4个 C.3个 D.2个二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了_____米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)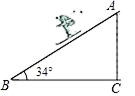 12.若分式
12.若分式 ![]() 的值为零,则x=________.13.若数据8,9,7,8,x,3的平均数是7,则这组数据的众数是________.14.若
的值为零,则x=________.13.若数据8,9,7,8,x,3的平均数是7,则这组数据的众数是________.14.若![]() 是
是![]() 的小数部分,则
的小数部分,则![]() 的值是______.15.已知矩形
的值是______.15.已知矩形![]() ,给出三个关系式:①
,给出三个关系式:①![]() ②
②![]() ③
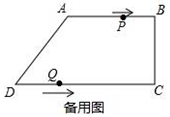
③![]() 如果选择关系式__________作为条件(写出一个即可),那么可以判定矩形为正方形,理由是_______________________________ .16.某种分子的半径大约是0.0000108mm,用科学记数法表示为______________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).(1)求CD的长;(2)当四边形PBQD为平行四边形时,求t的值;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理
如果选择关系式__________作为条件(写出一个即可),那么可以判定矩形为正方形,理由是_______________________________ .16.某种分子的半径大约是0.0000108mm,用科学记数法表示为______________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).(1)求CD的长;(2)当四边形PBQD为平行四边形时,求t的值;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理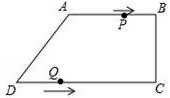
 18.(8分)三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了“二十四节气之旅”项目,并开展了相关知识竞赛.该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查.收集数据如下:七年级:
18.(8分)三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了“二十四节气之旅”项目,并开展了相关知识竞赛.该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查.收集数据如下:七年级:![]() 八年级:
八年级:![]() 整理数据如下:
整理数据如下: 分析数据如下:
分析数据如下: 根据以上信息,回答下列问题: (1)a=______,b=______;(2)你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性);(3)学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有_____人. 19.(8分)如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在BD上,OE=OF.(1)求证:AE=CF.(2)若AB=2,∠AOD=120°,求矩形ABCD的面积.
根据以上信息,回答下列问题: (1)a=______,b=______;(2)你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性);(3)学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有_____人. 19.(8分)如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在BD上,OE=OF.(1)求证:AE=CF.(2)若AB=2,∠AOD=120°,求矩形ABCD的面积.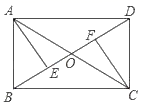 20.(8分)如图,矩形 ABCD 中,AB 4, BC 10, E 在 AD 上,连接 BE, CE, 过点 A 作 AG // CE ,分别交 BC, BE 于点 G, F , 连接 DG 交 CE 于点 H .若 AE 2, 求证:四边形 EFGH 是矩形.
20.(8分)如图,矩形 ABCD 中,AB 4, BC 10, E 在 AD 上,连接 BE, CE, 过点 A 作 AG // CE ,分别交 BC, BE 于点 G, F , 连接 DG 交 CE 于点 H .若 AE 2, 求证:四边形 EFGH 是矩形. 21.(8分)如图,在坐标系中,△ABC中A(-2,-1)、B(-3,-4)、C(0,-3).(1)请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标;(2)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标.
21.(8分)如图,在坐标系中,△ABC中A(-2,-1)、B(-3,-4)、C(0,-3).(1)请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标;(2)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标. 22.(10分)如图,在四边形
22.(10分)如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒
同时以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() 为多少秒时,以点
为多少秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形. 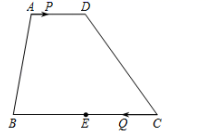 23.(10分)计算:(1)
23.(10分)计算:(1)![]() ;(2)
;(2)![]() 24.(12分)某商品的进价为每件40元,售价每件不低于60元且不高于80元,当售价为每件60元时,每个月可卖出100件;经调查发现,每件商品每上涨1元,每月少卖出2件.设每件商品的售价为x元(x为正整数).(1)求每个月的销售利润;(用含有x代数式表示)(2)若每个月的利润为2250元,定价应为多少元? 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、A4、A5、B6、C7、D8、B9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、1.12、213、7,114、115、① 一组邻边相等的矩形是正方形 16、1.08×10-5 三、解下列各题(本大题共8小题,共72分)17、(1)1;(2)2;(3)不存在.理由见解析18、 (1)8,88.1; (2)你认为 八 年级知识竞赛的总体成绩较好,理由1:理由2:见解析;或者你认为 七 年级知识竞赛的总体成绩较好,理由1: 理由2: 见解析; (答案不唯一,合理即可);(3)460.19、(1)见解析;(2)4
24.(12分)某商品的进价为每件40元,售价每件不低于60元且不高于80元,当售价为每件60元时,每个月可卖出100件;经调查发现,每件商品每上涨1元,每月少卖出2件.设每件商品的售价为x元(x为正整数).(1)求每个月的销售利润;(用含有x代数式表示)(2)若每个月的利润为2250元,定价应为多少元? 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、A4、A5、B6、C7、D8、B9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、1.12、213、7,114、115、① 一组邻边相等的矩形是正方形 16、1.08×10-5 三、解下列各题(本大题共8小题,共72分)17、(1)1;(2)2;(3)不存在.理由见解析18、 (1)8,88.1; (2)你认为 八 年级知识竞赛的总体成绩较好,理由1:理由2:见解析;或者你认为 七 年级知识竞赛的总体成绩较好,理由1: 理由2: 见解析; (答案不唯一,合理即可);(3)460.19、(1)见解析;(2)4![]() 20、证明见解析.21、(1)画图略,A’(2,1)(2)(1,0)或(-1,-6)或(-5,-2)22、当运动时间
20、证明见解析.21、(1)画图略,A’(2,1)(2)(1,0)或(-1,-6)或(-5,-2)22、当运动时间![]() 为
为![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.23、(1)
为顶点的四边形是平行四边形.23、(1)![]() (2)
(2)![]() 24、(1)﹣2x2+300x﹣8800;(2)若每个月的利润为2250元,定价应为65元.
24、(1)﹣2x2+300x﹣8800;(2)若每个月的利润为2250元,定价应为65元.
相关试卷
这是一份浙江省慈溪市(区域联考)2023-2024学年数学九年级第一学期期末学业水平测试试题含答案,共7页。试卷主要包含了下列图形中,成中心对称图形的是等内容,欢迎下载使用。
这是一份2023-2024学年浙江省慈溪市(区域联考)八年级数学第一学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了计算,已知等腰三角形的两边长满足+等内容,欢迎下载使用。
这是一份浙江省宁波市慈溪市阳光实验中学2022-2023学年七下数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了如图,点A是反比例函数等内容,欢迎下载使用。








