数学八年级上册12.2 三角形全等的判定教学设计

12.2.2《三角形全等的判定(2)》教案

一、教学目标

(一)知识与技能：1.掌握三角形全等的“SAS”条件；2.能运用“SAS”证明简单的三角形全等问题.

(二)过程与方法：经历探索三角形全等条件的过程，培养学生观察分析图形能力、动手能力.

(三)情感态度与价值观：通过对问题的共同探讨，培养学生的协作精神.

二、教学重点、难点

重点：应用“边角边”证明两个三角形全等，进而得出线段或角相等.

难点：指导学生分析问题，寻找判定三角形全等的条件.

三、教学过程

两边一角

如果已知一个三角形的两边及一角，那么有几种可能的情况呢？每种情况下的两边及一角分别相等的两个三角形是否全等？

1.边 角 边                      2.边 边 角

探究3

先任意画出一个△ABC，再画一个△A′B′C′，使A′B′=AB，A′C′=AC，∠A′=∠A(即两边和它们的夹角分别相等). 把画好的△A′B′C′剪下，放到△ABC上，它们全等吗？

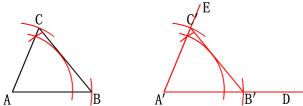
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).

定理应用格式：

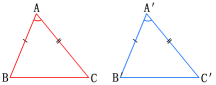在△ABC和△A′B′C′中，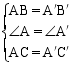

∴ △ABC≌△A′B′C′(SAS)

例2 如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B. 连接AC并延长到点D，使CD=CA. 连接BC并延长到点E，使CE=CB. 连接DE，那么量出DE的长就是A、B的距离，为什么？

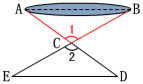证明：在△ABC和△DEC中，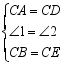

∴ △ABC≌△DEC (SAS)
∴ AB=DE

思考

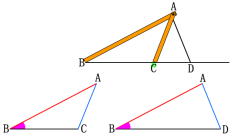    如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC. 固定住长木棍，转动短木棍，得到△ABD. 这个实验说明了什么？

    △ABC与△ABD满足两边和其中一边的对角分别相等，即AB=AB，AC=AD，∠B=∠B，但△ABC与△ABD不全等. 这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.

练习

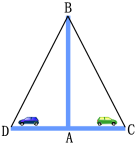1.如图，两车从南北方向的路段AB的A端出发，分别向东、向西行进相同的距离，到达C，D两地. 此时C，D到B的距离相等吗？为什么？

解：BC=BD. 理由如下：
在△ABC和△ABD中，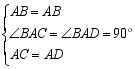

∴ △ABC≌△ABD (SAS)
∴ BC=BD

2.如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C. 求证∠A=∠D.

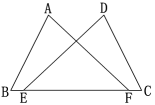证明：∵ BE=CF
∴ BE+EF=CF+EF
即 BF=CE
在△ABF和△DCE中，

∴ △ABF≌△DCE (SAS)
∴ ∠A=∠D

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    本节课从操作探究入手，具有较强的操作性和直观性，有利于学生从直观上积累感性认识，从而有效地激发了学生的学习积极性和探究热情，提高了课堂的教学效率，促进了学生对新知识的理解和掌握.