

人教版八年级上册12.2 三角形全等的判定教案设计
展开12.2.3《三角形全等的判定(3)》教案
一、教学目标
(一)知识与技能:1.掌握已知三角形两个内角和一条边的长度怎么画三角形;2.掌握三角形全等的证明方法:“角边角”和“角角边”;3.能熟练运用其进行证明.
(二)过程与方法:学生经历探索三角形全等条件的过程,体会如何探索研究问题,让学生通过探究,体会分类讨论的思想.
(三)情感态度与价值观:通过探究全等三角形的证明方法,体会分类讨论的思想,有助于学生形成严谨的学习习惯以及形成较强的逻辑推理能力.
二、教学重点、难点
重点:探究三角形全等的条件:角边角、角角边.
难点:运用角边角或角角边判定两个三角形全等.
三、教学过程
创设情境
如图,小黑熊不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?

探究4
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等). 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
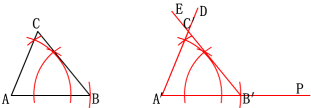
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
定理应用格式:
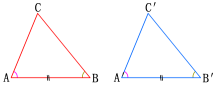 在△ABC和△A′B′C′中,
在△ABC和△A′B′C′中,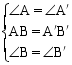
∴ △ABC≌△A′B′C′(ASA)
例3 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 求证AD=AE.
证明:
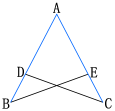 在△ACD和△ABE中,
在△ACD和△ABE中,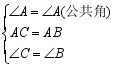
∴ △ACD≌△ABE (ASA)
∴ AD=AE
例4 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,求证△ABC≌△DEF.
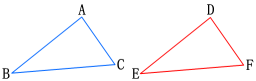 证明:在△ABC中,∠A+∠B+∠C=180°
证明:在△ABC中,∠A+∠B+∠C=180°
∴ ∠C=180°-∠A-∠B
同理∠F=180°-∠D-∠E
又∵ ∠A=∠D,∠B=∠E
∴ ∠C=∠F
在△ABC和△DEF中,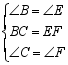
∴ △ABC≌△DEF (ASA)
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
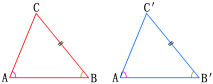 定理应用格式:
定理应用格式:
在△ABC和△A′B′C′中,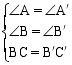
∴ △ABC≌△A′B′C′(AAS)
归纳
三边分别相等的两个三角形全等.(“边边边”或“SSS”).
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
练习
1.如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证AB=AD.
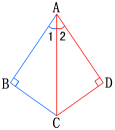 证明:∵ AB⊥BC,AD⊥DC
证明:∵ AB⊥BC,AD⊥DC
∴ ∠B=∠D=90°
在△ABC和△ADC中,
∴ △ABC≌△ADC (AAS)
∴ AB=AD
2.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长.为什么?
解:∵ AB⊥BF,DE⊥BF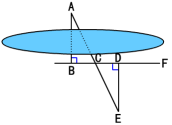 ∴ ∠ABC=∠EDC=90°
∴ ∠ABC=∠EDC=90°
在△ABC和△EDC中,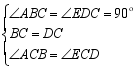
∴ △ABC≌△EDC (ASA)
∴ AB=ED
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
四、教学反思
本节课的教学借助于动手操作、分组讨论等探究出三角形全等的判定方法. 在寻找判定方法证明两个三角形全等的条件时,可先把容易找到的条件列出来,然后再根据判定方法去寻找所缺少的条件. 从课堂教学的情况来看,学生对“角边角”掌握较好,达到了教学的预期目的. 存在的问题是少数学生在方法“AAS”和“ASA”的选择上混淆不清,还需要在今后的教学中进一步加强巩固和训练.
初中华师大版第12章 整式的乘除12.2 整式的乘法3 多项式与多项式相乘教案设计: 这是一份初中华师大版第12章 整式的乘除12.2 整式的乘法3 多项式与多项式相乘教案设计,共3页。教案主要包含了情境导入,合作探究,板书设计等内容,欢迎下载使用。
数学八年级上册12.2 三角形全等的判定公开课教学设计: 这是一份数学八年级上册12.2 三角形全等的判定公开课教学设计,文件包含人教版初中数学八年级上册1223全等三角形判定方法ASAAAS课件pptx、人教版初中数学八年级上册1223全等三角形判定方法ASAAAS教案docx等2份教案配套教学资源,其中教案共8页, 欢迎下载使用。
初中沪科版14.2 三角形全等的判定教学设计: 这是一份初中沪科版14.2 三角形全等的判定教学设计,共3页。教案主要包含了教学内容,教学目标,教学重点,教学难点,教学过程等内容,欢迎下载使用。













