初中12.3 角的平分线的性质教案设计

12.3.1《角的平分线的性质(1)》教案

一、教学目标

(一)知识与技能：1.会作已知角的平分线；2.了解角的平分线的性质,能利用三角形全等证明角的平分线的性质；3.会利用角的平分线的性质进行证明与计算.

(二)过程与方法：在探究作角的平分线的方法及角的平分线的性质的过程中，进一步发展学生的推理证明意识和能力.

(三)情感态度与价值观：在探究作角的平分线的方法及角的平分线的性质的过程中，培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神，增强解决问题的信心，获得解决问题的成功体验.

二、教学重点、难点

重点：角的平分线的性质的证明及应用.

难点：角的平分线的性质的探究.

三、教学过程

知识回顾

1.角平分线的概念

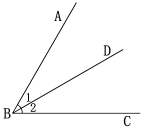
    从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线.

    ∵ ∠1=∠2
    ∴ BD是∠ABC的平分线

2.通过折纸的方法做一个角的平分线

思考

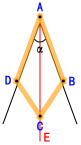
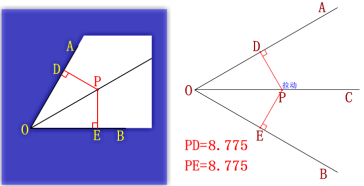
右边是利用角平分仪平分一个角的演示过程.

你能说明它的道理吗？其中AB=AD，BC=DC.

则：AE为∠α的角平分线.

证明：

在△ABC与△ADC中，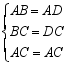

∴ △ABC≌△ADC (SSS)
∴ ∠BAC=∠DAC
即 AE是∠α的角平分线

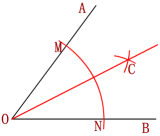用尺规作角的平分线.
已知：∠AOB.
求作：∠AOB的平分线.

作法：
1.以O为圆心，适当长为半径画弧，交OA于点M，交OB于点N.
2.分别以M，N为圆心，大于MN的长为半径画弧，两弧在∠AOB内部相交于点C.
3.画射线OC.
则：射线OC即为所求.

请你说明OC为什么是∠AOB的平分线.

思考

通过观察，你发现了角的平分线的什么性质？

点P在∠AOB的平分线OC上.

角平分线上的点到角的两边的距离相等.

你能利用三角形全等证明这个性质吗？

已知:_________________________________
求证:_________________________________

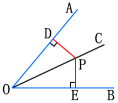如图，∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别是D，E. 求证PD=PE.

证明：∵ PD⊥OA，PE⊥OB
    ∴ ∠PDO=∠PEO=90°
    在△PDO和△PEO中，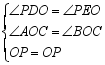

∴ △PDO≌△PEO (AAS)
∴ PD=PE

定理应用格式：

∵ 点P在∠AOB的平分线上，且PD⊥OA，PE⊥OB.
∴ PD=PE

归纳

一般情况下，我们要证明一个几何命题时，可以按照类似的步骤进行，即

1.明确命题中的已知和求证；

2.根据题意，画出图形，并用数学符号表示已知和求证；

3.经过分析，找出由已知推出要证的结论的途径，写出证明过程.

练习

如图，在直线MN上求作一点P，使点P到射线OA和OB的距离相等.

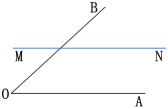
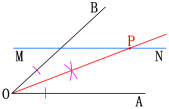
则：点P为所求.

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    本节课由于采用了动手操作以及讨论交流等教学方法，从而有效地增强了学生对角以及角平分线的性质的感性认识，提高了学生对新知识的理解与感悟，因而本节课的教学效果较好，学生对所学的新知识掌握较好，达到了教学的目的. 不足之处是少数学生在性质的运用上还存在问题，需要在今后的教学与作业中进一步的加强巩固和训练.