

初中数学人教版八年级上册13.4课题学习 最短路径问题教学设计
展开13.4《最短路径问题》教案
一、教学目标
(一)知识与技能:通过对最短路径的探素,进一步理解和掌握两点之间线段最短和垂线段最短的性质.
(二)过程与方法:让学生经历运用所学知识解决问题的过程,培养学生解决问题的能力,掌握探索最短路径的思想方法.
(三)情感态度与价值观:在数学学习活动中,获得成功的体验,树立自信心.
二、教学重点、难点
重点:应用所学知识解决最短路径问题.
难点:选择合理的方法解决问题.
三、教学过程
引言
以前我们研究过一些关于“两点的所有连线中,线段最短”“连接直线外一点与直线上各点的所有线段中,垂线段最短”等的问题,我们称它们为最短路径问题.现实生活中经常涉及到选择最短路径的问题,本节将利用数学知识探究数学史中著名的“将军饮马问题”及“造桥选址问题”.

问题1 相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦. 有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:
如图,牧马人从A地出发,到一条笔直的河边 l 饮马,然后到B地. 牧马人到河边什么地方饮马,可使所走的路径最短?
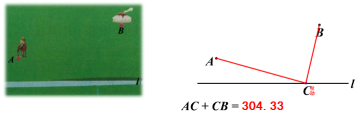
如图,点A,B分别是直线 l 异侧的两个点,如何在 l 上找到一个点C,使得点C到点A、点B的距离的和最短?
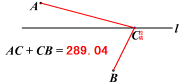

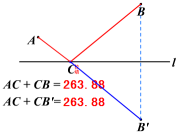
连接AB,与直线 l 相交于一点,根据“两点之间,线段最短”可知这个交点即为所求.
现在,要解决的问题是:点A,B分别是直线 l 同侧的两个点,如何在 l 上找到一个点,使得这个点到点A、点B的距离的和最短?
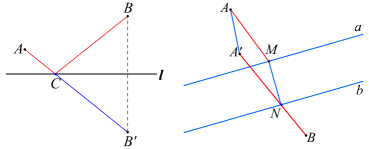
如图,作出点B关于 l 的对称点B',利用轴对称的性质,可以得到CB'=CB. 这样,问题就转化为:当点C在 l 的什么位置时,AC与CB'的和最小?
在连接A,B'两点的线中,线段AB'最短. 因此,线段AB'与直线 l 的交点C的位置即为所求.
你能用所学的知识证明AC+BC最短吗?
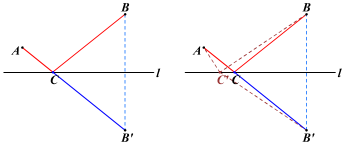
证明:如图,在直线 l 上任取一点C′(与点C不重合),连接AC′,BC′,B′C′.
由轴对称的性质知,BC=B′C,BC′=B′C′.
∴ AC+BC=AC+B′C=AB′
AC′+BC′=AC′+B′C′
在△AB′C′中,AB′<AC′+B′C′
∴ AC+BC<AC′+BC′
即AC+BC最短.
问题2 (造桥选址问题)如图,A和B两地在一条河的两岸,现要河上造一座桥MN. 桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)
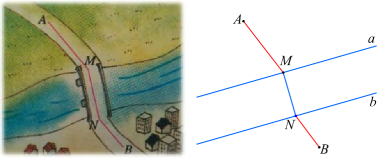
我们可以把河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M,这样,上面的问题可以转化为下面的问题:当点N在直线b的什么位置时,AM+MN+NB最小?
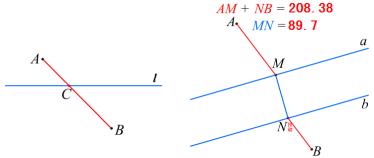
由于河岸宽度是固定的,因此当AM+NB最小时,AM+MN+NB最小. 这样问题就进一步转化为:当点N在直线b的什么位置时,AM+NB最小?能否通过图形的变化(轴对称、平移等),把右图的情况转化为左图的情况?
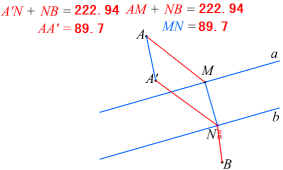
如图,将AM沿与河岸垂直的方向平移,点M移动到点N,点A移动到点A′,则AA′=MN,AM+NB=A′N+NB. 这样问题就转化为:当点N在直线b的什么位置时,A′N+NB最小?
在连接A′,B两点线中,线段A′B最短. 因此,线段A′B与直线b的交点N的位置即为所求,即在点N处造桥MN,所得路径AMNB是最短的.
你能用所学的知识证明AM+MN+NB最短吗?
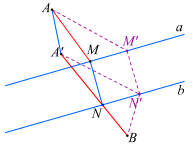
为了证明点N的位置即为所求,我们不妨在直线b上另外任意取一点N′,过N′作N′M′⊥a,垂足为M′,连接AM′,A′N′,N′B,证明AM+MN+NB<AM′+M′N′+N′B.
证明:如图,由平移的性质可知:
AM=A′N,AM′=A′N′,MN=M′N′
在△A′BN′中,A′B<A′N′+N′B
∴ A′N+NB<AM′+N′B
∴ AM+NB<AM′+N′B
∴ AM+MN+NB<AM′+M′N′+N′B
归纳
在解决最短路径问题时,我们通常利用轴对称、平移等变化把已知问题转化为容易解决的问题,从而作出最短路径的选择.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
四、教学反思
通过本节课进一步体会数学与自然及人类社会的密切联系,了解数学的价值. 在互动交流活动中,学习从不同角度理解问题,寻求解决问题的方法,并有效地解决问题. 体会在解决问题中与他人合作的重要性. 体会运用数学的思维方式观察、分析现实社会,解决日常生活中和其他学科中的问题,增强应用数学的意识.
初中数学人教版八年级上册13.4课题学习 最短路径问题教案设计: 这是一份初中数学人教版八年级上册13.4课题学习 最短路径问题教案设计,共12页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
人教版八年级上册13.4课题学习 最短路径问题优秀教案: 这是一份人教版八年级上册13.4课题学习 最短路径问题优秀教案,共5页。教案主要包含了教学目标,重点难点,教学过程等内容,欢迎下载使用。
初中数学人教版八年级上册13.4课题学习 最短路径问题教案: 这是一份初中数学人教版八年级上册13.4课题学习 最短路径问题教案,共5页。教案主要包含了教学目标,教学重点及难点,教学用具,相关资源,教学过程,课堂小结,板书设计等内容,欢迎下载使用。













