初中数学人教版八年级上册14.2.1 平方差公式教案

14.2.1《平方差公式》教案

一、教学目标

(一)知识与技能：会推导平方差公式，并且懂得运用平方差公式进行简单计算.

(二)过程与方法：经历探索特殊形式的多项式乘法的过程，发展学生的符号感和推理能力，使学生逐渐掌握平方差公式.

(三)情感态度与价值观：通过合作学习，体会在解决具体问题过程中与他人合作的重合性，体验数学活动充满着探索性和创造性.

二、教学重点、难点

重点：平方差公式的推导和运用，以及对平方差公式的几何背景的了解.

难点：平方差公式的应用.

三、教学过程

创设情境

    灰太狼开了一家租地公司，一天他把一边长为 a 米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米，另一边减少5米，再继续租给你，租金不变，这样你也没吃亏，你看如何？”慢羊羊一听觉得没有吃亏，就答应了. 慢羊羊回到羊村，就把这件事对喜羊羊他们讲了，喜羊羊一听，马上说道:“村长，您吃亏了!”慢羊羊村长很吃惊的问道:“啊! 那我吃亏了多少？”沸羊羊说道:“我来帮您算算.”喜羊羊还没等沸羊羊开始算就说道:“不用算了，村长亏了25米2.”沸羊羊不解道:“你怎么这么快啊!”

探究

计算下列多项式的积，你能发现什么规律？

(1) (x+1)(x-1)=_______；(2) (m+2)(m-2)=______；(3) (2x+1)(2x-1)=_______.

计算：(a+b)(a-b)=a2-ab+ab-b2=a2-b2

平方差公式：(a+b)(a-b)=a2-b2，两个数的和与这两个数的差的积，等于这两个数的平方差.

思考

根据下面的演示，你能通过求阴影部分的面积说明平方差公式吗？

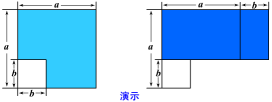
分析：(1) 左图中阴影部分的面积为_______；(2) 将阴影部分拼成右图的一个长方形，这个长方形的长是____，宽是____，面积___________.

例1 运用平方差公式— (a+b)(a-b)=a2-b2 计算：

(1) (3x+2)(3x-2)    (2) (-x+2y)(-x-2y)

分析：在(1)中，可以把 3x 看成 a ，2 看成 b ，即

      (3x + 2)(3 x - 2)=(3x)2-22

      (a + b)(a - b)= a2 - b2

解：(1) (3x+2)(3x-2) =(3x)2-22= 9x2-4

(2) (-x+2y)(-x-2y) =(-x)2-(2y)2= x2-4y2

观察

(1)计算下列各组算式，并观察它们的共同特点.

(2)从上的过程中，你发现了什么规律？

三个连续整数中，首尾两数的积，等于中间数的平方减1.

(3)这一规律用字母可表示为___________________，它的正确性可用_____________说明.

例2 计算：

(1) (y+2)(y-2)-(y-1)(y+5)    (2) 102×98

解：(1) (y+2)(y-2)-(y-1)(y+5) =y2-22-(y2+4y-5) =y2-4-y2-4y+5=-4y+1

(2) 102×98=(100+2)×(100-2) =1002-22=10000-4=9996

(y-1)(y+5)= (y2-5)？

(只有符合公式条件的乘法，才能运用公式简化运算，其余的运算仍按乘法法则进行.)

练习

1.下面各式的计算对不对？如果不对，应当怎样改正？

(1) (x+2)(x-2)=x2-2  (    ) 改正：_____________________.

(2) (-3a-2)(3a-2)=9a2-4 (    ) 改正：_____________________.

2.运用平方差公式计算：

(1) (a+3b)(a-3b)  (2) (3+2a)(-3+2a)

(3) 51×49        (4) (3x+4)(3x-4)-(2x+3)(3x-2)

解：(1)原式=a2-(3b)2=a2-9b2

(2)原式=(2a+3)(2a-3)=(2a)2-32=4a2-9

(3)原式=(50+1)×(50-1)=502-12=2500-1=2499

(4)原式=(3x)2-42-(6x2-4x+9x-6) =9x2-16-6x2+4x-9x+6=3x2-5x-10

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    学生通过“做一做”发现平方差公式，同时通过“试一试”用几何方法证明公式的正确性. 通过这两种方式的演算，让学生理解平方差公式．本节教学内容较多，因此教材中的练习可以让学生在课后完成.