初中数学14.2.2 完全平方公式教学设计及反思

14.2.2《完全平方公式》教案

一、教学目标

(一)知识与技能：理解完全平方公式，能用公式进行计算.

(二)过程与方法：经历探索完全平方公式的过程，进而感受特殊到一般、数形结合思想，发展符号意识和几何直观观念.

(三)情感态度与价值观：通过完全平方公式的应用，体会公式中字母的含义，渗透整体、数形结合、类比的数学思想.

二、教学重点、难点

重点：完全平方公式的推导过程，结构特点与公式的应用.

难点：完全平方公式结构特点及其应用.

三、教学过程

创设情境

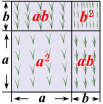    一块边长为a米的正方形实验田，因其边长增加b米，形成四块实验田，以种植不同的新品种.
    你能用不同的方法表示试验田的总面积吗？

①总面积=(a+b) 2

②总面积=a2+ab+ab+b2=a2+2ab+b2

你发现了什么？(a+b)2=a2+2ab+b2

探究

计算下列各式，你能发现什么规律？

(1) (p+1)2=(p+1)(p+1)=_________；(2) (m+2)2=_________；

(3) (p-1)2=(p-1)(p-1)=_________；(4) (m-2)2=_________.

计算：(a+b)2，(a-b)2.

(a+b)2=(a+b)(a+b) =a2+ab+ab+b2=a2+2ab+b2

(a-b)2=(a-b)(a-b) =a2-ab-ab+b2=a2-2ab+b2

完全平方公式

(a＋b)2=a2＋2ab＋b2，(a－b)2=a2－2ab＋b2.可以合写成 (a±b)2=a2±2ab＋b2

两个数的和(或差)的平方，等于它们的平方和，加上(或减去)它们的积的2倍.

注：公式中的字母a、b可以表示数、单项式和多项式.

思考

你能根据图(1)和图(2)中图形的面积说明完全平方公式吗？

例3 运用完全平方公式计算：

(1) (4m+n)2   (2)

解：(1) (4m+n)2=(4m)2+2·(4m)·n+n2=16m2+8mn+n2

(2) =y2-2·y·+= y2-y+

例4 运用完全平方公式计算：

(1) 1022  (2) 992

解：(1) 1022=(100+2)2=1002+2×100×2+22=10000+400+4=10404

(2) 992=(100-1)2=1002-2×100×1+12=10000-200+1=9801

思考

(a+b)2与(-a-b)2相等吗？(a-b)2与(b-a)2相等吗？(a-b)2与a2-b2相等吗？为什么？

(-a-b)2=(-a)2-2·(-a) b+b2=a2+2ab+b2=(a+b)2

(b-a)2=b2-2ba+a2=a2-2ab+b2=(a-b)2

(a-b)2与a2-b2不一定相等.只有当b=0或a=b时，(a-b)2=a2-b2.

练习

1.运用完全平方公式计算：

(1) (x+6)2    (2) (y-5)2    (3) (-2x+5)2    (4)

解：(1)原式= x2+2·x·6+62 = x2+12x+36

(2)原式= y2-2·y·5+52 = y2-10y+25

(3)原式=(5-2x)2 = 52-2·5·2x+(2x)2 = 25-20x+4x2

(4)原式=-2··+=

2.下面各式的计算错在哪里？应当怎样改正？

(1) (a+b)2=a2+b2  改正：__________________；

(2) (a-b)2=a2-b2  改正：__________________.

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    本节的探讨方式和上节类似，都是通过“做一做”和“试一试”让学生在代数和几何两方面理解完全平方公式. 完全平方公式分为两数和的平方和两数差的平方两种形式，教学中可以将两个公式写作一个公式：(a±b)2＝a2±2ab＋b2，有助于学生的记忆. 在探究两数差的平方公式时，因为学生通过前面的学习已经掌握了几何的说明方法，因此可以让学生自己画图证明.