


浙江省杭州市高桥2022-2023学年七下数学期末质量检测试题含答案
展开
这是一份浙江省杭州市高桥2022-2023学年七下数学期末质量检测试题含答案,共7页。
浙江省杭州市高桥2022-2023学年七下数学期末质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是 A.S1>S2 B.S1=S2 C.S1<S2 D.3S1=2S22.若关于
A.S1>S2 B.S1=S2 C.S1<S2 D.3S1=2S22.若关于![]() 的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )A.
的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )A.![]() B.1 C.
B.1 C.![]() D.
D.![]() 3.从2004年5月起某次列车平均提速20千米/小时,用相同的时间,列车提速前行驶200千米,提速后比提速前多行驶50千米,提速前列车的平均速度是多少?设提速前这次列车的平均速度为
3.从2004年5月起某次列车平均提速20千米/小时,用相同的时间,列车提速前行驶200千米,提速后比提速前多行驶50千米,提速前列车的平均速度是多少?设提速前这次列车的平均速度为![]() 千米/小时,则下列列式中正确的是( )A.
千米/小时,则下列列式中正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )A.b2﹣c2=a2 B.a:b:c=3:4:5C.∠A:∠B:∠C=9:12:15 D.∠C=∠A﹣∠B5.如图,在
4.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )A.b2﹣c2=a2 B.a:b:c=3:4:5C.∠A:∠B:∠C=9:12:15 D.∠C=∠A﹣∠B5.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D为AB上的动点,连接CD,以AD、CD为边作平行四边形ADCE,则DE长的最小值为( )
,D为AB上的动点,连接CD,以AD、CD为边作平行四边形ADCE,则DE长的最小值为( )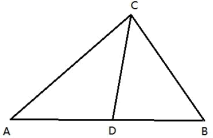 A.3 B.4 C.
A.3 B.4 C.![]() D.
D.![]() 6.如图,在平面直角坐标系中,点
6.如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )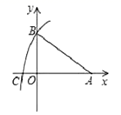 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,▱ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是( )
7.如图,▱ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是( )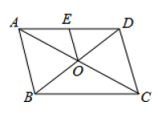 A.18 B.10 C.9 D.88.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
A.18 B.10 C.9 D.88.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2017秒时点P的坐标是( )
个单位长度,则第2017秒时点P的坐标是( )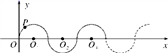 A.(2016,0) B.(2017,1) C.(2017,-1) D.(2018,0)9.如图1,在矩形ABCD中,动点E从点B出发,沿BADC方向运动至点C处停止,设点E运动的路程为x,△BCE的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长为( )
A.(2016,0) B.(2017,1) C.(2017,-1) D.(2018,0)9.如图1,在矩形ABCD中,动点E从点B出发,沿BADC方向运动至点C处停止,设点E运动的路程为x,△BCE的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长为( )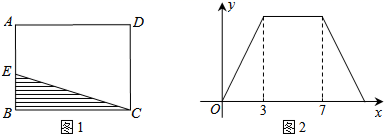 A.20 B.21 C.14 D.710.下列二次根式中,属于最简二次根式的是
A.20 B.21 C.14 D.710.下列二次根式中,属于最简二次根式的是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.若关于x的分式方程
二、填空题(本大题共有6小题,每小题3分,共18分)11.若关于x的分式方程![]() 无解,则m的值为__________.12.如图是一块地的平面示意图,已知AD=4 m,CD=3 m,AB=13 m,BC=12 m,∠ADC=90°,则这块地的面积为_____m2.
无解,则m的值为__________.12.如图是一块地的平面示意图,已知AD=4 m,CD=3 m,AB=13 m,BC=12 m,∠ADC=90°,则这块地的面积为_____m2.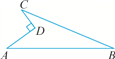 13.
13.![]() 成立的条件是___________________.14.如图,一次函数
成立的条件是___________________.14.如图,一次函数![]() 的图象经过点
的图象经过点![]() ,则关于
,则关于![]() 的一元一次方程
的一元一次方程![]() 的解为___________.
的解为___________.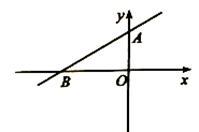 15.如图,矩形ABCD中,
15.如图,矩形ABCD中,![]() ,
,![]() ,CB在数轴上,点C表示的数是
,CB在数轴上,点C表示的数是![]() ,若以点C为圆心,对角线CA的长为半径作弧交数轴的正半轴于点P,则点P表示的数是______.
,若以点C为圆心,对角线CA的长为半径作弧交数轴的正半轴于点P,则点P表示的数是______.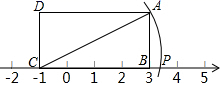 16.如图,已知
16.如图,已知![]() ,
,![]() 与
与![]() 之间的距离为3,
之间的距离为3, ![]() 与
与![]() 之间的距离为6,
之间的距离为6, ![]() 分别等边三角形
分别等边三角形![]() 的三个顶点,则此三角形的边长为__________.
的三个顶点,则此三角形的边长为__________.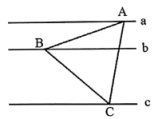 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.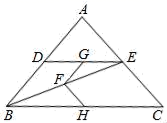 18.(8分)如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线
18.(8分)如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线![]() (x>0)与OA边交于点D、与AB边交于点E.(1)求点D的坐标;(2)求证:四边形ABCD是正方形;(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.
(x>0)与OA边交于点D、与AB边交于点E.(1)求点D的坐标;(2)求证:四边形ABCD是正方形;(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.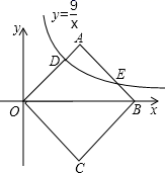 19.(8分)杨梅是漳州的特色时令水果.杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价每件比第一批多了5元.(1)第一批杨梅每件进价多少元?(2)老板以每件150元的价格销售第二批杨梅,售出
19.(8分)杨梅是漳州的特色时令水果.杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价每件比第一批多了5元.(1)第一批杨梅每件进价多少元?(2)老板以每件150元的价格销售第二批杨梅,售出![]() 后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润
后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润![]() 售价
售价![]() 进价)? 20.(8分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
进价)? 20.(8分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.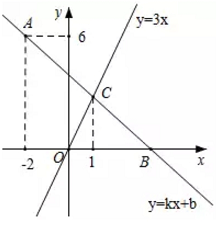 (1)求k,b的值;(2)请直接写出不等式kx+b﹣3x>0的解集;(3)M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标. 21.(8分)某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产
(1)求k,b的值;(2)请直接写出不等式kx+b﹣3x>0的解集;(3)M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标. 21.(8分)某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产![]() 、
、![]() 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件![]() 种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件![]() 种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元.设生产
种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元.设生产![]() 种产品的件数为
种产品的件数为![]() (件),生产
(件),生产![]() 、
、![]() 两种产品所获总利润为
两种产品所获总利润为![]() (元)(1)试写出
(元)(1)试写出![]() 与
与![]() 之间的函数关系式:(2)求出自变量
之间的函数关系式:(2)求出自变量![]() 的取值范围;(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少? 22.(10分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料? 23.(10分)春节前夕,某商店根据市场调查,用2000元购进第一批盒装花,上市后很快售完,接着又用4200元购进第二批这种盒装花.已知第二批所购的盒数是第一批所购花盒数的3倍,且每盒花的进价比第一批的进价少6元.求第一批盒装花每盒的进价. 24.(12分)某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.(1)求出y与m之间的函数关系式;(2)该商店如何进货才能获得最大利润?此时最大利润是多少元? 参考答案 一、选择题(每小题3分,共30分)1、B2、A3、B4、C5、D6、B7、C8、B9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、
的取值范围;(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少? 22.(10分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料? 23.(10分)春节前夕,某商店根据市场调查,用2000元购进第一批盒装花,上市后很快售完,接着又用4200元购进第二批这种盒装花.已知第二批所购的盒数是第一批所购花盒数的3倍,且每盒花的进价比第一批的进价少6元.求第一批盒装花每盒的进价. 24.(12分)某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.(1)求出y与m之间的函数关系式;(2)该商店如何进货才能获得最大利润?此时最大利润是多少元? 参考答案 一、选择题(每小题3分,共30分)1、B2、A3、B4、C5、D6、B7、C8、B9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、113、x≥114、
12、113、x≥114、![]() 15、
15、![]() 16、
16、![]() 三、解下列各题(本大题共8小题,共72分)17、 (1)证明见解析;(2)证明见解析;(3)∠GFH=100°.18、(1)点D的坐标为(1,1);(2)见解析;(1)
三、解下列各题(本大题共8小题,共72分)17、 (1)证明见解析;(2)证明见解析;(3)∠GFH=100°.18、(1)点D的坐标为(1,1);(2)见解析;(1)![]() .19、(1)120元(2)至少打7折.20、(1)k=﹣1,b=3;(3)x<1;(3)M点坐标为(3,3).21、(1)y与x之间的函数关系式是
.19、(1)120元(2)至少打7折.20、(1)k=﹣1,b=3;(3)x<1;(3)M点坐标为(3,3).21、(1)y与x之间的函数关系式是![]() ;(2)自变量x的取值范围是x = 30,31,1;(3)生产A种产品 30件时总利润最大,最大利润是2元,22、A型机器人每小时搬运
;(2)自变量x的取值范围是x = 30,31,1;(3)生产A种产品 30件时总利润最大,最大利润是2元,22、A型机器人每小时搬运![]() kg化工原料,B型机器人每小时搬运
kg化工原料,B型机器人每小时搬运![]() kg化工原料.23、20元24、(1)
kg化工原料.23、20元24、(1)![]() =﹣200
=﹣200![]() +15000(20≤m<30);(2) 购进A型电动自行车20辆,购进B型10辆,最大利润是11000元.
+15000(20≤m<30);(2) 购进A型电动自行车20辆,购进B型10辆,最大利润是11000元.
相关试卷
这是一份2023-2024学年浙江省杭州市高桥数学九上期末学业水平测试模拟试题含答案,共7页。试卷主要包含了以下事件为必然事件的是等内容,欢迎下载使用。
这是一份2023-2024学年浙江省杭州市杭州市萧山区高桥初级中学数学九年级第一学期期末质量检测模拟试题含答案,共9页。
这是一份浙江省杭州市余杭区国际学校2022-2023学年数学七下期末质量检测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,函数y=x-1的图象是,运行程序如图所示,规定等内容,欢迎下载使用。









