浙江省湖州市实验学校2022-2023学年七下数学期末考试试题含答案

浙江省湖州市实验学校2022-2023学年七下数学期末考试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．在平面直角坐标系中，若点P的坐标为（﹣3，2），则点P所在的象限是（　 　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

2．若直线y=x+1与y=-2x+a的交点在第一象限，则a的取值可以是

A．-1 B．0 C．1 D．2

3．如图，在菱形ABCD中，对角线AC，BD相交于点O. 下列结论中不一定成立的是（   ）

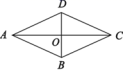
A．AB∥CD B．OA=OC

C．AC⊥BD D．AC=BD

4．如图所示，正方形纸片ABCD中，对角线AC，BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB，AC于点E，G，连接GF，给出下列结论：

①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数有（）

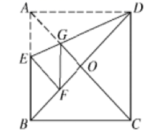
A．2个 B．4个 C．3个 D．5个

5．一组数据2，3，5，5，4的众数、中位数分别是（   ）

A．5，4 B．5，5 C．5，4.5 D．5，3.8

6．在平行四边形ABCD中，若∠B=135°，则∠D=（    ）

A．45° B．55° C．135° D．145°

7．下列说法正确的是（  ）

A．全等的两个图形成中心对称

B．成中心对称的两个图形必须能完全重合

C．旋转后能重合的两个图形成中心对称

D．成中心对称的两个图形不一定全等

8．在平面直角坐标系中，将点先向左平移个单位长度，再向下平移个单位长度，则平移后得到的点是（  ）

A． B． C． D．

9．用反证法证明“三角形中至少有一个内角大于或等于”时，应假设（     ）

A．三角形的二个内角小于 B．三角形的三个内角都小于

C．三角形的二个内角大于 D．三角形的三个内角都大于

10．2018年体育中考中，我班一学习小组6名学生的体育成绩如下表，则这组学生的体育成绩的众数，中位数依次为（　 　）

A．48，48 B．48，47.5 C．3，2.5 D．3，2

二、填空题(本大题共有6小题，每小题3分，共18分)

11．不等式2x-1>5的解集为               ．

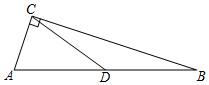
12．如图，点D是Rt△ABC斜边AB的中点，AC＝1，CD＝1．5，那么BC＝_____．

13．弹簧原长(不挂重物)15cm，弹簧总长L(cm)与重物质量x(kg)的关系如下表所示：

当重物质量为4kg（在弹性限度内）时，弹簧的总长L(cm)是_________．

14．如图，已知矩形的面积为，依次取矩形各边中点、、、，顺次连结各中点得到第个四边形，再依次取四边形各边中点、、、，顺次连结各中点得到第个四边形,……，按照此方法继续下去，则第个四边形的面积为________．

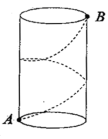
15．如图，圆柱体的高为8cm，底面周长为4cm，小蚂蚁在圆柱表面爬行，从A点到B点，路线如图所示，则最短路程为_____．

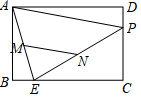
16．如图，矩形ABCD中，AB=6，BC=8，E是BC上一点（不与B、C重合），点P在边CD上运动，M、N分别是AE、PE的中点，线段MN长度的最大值是_____．

三、解下列各题(本大题共8小题，共72分)

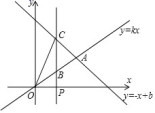
17．（8分）如图，已知在平面直角坐标系 xOy 中，正比例函数 y=kx 与一次函数 y=−x+b 的图象相交于点 A(4，3).过点 P(2，0)作 x 轴的垂线，分别交正比例函数的图象于点 B，交一次函数的图象于点 C， 连接 OC.

(1)求这两个函数解析式；

(2)求△OBC 的面积；

(3)在 x 轴上是否存在点 M，使△AOM 为等腰三角形? 若存在，直接写出 M 点的坐标；若不存在，请说明理由.

18．（8分）在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

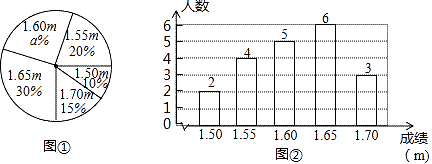
（Ⅰ）图1中a的值为　   　；

（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；

（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

19．（8分）如图，直线l的解析式为y=-x+，与x轴，y轴分别交于A，B两点，双曲线与直线l交于E，F两点，点E的横坐标为1.

(1)求k的值及F点的坐标;

(2)连接OE，OF，求△EOF的面积;

(3)若点P是EF下方双曲线上的动点(不与E，F重合)，过点P作x轴，y轴的垂线，分别交直线l于点M，N，求的值.

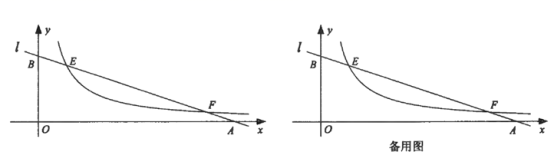
20．（8分）小明星期天从家里出发骑车去舅舅家做客，当他骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，以下是他本次去舅舅家所用的时间与路程的关系式示意图，根据图中提供的信息回答下列问题：

（1）小明家到舅舅家的路程是______米，小明在商店停留了______分钟；

（2）在整个去舅舅家的途中哪个时间段小明骑车速度最快，最快的速度是多少米/

分？

（3）本次去舅舅家的行程中，小明一共行驶了多少米？一共用了多少分钟？

21．（8分）已知反比例函数与一次函数y=kx+b的图象都经过点(-2，-1)，且当x=3时这两个函数值相等．

(1)求这两个函数的解析式；

(2)直接写出当x取何值时，成立．

22．（10分）下表给出三种上宽带网的收费方式.

设月上网时间为，方式的收费金额分别为，直接写出的解析式，并写出自变量的取值范围；

填空：当上网时间        时，选择方式最省钱；

当上网时间        时，选择方式最省钱；

当上网时间        时，选择方式最省钱；

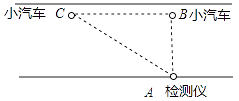
23．（10分） “中华人民共和国道路交通管理条例”规定：小汽车在高速公路上的行驶速度不得超过120千米/小时，不得低于60千米/小时，如图，一辆小汽车在高速公路上直道行驶，某一时刻刚好行驶到“车速检测点”正前方60米处，过了3秒后，测得小汽车位置与“车速检测点”之间的距离为100米，这辆小汽车是按规定行驶吗？

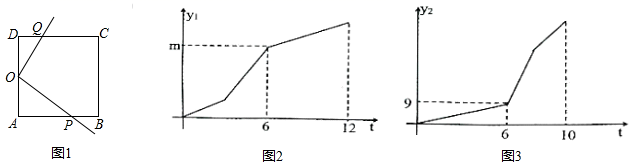
24．（12分）如图1在正方形中，是的中点，点从点出发沿的路线移动到点时停止，出发时以单位/秒匀速运动：同时点从出发沿的路线匀速运动，移动到点时停止，出发时以单位/秒运动,两点相遇后点运动速度变为单位/秒运动，点运动速度变为单位/秒运动：图2是射线随点运动在正方形中扫过的图形的面积与时间的函数图象，图3是射线随点运动在正方形中扫过的图形的面积与时间的图数图象，

（1）正方形的边长是______.

（2）求，相遇后在正方形中所夹图形面积与时间的函数关系式.

参考答案

一、选择题(每小题3分,共30分)

1、B

2、D

3、D

4、C

5、A

6、C

7、B

8、A

9、B

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、x>1

12、2

13、1

14、

15、10cm

16、5

三、解下列各题(本大题共8小题，共72分)

17、（1）y=x; y=−x+7;（2）;（3）存在，M（8,0），M（,0），M（,0），M（-,0）.

18、 (1) 25 ; (2) 这组初赛成绩数据的平均数是1.61.；众数是1.65；中位数是1.1；（3）初赛成绩为1.65 m的运动员能进入复赛.

19、（1）；（2）；（3）

20、（1）1500，4；（2）小明在12-14分钟最快，速度为米/分．（3）14.

21、（1）一次函数的解析式为；反比例函数解析式为；（2）x＜-2或0＜x＜3

22、;;;不超过； 超过而不超过； 超过.

23、这辆小汽车是按“中华人民共和国道路交通管理条例”规定行驶．̈

24、（1）6；（2）见详解.