


浙江省江北区2022-2023学年七年级数学第二学期期末调研试题含答案
展开浙江省江北区2022-2023学年七年级数学第二学期期末调研试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.一个多边形的每一个外角都等于40°,则这个多边形的内角和是.( )
A.360° B.980° C.1260° D.1620°
2.如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( )
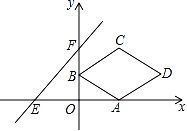
A.2 B.3 C.4 D.5
3.如图,矩形ABCD中,CD=6,E为BC边上一点,且EC=2将△DEC沿DE折叠,点C落在点C'.若折叠后点A,C',E恰好在同一直线上,则AD的长为( )
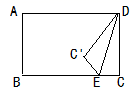
A.8 ![]() B.9
B.9 ![]() C.
C.![]()
![]() D.10
D.10
4.王老师在讲“实数”时画了一个图(如图),即“以数轴的单位长度的线段为边作一个正方形,然后以表示-1的点为圆心,正方形的对角线长为半径画弧交数轴于点A”.则数轴上点A所表示的数是( )
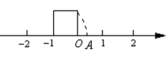
A.![]() -1 B.-
-1 B.-![]() +1 C.
+1 C.![]() D.-
D.-![]()
5.下列各组数中,不是勾股数的为( )
A.3,4,5 B.6,8,10 C.5,12,13 D.5,7,10
6.下列命题中,有几个真命题 ( )
①同位角相等 ②直角三角形的两个锐角互余
③平行四边形的对角线互相平分且相等 ④对顶角相等
A.1个 B.2个 C.3个 D.4个
7.反比例函数 y=![]() 的图象如图所示,点 M 是该函数图象上的一点,MN 垂直于 x 轴,垂足为 N,若 S△MON=
的图象如图所示,点 M 是该函数图象上的一点,MN 垂直于 x 轴,垂足为 N,若 S△MON=![]() ,则 k 的值为( )
,则 k 的值为( )
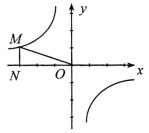
A.![]() B.
B.![]() C.3 D.-3
C.3 D.-3
8.若![]() =
=![]() ,则
,则![]() 的值是()
的值是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列等式不一定成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知a>b,c≠0,则下列关系一定成立的是( ).
A.ac>bc B.![]() C.c-a>c-b D.c+a>c+b
C.c-a>c-b D.c+a>c+b
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知![]() 是分式方程
是分式方程![]() 的根,那么实数
的根,那么实数![]() 的值是__________.
的值是__________.
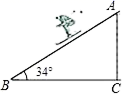
12.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了_____米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
13.若分式![]() 在实数范围内有意义,则x的取值范围是_____.
在实数范围内有意义,则x的取值范围是_____.
14.在函数![]() 中,自变量x的取值范围是________________.
中,自变量x的取值范围是________________.
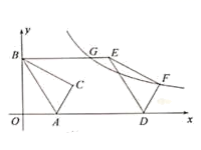
15.如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y=![]() 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .
上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .
16.为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为________.
三、解下列各题(本大题共8小题,共72分)
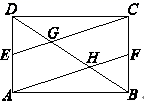
17.(8分)如图,矩形![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别交
分别交![]() 于
于![]() 两点.
两点.
求证:(1)四边形![]() 是平行四边形;
是平行四边形;
(2)![]() .
.
18.(8分)已知:如图,在![]() 中,
中,![]() 。
。
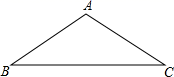
(1)尺规作图:作线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ;(保留作图痕迹,不写作法);
;(保留作图痕迹,不写作法);
(2)求证:![]() 是等腰三角形。
是等腰三角形。
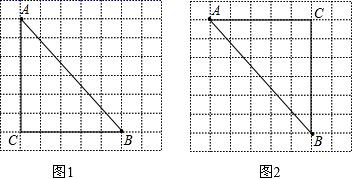
19.(8分)图l、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.点A和点B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个 即可);
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可);
20.(8分)解不等式组: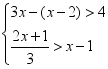 .并把它的解集在数轴上表示出来
.并把它的解集在数轴上表示出来
![]()
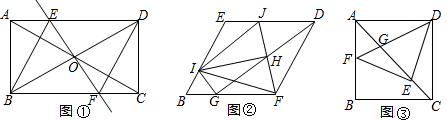
21.(8分) (1)如图①,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,交AD于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数;
(2)把(1)中菱形BFDE进行分离研究,如图②,点G、I分别在BF、BE边上,且BG=BI,连接GD,H为GD的中点,连接FH并延长,交ED于点J,连接IJ、IH、IF、IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图③,当矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE、EF、DF,使△DEF是等腰直角三角形,DF交AC于点G.请直接写出线段AG、GE、EC三者之间满足的数量关系.
22.(10分)为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
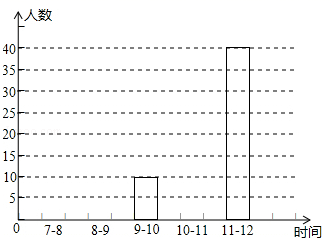

(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
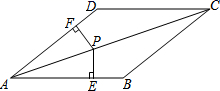
23.(10分)在四边形ABCD中,AB//CD,∠B=∠D.
(1)求证:四边形ABCD为平行四边形;
(2)若点P为对角线AC上的一点,PE⊥AB于E,PF⊥AD于F,且PE=PF,求证:四边形ABCD是菱形.
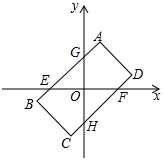
24.(12分)如图,四边形ABCD是以坐标原点O为对称中心的矩形,![]() ,该矩形的边与坐标轴分别交于点E、F、G、H.
,该矩形的边与坐标轴分别交于点E、F、G、H.
![]() 直接写出点C和点D的坐标;
直接写出点C和点D的坐标;
![]() 求直线CD的解析式;
求直线CD的解析式;
![]() 判断点
判断点![]() 在矩形ABCD的内部还是外部,并说明理由.
在矩形ABCD的内部还是外部,并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、D
4、A
5、D
6、B
7、D
8、A
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、1.
13、x≠1
14、x≥0
15、![]()
16、y=100t-500(15<t≤23)
三、解下列各题(本大题共8小题,共72分)
17、(1)证明见解析;(2)证明见解析.
18、(1)见解析;(2)![]() 是等腰三角形,见解析.
是等腰三角形,见解析.
19、解:(1)如图1、2,画一个即可:
(2)如图3、4,画一个即可:

20、1<x<4,数轴表示见解析.
21、(1)①详见解析;②60°.(1)IH=![]() FH;(3)EG1=AG1+CE1.
FH;(3)EG1=AG1+CE1.
22、(1)100人闯红灯(2)见解析;(3)众数为15人,中位数为20人
23、(1)证明见解析;(2)证明见解析.
24、(1)![]() .
.![]() ,(2)直线CD的解析式的解析式为:
,(2)直线CD的解析式的解析式为:![]() ;(3)点
;(3)点![]() 在矩形ABCD的外部.
在矩形ABCD的外部.
2023-2024学年浙江省江北区数学八年级第一学期期末调研模拟试题含答案: 这是一份2023-2024学年浙江省江北区数学八年级第一学期期末调研模拟试题含答案,共9页。试卷主要包含了下面是一名学生所做的4道练习题,下列命题,是真命题的是,下列二次根式中,可以与合并的是,如图,下面推理中,正确的是等内容,欢迎下载使用。
浙江省江北区2022-2023学年七年级数学第二学期期末教学质量检测试题含答案: 这是一份浙江省江北区2022-2023学年七年级数学第二学期期末教学质量检测试题含答案,共7页。试卷主要包含了在中,平分,,则的周长为等内容,欢迎下载使用。
浙江省宁波江北区四校联考2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案: 这是一份浙江省宁波江北区四校联考2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了已知,,则的结果为等内容,欢迎下载使用。












