


海南省定安县联考2022-2023学年数学七年级第二学期期末达标测试试题含答案
展开
这是一份海南省定安县联考2022-2023学年数学七年级第二学期期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列命题中,真命题是,下列命题是假命题的是,下列说法等内容,欢迎下载使用。
海南省定安县联考2022-2023学年数学七年级第二学期期末达标测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠DBC的度数是( ) A.36° B.45° C.54° D.72°2.将方程
A.36° B.45° C.54° D.72°2.将方程![]() 化成一元二次方程的一般形式,正确的是( ).A.
化成一元二次方程的一般形式,正确的是( ).A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.菱形的周长等于其高的8倍,则这个菱形的较大内角是( )A.30° B.120° C.150° D.135°4.在“爱我汾阳”演讲赛中,小明和其他6名选手参加决赛,他们决赛的成绩各不相同,小明想知道自己能否进入前4名,他除了知道自己成绩外还要知道这7名同学成绩的( )A.平均数 B.众数 C.中位数 D.方差5.二次根式
3.菱形的周长等于其高的8倍,则这个菱形的较大内角是( )A.30° B.120° C.150° D.135°4.在“爱我汾阳”演讲赛中,小明和其他6名选手参加决赛,他们决赛的成绩各不相同,小明想知道自己能否进入前4名,他除了知道自己成绩外还要知道这7名同学成绩的( )A.平均数 B.众数 C.中位数 D.方差5.二次根式![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.下列命题中,真命题是( )A.两条对角线相等的四边形是矩形;B.两条对角线互相垂直的四边形是菱形;C.两条对角线互相垂直且相等的四边形是正方形;D.两条对角线相等的梯形是等腰梯形7.下列命题是假命题的是( )A.直角三角形中,30°角所对的直角边等于斜边的一半B.三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等C.平行四边形是中心对称图形D.对角线相等的四边形是平行四边形8.下列说法:①对角线互相垂直的四边形是菱形;②矩形的对角线垂直且互相平分;③对角线相等的四边形是矩形;④对角线相等的菱形是正方形;⑤邻边相等的矩形是正方形.其中正确的是( )A.
6.下列命题中,真命题是( )A.两条对角线相等的四边形是矩形;B.两条对角线互相垂直的四边形是菱形;C.两条对角线互相垂直且相等的四边形是正方形;D.两条对角线相等的梯形是等腰梯形7.下列命题是假命题的是( )A.直角三角形中,30°角所对的直角边等于斜边的一半B.三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等C.平行四边形是中心对称图形D.对角线相等的四边形是平行四边形8.下列说法:①对角线互相垂直的四边形是菱形;②矩形的对角线垂直且互相平分;③对角线相等的四边形是矩形;④对角线相等的菱形是正方形;⑤邻边相等的矩形是正方形.其中正确的是( )A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个9.下列各二次根式中,可以与
个9.下列各二次根式中,可以与![]() 合并的是( )A.
合并的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
10.如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )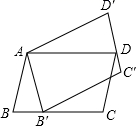 A.100° B.105° C.115° D.120°二、填空题(本大题共有6小题,每小题3分,共18分)11.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是_____.12.若
A.100° B.105° C.115° D.120°二、填空题(本大题共有6小题,每小题3分,共18分)11.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是_____.12.若![]() 是一个完全平方式,则
是一个完全平方式,则![]() 的值等于_________.13.已知点 A(2,a),B(3,b)在函数 y=1﹣x 的图象上,则 a 与 b 的大小关系是_____.14.分解因式:
的值等于_________.13.已知点 A(2,a),B(3,b)在函数 y=1﹣x 的图象上,则 a 与 b 的大小关系是_____.14.分解因式:![]() =________.15.如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,该图形的面积等于_____.
=________.15.如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,该图形的面积等于_____.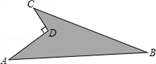 16.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.
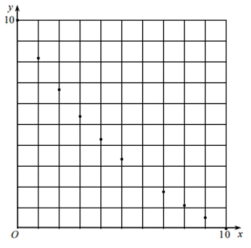
16.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.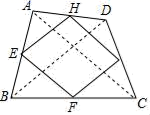 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,△ABC的三个顶点在正方形网格的格点上,网格中的每个小正方形的边长均为单位1.(1)求证:△ABC为直角三角形;(2)求点B到AC的距离.
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,△ABC的三个顶点在正方形网格的格点上,网格中的每个小正方形的边长均为单位1.(1)求证:△ABC为直角三角形;(2)求点B到AC的距离.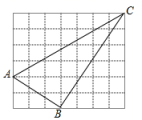 18.(8分)2018年5月,某城遭遇暴雨水灾,武警战士乘一冲锋舟从A地逆流而上,前往C地营救受困群众,途经B地时,由所携带的救生艇将B地受困群众运回A地,冲锋舟继续前进,到C地接到群众后立刻返回A地,途中曾与救生艇相遇,冲锋舟和救生艇距A地的距离y(千米)和冲锋舟出发后所用时间x(分)之间的函数图象如图所示,假设群众上下冲锋舟和救生艇的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.(1)冲锋舟从A地到C地的时间为 分钟,冲锋舟在静水中的速度为 千米/分,水流的速度为 千米/分.(2)冲锋舟将C地群众安全送到A地后,又立即去接应救生艇,已知救生艇与A地的距离y(千米)和冲锋舟出发后所用时间x(分钟)之间的函数关系式为y=kx+b,若冲锋舟在距离A地
18.(8分)2018年5月,某城遭遇暴雨水灾,武警战士乘一冲锋舟从A地逆流而上,前往C地营救受困群众,途经B地时,由所携带的救生艇将B地受困群众运回A地,冲锋舟继续前进,到C地接到群众后立刻返回A地,途中曾与救生艇相遇,冲锋舟和救生艇距A地的距离y(千米)和冲锋舟出发后所用时间x(分)之间的函数图象如图所示,假设群众上下冲锋舟和救生艇的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.(1)冲锋舟从A地到C地的时间为 分钟,冲锋舟在静水中的速度为 千米/分,水流的速度为 千米/分.(2)冲锋舟将C地群众安全送到A地后,又立即去接应救生艇,已知救生艇与A地的距离y(千米)和冲锋舟出发后所用时间x(分钟)之间的函数关系式为y=kx+b,若冲锋舟在距离A地![]() 千米处与救生艇第二次相遇,求k、b的值.
千米处与救生艇第二次相遇,求k、b的值.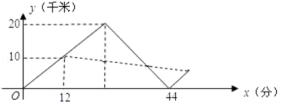 19.(8分)在平面直角坐标系中,一次函数
19.(8分)在平面直角坐标系中,一次函数![]() 的图象交
的图象交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,交直线
两点,交直线![]() 于
于![]() 。(1)求点
。(1)求点![]() 的坐标;(2)若
的坐标;(2)若![]() ,求
,求![]() 的值;(3)在(2)的条件下,
的值;(3)在(2)的条件下,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 点的坐标。
点的坐标。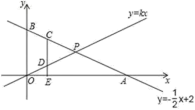 20.(8分)某校开展“涌读诗词经典,弘扬传统文化”诗词诵读活动,为了解八年级学生在这次活动中的诗词诵背情况,随机抽取了30名八年级学生,调查“一周诗词诵背数量”,调查结果如下表所示:一周诗词诵背数量(首)
20.(8分)某校开展“涌读诗词经典,弘扬传统文化”诗词诵读活动,为了解八年级学生在这次活动中的诗词诵背情况,随机抽取了30名八年级学生,调查“一周诗词诵背数量”,调查结果如下表所示:一周诗词诵背数量(首)![]()
![]()
![]()
![]()
![]()
![]() 人数(人)
人数(人)![]()
![]()
![]()
![]()
![]()
![]() (1)计算这
(1)计算这![]() 人平均每人一周诵背诗词多少首;(2)该校八年级共有6
人平均每人一周诵背诗词多少首;(2)该校八年级共有6![]() 名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词
名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词![]() 首以上(含6首)的学生有多少人. 21.(8分)如图①,在正方形ABCD中,
首以上(含6首)的学生有多少人. 21.(8分)如图①,在正方形ABCD中,![]() ,点E,F分别在BC、CD上,
,点E,F分别在BC、CD上,![]() ,试探究
,试探究![]() 面积的最小值。下面是小丽的探究过程:(1)延长EB至G,使
面积的最小值。下面是小丽的探究过程:(1)延长EB至G,使![]() ,连接AG,可以证明
,连接AG,可以证明![]() .请完成她的证明;(2)设
.请完成她的证明;(2)设![]() ,
,![]() ,
,![]() ①结合(1)中结论,通过计算得到
①结合(1)中结论,通过计算得到![]() 与x的部分对应值。请求出表格中a的值:(写出解答过程)x112345678911
与x的部分对应值。请求出表格中a的值:(写出解答过程)x112345678911![]() 118.186.675.384.293.33a1.761.111.531②利用上表和(1)中的结论通过描点、连线可以分别画出函数
118.186.675.384.293.33a1.761.111.531②利用上表和(1)中的结论通过描点、连线可以分别画出函数![]() 、
、![]() 的图像、请在图②中完善她的画图;③根据以上探究,估计
的图像、请在图②中完善她的画图;③根据以上探究,估计![]() 面积的最小值约为(结果估计到1.1)。
面积的最小值约为(结果估计到1.1)。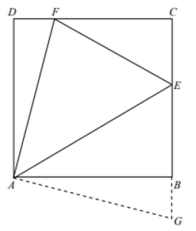
 图① 图② 22.(10分)如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
图① 图② 22.(10分)如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.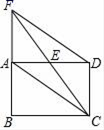 23.(10分)如图1,直线l1:y=﹣
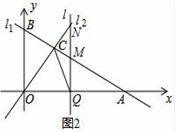
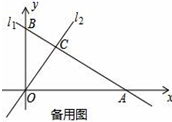
23.(10分)如图1,直线l1:y=﹣![]() x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.(1)求A,B两点的坐标;(2)求△BOC的面积;(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.①当OA=3MN时,求t的值;②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.(1)求A,B两点的坐标;(2)求△BOC的面积;(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.①当OA=3MN时,求t的值;②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.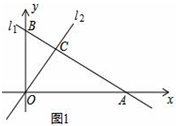
 24.(12分)如图,在
24.(12分)如图,在![]() 中,E点为AC的中点,且有
中,E点为AC的中点,且有![]() ,
,![]() ,
,![]() ,
,![]() 求DE的长.
求DE的长.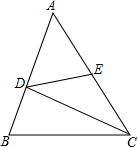 参考答案 一、选择题(每小题3分,共30分)1、A2、B3、C4、C5、B6、D7、D8、B9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、
参考答案 一、选择题(每小题3分,共30分)1、A2、B3、C4、C5、B6、D7、D8、B9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、![]() 13、a>b.14、
13、a>b.14、![]() 15、9616、AC⊥BD AC=BD AC⊥BD且AC=BD 三、解下列各题(本大题共8小题,共72分)17、 (1)见解析;(2)
15、9616、AC⊥BD AC=BD AC⊥BD且AC=BD 三、解下列各题(本大题共8小题,共72分)17、 (1)见解析;(2)![]() .18、(1)24,
.18、(1)24,![]() ,
,![]() (2)-
(2)-![]() ,119、(1)
,119、(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() .20、(1)5;(2)264021、(1)见解析;(2)①
.20、(1)5;(2)264021、(1)见解析;(2)①![]() ,②见解析;③41.4或41.5.22、(1)证明见解析;(2)BC=2CD,理由见解析.23、(1)A(6,0)B(0,3);(2)S△OBC=3;(3)①t=
,②见解析;③41.4或41.5.22、(1)证明见解析;(2)BC=2CD,理由见解析.23、(1)A(6,0)B(0,3);(2)S△OBC=3;(3)①t=![]() 或
或![]() ;②t=(6+2
;②t=(6+2![]() )s或(6﹣2
)s或(6﹣2![]() )s或2s或4s时,以O、Q、C、P为顶点的四边形构成菱形.24、DE=2.
)s或2s或4s时,以O、Q、C、P为顶点的四边形构成菱形.24、DE=2.
相关试卷
这是一份海南省定安县联考2023-2024学年数学九年级第一学期期末复习检测试题含答案,共8页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
这是一份海南省定安县2023-2024学年九上数学期末经典模拟试题含答案,共7页。试卷主要包含了已知抛物线的解析式为y=.,下列图标中,是中心对称图形的是等内容,欢迎下载使用。
这是一份2023-2024学年海南省定安县联考八上数学期末复习检测试题含答案,共6页。试卷主要包含了下列运算,正确的是,下列各组数是勾股数的是,已知,则的值是等内容,欢迎下载使用。









