浙江省温州市鹿城区2022-2023学年七下数学期末经典模拟试题含答案

浙江省温州市鹿城区2022-2023学年七下数学期末经典模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。

4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

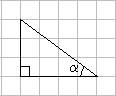
1．三角形在正方形网格纸中的位置如图所示，则的值是（）

A． B． C． D．

2．一次函数的图象大致是（   ）

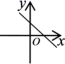A． B． C． D．

3．一个多边形的内角和与外角和相等，则这个多边形是（ ）

A．四边形 B．五边形 C．六边形 D．八边形

4．如图，有一高度为8m的灯塔AB，在灯光下，身高为1.6m的小亮从距离灯塔底端4.8m的点C处，沿BC方向前进3.2m到达点D处，那么他的影长（      ）

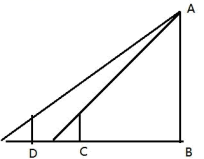
A．变长了0.8m B．变长了1.2m C．变短了0.8m D．变短了1.2m

5．若x＞y，则下列不等式中不一定成立的是（　　）

A．x﹣1＞y﹣1 B．2x＞2y C．x+1＞y+1 D．x2＞y2

6．如图，在平行四边形ABCD中，CE⊥AB，E为垂足．如果∠BCE＝28°，则∠D＝（　　）

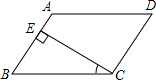
A．28° B．38° C．52° D．62°

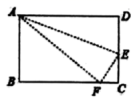
7．如图，在长方形中，，在上存在一点，沿直线把折叠，使点恰好落在边上的点处，若的面积为，那么折叠的的面积为（    ）

A．30 B．20 C． D．

8．如图，在▱ABCD中，AE⊥CD于点E，∠B＝65°，则∠DAE等于(　　)

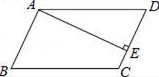
A．15° B．25° C．35° D．65°

9．已知点P（a，1）不在第一象限，则点Q（0，﹣a）在（　　）

A．x轴正半轴上 B．x轴负半轴上

C．y轴正半轴或原点上 D．y轴负半轴上

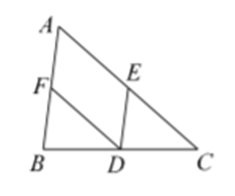
10．如图，在中，分别是边的中点．已知，则四边形的周长为(　　)

A． B． C． D．

11．如图，△ABC中，AB＝AC，AD是∠BAC的平分线．已知AB＝5，AD＝3，则BC的长为（　　）

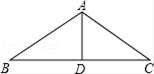
A．5 B．6 C．8 D．10

12．下列函数关系式：①y=-2x，②y＝−，③y=-2x2，④y=2，⑤y=2x-1．其中是一次函数的是（　　）

A．①⑤ B．①④⑤ C．②⑤ D．②④⑤

二、填空题（每题4分，满分20分，将答案填在答题纸上）

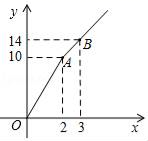
13．如图，购买“黄金1号”王米种子，所付款金额y元与购买量x（千克）之间的函数图象由线段OA和射线AB组成，则购买1千克“黄金1号”玉米种子需付款___元，购买4千克“黄金1号”玉米种子需___元．

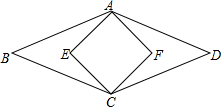
14．如图，B、E、F、D四点在同一条直线上，菱形ABCD的面积为120cm2，正方形AECF的面积为50cm2，则菱形的边长为_____cm．

15．某校生物小组7人到校外采集标本，其中2人每人采集到3件，3人每人采集到4件，2人每人采集到5件，则这个小组平均每人采集标本___________件.

16．已知点，在双曲线上，轴于点，轴于点，与交于点，是的中点，若的面积为4，则_______.

17．若数a使关于x的不等式组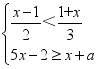有且只有四个整数解，且使关于y的方程＝2的解为非负数，则符合条件的所有整数a的和为_____．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）一个容器盛满纯药液，第一次倒出一部分纯药液后，用水加满；第二次又倒出同样多的药液，若此时容器内剩下的纯药液是，则每次倒出的液体是多少？

19．（5分）已知：关于x的一元二次方程ax2﹣2（a﹣1）x+a﹣2=0（a＞0）．

（1）求证：方程有两个不相等的实数根；

（2）设方程的两个实数根分别为x1，x2（其中x1＞x2）．若y是关于a的函数，且y=ax2•x1，求这个函数的表达式；

（3）将（2）中所得的函数的图象在直线a=2的左侧部分沿直线a=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象直接写出：当关于a的函数y=2a+b的图象与此图象有两个公共点时，b的取值范围是　　．

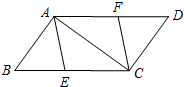
20．（8分）如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF

⑴求证：四边形AECF是平行四边形；

⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长．

21．（10分）（本小题满分12分）

直线y=x+6和x轴，y轴分别交于点E，F，点A是线段EF上一动点（不与点E重合），过点A作x轴垂线，垂足是点B，以AB为边向右作长方形ABCD，AB：BC=3：1．

（1）当点A与点F重合时（图1），求证：四边形ADBE是平行四边形，并求直线DE的表达式；

（2）当点A不与点F重合时（图2），四边形ADBE仍然是平行四边形？说明理由，此时你还能求出直线DE的表达式吗？若能，请你出来．

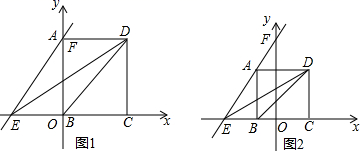
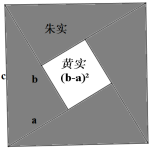
22．（10分）这个图案是3世纪三国时期的赵爽在注解《周髀算经》时给出的，人们称它为赵爽弦图．赵爽根据此图指出：四个全等的直角三角形（直角边分别为a、b，斜边为c）可以如图围成一个大正方形，中间的部分是一个小正方形．请用此图证明．

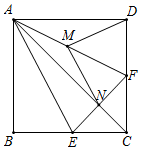
23．（12分）操作与证明：如图，把一个含角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AC、AE、其中AC与EF交于点N，取AF中点M，连接MD、MN．

求证：是等腰三角形；

在的条件下，请判断MD，MN的数量关系和位置关系，并给出证明．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、A

3、A

4、A

5、D

6、D

7、D

8、B

9、C

10、C

11、C

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、5    1．   

14、1．

15、4

16、2

17、1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、21

19、（1）见解析；（2）y=a﹣1（a＞0）；（1）﹣11＜b＜﹣2

20、⑴证明见解析

⑵5

21、（1）；（2）四边形ADBE仍然是平行四边形；.

22、证明见解析

23、（1）证明见解析；（2）