


清远市重点中学2022-2023学年数学七下期末学业质量监测试题含答案
展开这是一份清远市重点中学2022-2023学年数学七下期末学业质量监测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,分式方程的解为等内容,欢迎下载使用。
清远市重点中学2022-2023学年数学七下期末学业质量监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠BCE=28°,则∠D=( )
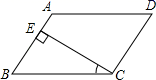
A.28° B.38° C.52° D.62°
2.下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
| 甲 | 乙 | 丙 | 丁 |
平均数 | 175 | 173 | 175 | 174 |
方差S2(cm2) | 3.5 | 3.5 | 12.5 | 15 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
3.对于函数![]() 有以下四个结论,其中正确的结论是( )
有以下四个结论,其中正确的结论是( )
A.函数图象必经过点![]() B.函数图象经过第一、二、三象限
B.函数图象经过第一、二、三象限
C.函数值y随x的增大而增大 D.当![]() 时,
时,![]()
4.在△ABC中,∠C=90°,AB=c,∠A=30°,则AC=( )
A.![]() c B.
c B.![]() c C.2c D.
c C.2c D.![]() c
c
5.下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.![]() ,
,![]() ,
,![]() C.3,4,6 D.4,5,6
C.3,4,6 D.4,5,6
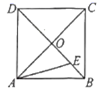
6.如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积是( )
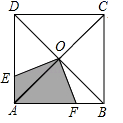
A.4 B.2 C.1 D.![]()
7.如图,直线![]()
![]() 与反比例函数
与反比例函数![]()
![]() 的图象交于
的图象交于![]() ,
,![]() 两点.若点
两点.若点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
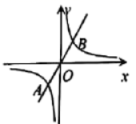
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.分式方程![]() 的解为( ).
的解为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,在三角形![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则点
,则点![]() 到
到![]() 的距离为( )
的距离为( )
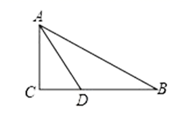
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若一次函数![]() 的图象经过第二、三、四象限,则a的取值范围是( )
的图象经过第二、三、四象限,则a的取值范围是( )
A.a≠3 B.a>0 C.a<3 D.0<a<3
11.如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
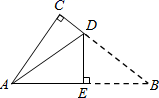
A.4 cm B.5 cm C.6 cm D.10 cm
12.为了迎接2022年的冬奥会,中小学都积极开展冰上运动,小明和小刚进行![]() 米短道速滑训练,他们的五次成绩如下表所示:
米短道速滑训练,他们的五次成绩如下表所示:
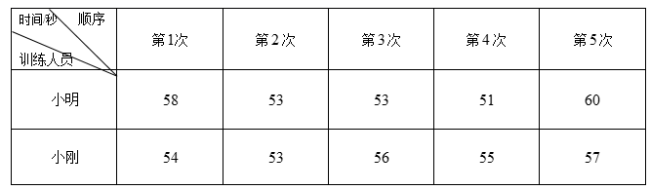
设两个人的五次成绩的平均数依次为![]() 、
、![]() ,方差依次为
,方差依次为![]() 、
、![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如图,在正方形ABCD中,对角线AC,BD交于点O,E为OB上的点,∠EAB=15°,若OE=![]() ,则AB的长为__.
,则AB的长为__.
14.如果一个n边形的内角和等于它的外角和的3倍,则n=______.
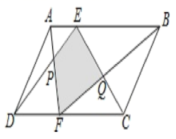
15.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若![]() ,
,![]() ,则阴影部分的面积为__________
,则阴影部分的面积为__________![]() .
.
16.![]() ___________
___________
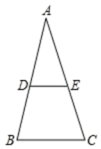
17.如图所示,D,E分别是△ABC的边AB,AC的中点,且BC=7,则DE=______.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
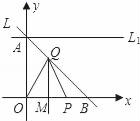
18.(5分)如图所示,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.
(1)直接写出直线L的解析式;
(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;
(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
19.(5分)(1)因式分解:2a3﹣8a2+8a;
(2)解不等式组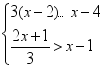 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
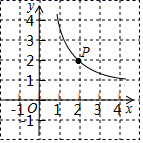
20.(8分)如图,反比例函数y=![]() (x>0)的图象过格点(网格线的交点)P.
(x>0)的图象过格点(网格线的交点)P.
(1)求反比例函数的解析式;
(2)在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点O,点P;
②矩形的面积等于k的值.
21.(10分)如图①,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形的外角平分线
交正方形的外角平分线![]() 于点
于点![]() 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
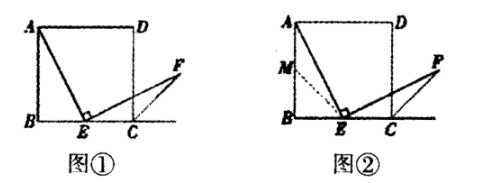
(1)探究1:小强看到图①后,很快发现![]() 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明![]() 就行了.随即小强写出了如下的证明过程:
就行了.随即小强写出了如下的证明过程:
证明:如图②,取AB的中点M,连接EM.
∵![]()
∴![]()
又∵![]()
∴![]()
∵点E、M分别为正方形的边BC和AB的中点,
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
又∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]()
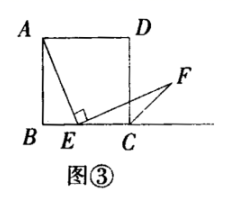
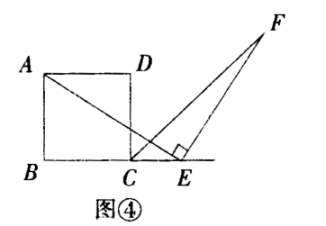
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
22.(10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
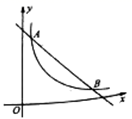
(1)求![]() ,
,![]() 的值;
的值;
(2)根据图象判断,当不等式![]() 成立时,
成立时,![]() 的取值范围是什么?
的取值范围是什么?
23.(12分)先化简,再求值![]() ,其中
,其中![]() .
.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、A
3、D
4、B
5、B
6、C
7、A
8、C
9、C
10、D
11、B
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、3![]()
14、1
15、40
16、-0.1
17、3.1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)y=1﹣x;(2)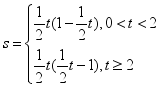 ,S有最大值
,S有最大值![]() ;(3)存在点C(1,1).
;(3)存在点C(1,1).
19、(1)![]() ;(2)1≤x<4,见解析
;(2)1≤x<4,见解析
20、(1)![]() ;(2)作图见解析.
;(2)作图见解析.
21、见解析
22、(1)![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]() .
.
23、x;2019.
相关试卷
这是一份2023-2024学年清远市重点中学八上数学期末学业质量监测试题含答案,共7页。试卷主要包含了如图,若,,,则的度数为,在平面直角坐标系中,已知点A等内容,欢迎下载使用。
这是一份陕西省重点中学2022-2023学年数学七下期末学业质量监测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,用反证法证明“”,应假设,关于的一元二次方程等内容,欢迎下载使用。
这是一份山东省重点中学2022-2023学年七下数学期末学业质量监测试题含答案,共7页。试卷主要包含了下列定理中,没有逆定理的是,若分式有意义,则x的取值范围是等内容,欢迎下载使用。












