


湖北省来凤县2022-2023学年七年级数学第二学期期末质量检测试题含答案
展开
这是一份湖北省来凤县2022-2023学年七年级数学第二学期期末质量检测试题含答案,共7页。试卷主要包含了下列二次根式中,最简二次根式是等内容,欢迎下载使用。
湖北省来凤县2022-2023学年七年级数学第二学期期末质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )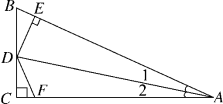 A.DE=DF B.BD=FD C.∠1=∠2 D.AB=AC2.下列图形中,既是轴对称图形,又是中心对称图形的是( )A.线段 B.直角三角形 C.等边三角形 D.平行四边形3.下列四个三角形,与左图中的三角形相似的是( )
A.DE=DF B.BD=FD C.∠1=∠2 D.AB=AC2.下列图形中,既是轴对称图形,又是中心对称图形的是( )A.线段 B.直角三角形 C.等边三角形 D.平行四边形3.下列四个三角形,与左图中的三角形相似的是( )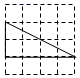 A.
A.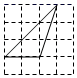 B.
B.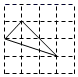 C.
C.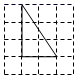 D.
D.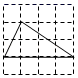 4.下列各组线段中,能够组成直角三角形的一组是( )A.1,2,3 B.2,3,4 C.4,5,6 D.1,
4.下列各组线段中,能够组成直角三角形的一组是( )A.1,2,3 B.2,3,4 C.4,5,6 D.1,![]() ,25.下列二次根式中,最简二次根式是( )A.
,25.下列二次根式中,最简二次根式是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是( )
6.如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是( )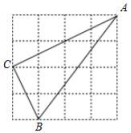 A.AB=5 B.∠C=90° C.AC=2
A.AB=5 B.∠C=90° C.AC=2![]() D.∠A=30°7.下列各数中,能使不等式x﹣3>0成立的是( )A.﹣3 B.5 C.3 D.28.一次函数
D.∠A=30°7.下列各数中,能使不等式x﹣3>0成立的是( )A.﹣3 B.5 C.3 D.28.一次函数![]() 的图象
的图象![]() 如图所示,将直线
如图所示,将直线![]() 向下平移若干个单位后得直线
向下平移若干个单位后得直线![]() ,
,![]() 的函数表达式为
的函数表达式为![]() .下列说法中错误的是( )
.下列说法中错误的是( )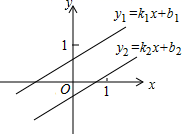 A.
A.![]() B.
B.![]() C.
C.![]() D.当
D.当![]() 时,
时,![]() 9.将直线
9.将直线![]() 向下平移2个单位,得到直线( )A.
向下平移2个单位,得到直线( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.下列各曲线中,不能表示y是x的函数是( )A.
10.下列各曲线中,不能表示y是x的函数是( )A.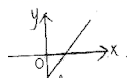 B.
B.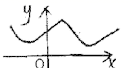 C.
C.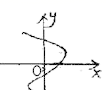 D.
D.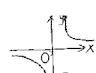 11.如图,在▱ABCD中,AC、BD相交于点O,点E是AB的中点.若OE=1cm,则AD的长是( )cm.
11.如图,在▱ABCD中,AC、BD相交于点O,点E是AB的中点.若OE=1cm,则AD的长是( )cm.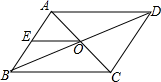 A.2 B.3 C.4 D.512.如图,有两个可以自由转动的转盘(每个转盘均被等分),同时转动这两个转盘,待转盘停止后,两个指针同时指在偶数上的概率是( )
A.2 B.3 C.4 D.512.如图,有两个可以自由转动的转盘(每个转盘均被等分),同时转动这两个转盘,待转盘停止后,两个指针同时指在偶数上的概率是( )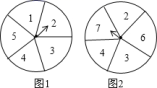 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,平行四边形
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,平行四边形![]() 的周长为
的周长为![]() ,对角线交于点
,对角线交于点![]() ,点
,点![]() 是边
是边![]() 的中点,已知
的中点,已知![]() ,则
,则![]() ______
______![]() .
.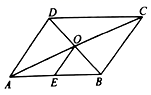 14.直线
14.直线![]() 与坐标轴围成的图形的面积为________.15.
与坐标轴围成的图形的面积为________.15.![]() 的整数部分是a,小数部分是b,则
的整数部分是a,小数部分是b,则![]() ________.16.从1、2、3、4这四个数中一次随机地取两个数,则其中一个数是另一个数两倍的概率是 .17.计算:
________.16.从1、2、3、4这四个数中一次随机地取两个数,则其中一个数是另一个数两倍的概率是 .17.计算:![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)学校准备从甲乙两位选手中选择一位参加汉字听写大赛,学校对两位选手的表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们的各项成绩(百分制)如表:选手表达能力阅读理解综合素质汉字听写甲85788573乙73808283如果表达能力、阅读理解、综合素质和汉字听写成绩按照2:1:3:4的比确定,请分别计算两名选手的平均成绩,从他们的成绩看,应选派谁? 19.(5分)《北京中小学语文学科教学21条改进意见》中的第三条指出:“在教学中重视对国学经典文化的学习,重视历史文化的熏陶,加强与革命传统教育的结合,使学生了解中华文化的悠久历史,增强民族文化自信和价值观自信,使语文教学成为涵养社会主义核心价值观的重要源泉之一”.为此,昌平区掀起了以“阅读经典作品,提升思维品质”为主题的读书活动热潮,在一个月的活动中随机调查了某校初二年级学生的周人均阅读时间的情况,整理并绘制了如下的统计图表:某校初二年级学生周人均阅读时间频数分布表周人均阅读时间x(小时)频数频率0≤x<2100.0252≤x<4600.1504≤x<6a0.2006≤x<81100.2758≤x<101000.25010≤x<1240b合计4001.000请根据以上信息,解答下列问题:(1)在频数分布表中a=______,b=______;(2)补全频数分布直方图;(3)若该校有1600名学生,根据调查数据请你估计,该校学生周人均阅读时间不少于6小时的学生大约有______人.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)学校准备从甲乙两位选手中选择一位参加汉字听写大赛,学校对两位选手的表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们的各项成绩(百分制)如表:选手表达能力阅读理解综合素质汉字听写甲85788573乙73808283如果表达能力、阅读理解、综合素质和汉字听写成绩按照2:1:3:4的比确定,请分别计算两名选手的平均成绩,从他们的成绩看,应选派谁? 19.(5分)《北京中小学语文学科教学21条改进意见》中的第三条指出:“在教学中重视对国学经典文化的学习,重视历史文化的熏陶,加强与革命传统教育的结合,使学生了解中华文化的悠久历史,增强民族文化自信和价值观自信,使语文教学成为涵养社会主义核心价值观的重要源泉之一”.为此,昌平区掀起了以“阅读经典作品,提升思维品质”为主题的读书活动热潮,在一个月的活动中随机调查了某校初二年级学生的周人均阅读时间的情况,整理并绘制了如下的统计图表:某校初二年级学生周人均阅读时间频数分布表周人均阅读时间x(小时)频数频率0≤x<2100.0252≤x<4600.1504≤x<6a0.2006≤x<81100.2758≤x<101000.25010≤x<1240b合计4001.000请根据以上信息,解答下列问题:(1)在频数分布表中a=______,b=______;(2)补全频数分布直方图;(3)若该校有1600名学生,根据调查数据请你估计,该校学生周人均阅读时间不少于6小时的学生大约有______人.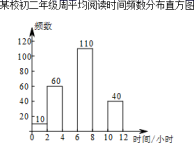 20.(8分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.(1)求一次函数y=kx+b的解析式;(2)若点D在y轴负半轴上,且满足S△COD═
20.(8分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.(1)求一次函数y=kx+b的解析式;(2)若点D在y轴负半轴上,且满足S△COD═![]() S△BOC,请直接写出点D的坐标.
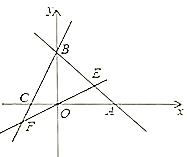
S△BOC,请直接写出点D的坐标.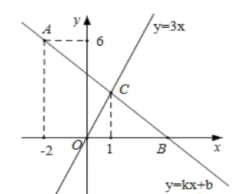 21.(10分)直线
21.(10分)直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线交
的直线交![]() 轴负半轴于
轴负半轴于![]() ,且
,且![]() .
.
![]() 求点
求点![]() 坐标.
坐标.![]() 求直线
求直线![]() 的解析式.
的解析式.![]() 直线
直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() . 22.(10分)如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4(1)求证:△OBE是等腰三角形;(2)求E点的坐标;(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
. 22.(10分)如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4(1)求证:△OBE是等腰三角形;(2)求E点的坐标;(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.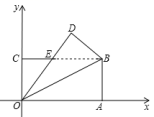 23.(12分)如图1,在等边△ABC中,AB=BC=AC=8cm,现有两个动点E,P分别从点A和点B同时出发,其中点E以1cm/秒的速度沿AB向终点B运动;点P以2cm/秒的速度沿射线BC运动.过点E作EF∥BC交AC于点F,连接EP,FP.设动点运动时间为t秒(0<t≤8).(1)当点P在线段BC上运动时,t为何值,四边形PCFE是平行四边形?请说明理由;(2)设△EBP的面积为y(cm2),求y与t之间的函数关系式;(3)当点P在射线BC上运动时,是否存在某一时刻t,使点C在PF的中垂线上?若存在,请直接给出此时t的值(无需证明),若不存在,请说明理由.
23.(12分)如图1,在等边△ABC中,AB=BC=AC=8cm,现有两个动点E,P分别从点A和点B同时出发,其中点E以1cm/秒的速度沿AB向终点B运动;点P以2cm/秒的速度沿射线BC运动.过点E作EF∥BC交AC于点F,连接EP,FP.设动点运动时间为t秒(0<t≤8).(1)当点P在线段BC上运动时,t为何值,四边形PCFE是平行四边形?请说明理由;(2)设△EBP的面积为y(cm2),求y与t之间的函数关系式;(3)当点P在射线BC上运动时,是否存在某一时刻t,使点C在PF的中垂线上?若存在,请直接给出此时t的值(无需证明),若不存在,请说明理由.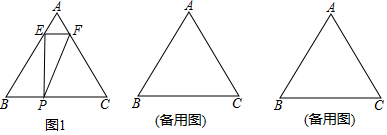 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、B4、D5、B6、D7、B8、B9、A10、C11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、115、216、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、B4、D5、B6、D7、B8、B9、A10、C11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、115、216、![]() 17、2. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、应派乙去19、(1)80,0.100;(2)见解析;(3)1.20、(1)y=−x+4;(2)(0,−6)21、(1)(0,6);(2)y=3x+6;(3)证明见详解22、(1)见解析; (2)(3,4); (3)(
17、2. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、应派乙去19、(1)80,0.100;(2)见解析;(3)1.20、(1)y=−x+4;(2)(0,−6)21、(1)(0,6);(2)y=3x+6;(3)证明见详解22、(1)见解析; (2)(3,4); (3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).23、(1)t=
).23、(1)t=![]() ;(2)y-
;(2)y-![]() t2+4
t2+4![]() t(0<t≤8);(3)t=
t(0<t≤8);(3)t=![]() 时,点C在PF的中垂线上.
时,点C在PF的中垂线上.
相关试卷
这是一份湖北省来凤县2023-2024学年数学九年级第一学期期末教学质量检测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,图中三视图所对应的直观图是,若一次函数y=ax+b等内容,欢迎下载使用。
这是一份2023-2024学年湖北省恩施土家族苗族自治州来凤县数学八上期末质量检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列分解因式正确的是,下列各式中,正确的有,平面直角坐标系中,点等内容,欢迎下载使用。
这是一份湖北省恩施土家族苗族自治州来凤县2022-2023学年七年级数学第二学期期末统考模拟试题含答案,共8页。试卷主要包含了点P,下列等式正确的是等内容,欢迎下载使用。









