湖南省永州市新田县2022-2023学年七下数学期末达标检测试题含答案

湖南省永州市新田县2022-2023学年七下数学期末达标检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。

4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．关于正比例函数y＝﹣3x，下列结论正确的是（　　）

A．图象不经过原点 B．y随x的增大而增大

C．图象经过第二、四象限 D．当x＝时，y＝1

2．关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根，则k的取值范围是（ ）

A．k＞﹣1 B．k＞﹣1且k≠0 C．k≠0 D．k≥﹣1

3．小颖同学准备用26元买笔和笔记本，已知一支笔2元，一本笔记本3元，他买了5本笔记本，最多还能买多少支笔？设他还能买支笔，则列出的不等式为（    ）

A． B．

C． D．

4．下列说法正确的是（　　）

A．若两个向量相等则起点相同，终点相同

B．零向量只有大小，没有方向

C．如果四边形ABCD是平行四边形，那么＝

D．在平行四边形ABCD中，﹣＝

5．如果点A（﹣2，a）在函数yx+3的图象上，那么a的值等于（　　）

A．﹣7 B．3 C．﹣1 D．4

6．函数中，自变量x的取值范围是（ ）

A． B． C． D．

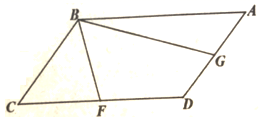
7．如图，在平行四边形ABCD中，F，G分别为CD，AD的中点，BF=2，BG=3，，则BC的长度为（  ）

A． B． C．2.5 D．

8．下列化简正确的是（   ）

A． B． C． D．

9．两组数据：98,99,99,100和98.5,99,99,99.5，则关于以下统计量说法不正确的是(　　)

A．平均数相等

B．中位数相等

C．众数相等

D．方差相等

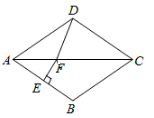
10．如图，在菱形中，，的垂直平分线交对角线于点,为垂足，连结，则等于（    ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．一个n边形的内角和是720°，则n＝_____．

12．将二次根式化为最简二次根式的结果是________________

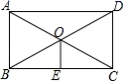
13．如图，矩形ABCD 的对角线AC，BD的交点为O，点E为BC边的中点，，如果OE=2，那么对角线BD的长为______．

14．观察下列各式

==2；==3；==4；==5……请你找出其中规律，并将第n（n≥1）个等式写出来____________。

15．一组数据：，计算其方差的结果为__________．

16．对于任意非零实数a，b，定义“☆”运算为：a☆b＝，若（x+1）☆x+（x+2）☆（x+1）+（x+3）☆（x+2）+…+（x+2018）☆（x+2017）＝，则x＝_____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）解不等式组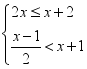：，并把不等式组的解集在数轴上表示出来.

18．（8分）先化简，再求值：（）（x2－4），其中x=．

19．（8分）某商店计划购进A、B两种型号的电动自行车共30辆，其中A型电动自行车不少于20辆，A、B两种型号电动自行车的进货单价分别为2500元、3000元，售价分别为2800元、3500元，设该商店计划购进A型电动自行车m辆，两种型号的电动自行车全部销售后可获利润y元．

（1）求出y与m之间的函数关系式；

（2）该商店如何进货才能获得最大利润？此时最大利润是多少元？

20．（8分）    解不等式组：，并求出它的整数解的和．

21．（8分）解不等式组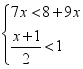：，并写出它的所有整数解．

22．（10分）随着人们环保意识的增强，越来越多的人选择低碳出行，各种品牌的山地自行车相继投放市场.顺风车行五月份型车的销售总利润为元，型车的销售总利润为元.且型车的销售数量是型车的倍，已知销售型车比型车每辆可多获利元.

（1）求每辆型车和型车的销售利润；

（2）若该车行计划一次购进两种型号的自行车共台且全部售出，其中型车的进货数量不超过型车的倍，则该车行购进型车、型车各多少辆，才能使销售总利润最大？最大销售总利润是多少？

23．（10分）我省某苹果基地销售优质苹果，该基地对需要送货且购买量在2 000 kg～5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案)：

方案A：每千克5.8元，由基地免费送货；

方案B：每千克5元，客户需支付运费2 000元．

(1)请分别写出按方案A，方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式；

(2)求购买量x在什么范围时，选用方案A比方案B付款少；

(3)某水果批发商计划用20 000元，选用这两种方案中的一种，购买尽可能多的这种苹果，请直接写出他应选择哪种方案．

24．（12分）图①，图②都是4×6的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在图①，图②中已画出线段AB，且点A，B均在格点上．

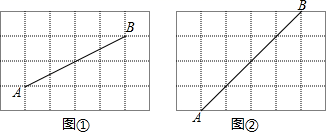
（1）在图①中以AB为对角线画出一个矩形，使矩形的另外两个顶点也在格点上，且所画的矩形不是正方形；

（2）在图②中以AB为对角线画出一个菱形，使菱形的另外两个顶点也在格点上，且所画的菱形不是正方形；

（3）图①中所画的矩形的面积为　   　；图②中所画的菱形的周长为　   　．

参考答案

一、选择题(每小题3分,共30分)

1、C

2、B

3、A

4、C

5、D

6、B

7、A

8、A

9、D

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、4

13、1

14、

15、

16、﹣1

三、解下列各题(本大题共8小题，共72分)

17、；数轴表示见解析.

18、

19、（1）＝﹣200+15000（20≤m＜30）；（2）    购进A型电动自行车20辆，购进B型10辆，最大利润是11000元．

20、﹣1＜x≤2，1.

21、解集为-4＜x＜2，不等式组的整数解是：﹣3，﹣2，﹣1、1．

22、（1）每辆A型车的利润为1元，每辆B型车的利润为2元．（2）商店购进34台A型车和66台B型车，才能使销售总利润最大，最大利润是3元．

23、 (1)方案A：y＝5.8x；方案B：y＝5x＋2 000(2)选用方案A比方案B付款少(3) B

24、（1）见解析；（2）见解析；（3）8，4．