


湖南省张家界市桑植县2022-2023学年数学七下期末质量跟踪监视模拟试题含答案
展开
这是一份湖南省张家界市桑植县2022-2023学年数学七下期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了下列命题是真命题的是等内容,欢迎下载使用。
湖南省张家界市桑植县2022-2023学年数学七下期末质量跟踪监视模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列调查中,最适合采用全面调查(普查)方式的是( )A.对无锡市空气质量情况的调查 B.对某校七年级(![]() )班学生视力情况的调查C.对某批次手机屏使用寿命的调查 D.对全国中学生每天体育锻炼所用时间的调查2.下列调查方式中适合的是( )A.要了解一批节能灯的使用寿命,采用普查方式B.调查你所在班级同学的身高,采用抽样调查方式C.环保部门调查长江某段水域的水质情况,采用抽样调查方式D.调查全市中学生每天的就寝时间,采用普查方式3.以下是某市自来水价格调整表(部分):(单位:元/立方米)用水类别现行水价拟调整水价一、居民生活用水0.72 1、一户一表 第一阶梯:月用水量0~30立方米/户 0.82第二阶梯:月用水量超过30立方米/户部分 1.23则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是( )A.
)班学生视力情况的调查C.对某批次手机屏使用寿命的调查 D.对全国中学生每天体育锻炼所用时间的调查2.下列调查方式中适合的是( )A.要了解一批节能灯的使用寿命,采用普查方式B.调查你所在班级同学的身高,采用抽样调查方式C.环保部门调查长江某段水域的水质情况,采用抽样调查方式D.调查全市中学生每天的就寝时间,采用普查方式3.以下是某市自来水价格调整表(部分):(单位:元/立方米)用水类别现行水价拟调整水价一、居民生活用水0.72 1、一户一表 第一阶梯:月用水量0~30立方米/户 0.82第二阶梯:月用水量超过30立方米/户部分 1.23则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是( )A.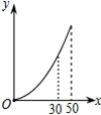 B.
B.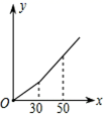 C.
C.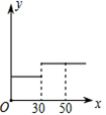 D.
D. 4.下列命题是真命题的是( )A.对角线互相平分的四边形是平行四边形 B.对角线相等的四边形是矩形C.对角线互相垂直且相等的四边形是正方形 D.对角线互相垂直的四边形是菱形5.如图,矩形
4.下列命题是真命题的是( )A.对角线互相平分的四边形是平行四边形 B.对角线相等的四边形是矩形C.对角线互相垂直且相等的四边形是正方形 D.对角线互相垂直的四边形是菱形5.如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 的长为( )
的长为( )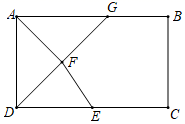 A.3 B.4 C.5 D.66.若一个正方形的面积为(ɑ+1)(ɑ+2)+
A.3 B.4 C.5 D.66.若一个正方形的面积为(ɑ+1)(ɑ+2)+![]() ,则该正方形的边长为( )A.
,则该正方形的边长为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,在正方形
7.如图,在正方形![]() 中,点
中,点![]() 是边
是边![]() 上的一个动点(不与点
上的一个动点(不与点![]() ,
,![]() 重合),
重合),![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() 若
若![]() ,则
,则![]() 的值为( )
的值为( )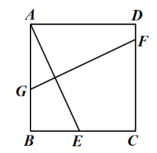 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.若二次根式
8.若二次根式![]() 有意义,则x能取的最小整数值是( )A.x=0 B.x=1 C.x=2 D.x=39.式子
有意义,则x能取的最小整数值是( )A.x=0 B.x=1 C.x=2 D.x=39.式子![]() 有意义,则实数a的取值范围是( )A.a≥-1 B.a≠2 C.a≥-1且a≠2 D.a>210.甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
有意义,则实数a的取值范围是( )A.a≥-1 B.a≠2 C.a≥-1且a≠2 D.a>210.甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( ) 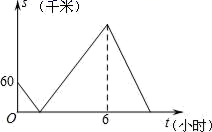 A.货车的速度是60千米/小时B.离开出发地后,两车第一次相遇时,距离出发地150千米C.货车从出发地到终点共用时7小时D.客车到达终点时,两车相距180千米11.若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )A.4 B.3 C.5 D.612.如图,在△ABC中,点D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,下列说法错误的是( )
A.货车的速度是60千米/小时B.离开出发地后,两车第一次相遇时,距离出发地150千米C.货车从出发地到终点共用时7小时D.客车到达终点时,两车相距180千米11.若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )A.4 B.3 C.5 D.612.如图,在△ABC中,点D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,下列说法错误的是( )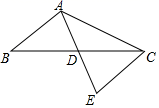 A.△ABD≌△ECDB.连接BE,四边形ABEC为平行四边形C.DA=DED.CE=CA二、填空题(每题4分,满分20分,将答案填在答题纸上)13.已知关于x的分式方程
A.△ABD≌△ECDB.连接BE,四边形ABEC为平行四边形C.DA=DED.CE=CA二、填空题(每题4分,满分20分,将答案填在答题纸上)13.已知关于x的分式方程![]() 有一个正数解,则k的取值范围为________.14.已知
有一个正数解,则k的取值范围为________.14.已知![]() ,则
,则![]() 的值等于________. 15.如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件:______,使四边形ABCD为平行四边形(不添加任何辅助线).
的值等于________. 15.如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件:______,使四边形ABCD为平行四边形(不添加任何辅助线). 16.若一个三角形的三边的比为3:4:5,则这个三角形的三边上的高之比为__________.17.如图,正方形 ABCD 的顶点 C, A 分别在 x 轴, y 轴上, BC 是菱形 BDCE 的对角线.若 BC 6, BD 5, 则点 D 的坐标是_____.
16.若一个三角形的三边的比为3:4:5,则这个三角形的三边上的高之比为__________.17.如图,正方形 ABCD 的顶点 C, A 分别在 x 轴, y 轴上, BC 是菱形 BDCE 的对角线.若 BC 6, BD 5, 则点 D 的坐标是_____. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知点
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .(1)如图1,若
.(1)如图1,若![]() ,求证:
,求证:![]() ;(2)如图2,若
;(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;(3)如图3,若
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.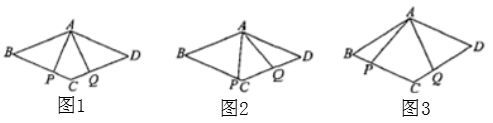 19.(5分)如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连接PO并延长交BC于点Q,设运动时间为t (0<t<5).(1)当t为何值时,四边形ABQP是平行四边形?(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.
19.(5分)如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连接PO并延长交BC于点Q,设运动时间为t (0<t<5).(1)当t为何值时,四边形ABQP是平行四边形?(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.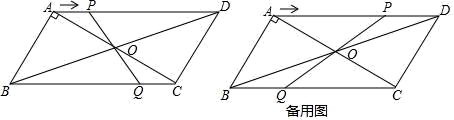 20.(8分)如图,点A(1,0),点B在y轴正半轴上,直线AB与直线l:y=
20.(8分)如图,点A(1,0),点B在y轴正半轴上,直线AB与直线l:y=![]() 相交于点C,直线l与x轴交于点D,AB=
相交于点C,直线l与x轴交于点D,AB=![]() .(1)求点D坐标;(2)求直线AB的函数解析式;(3)求△ADC的面积.
.(1)求点D坐标;(2)求直线AB的函数解析式;(3)求△ADC的面积.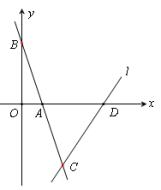 21.(10分)如图:
21.(10分)如图:![]() 、
、![]() 是锐角
是锐角![]() 的两条高,
的两条高,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,若EF=6,
的中点,若EF=6,![]() .
.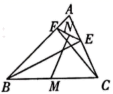 (1)证明:
(1)证明:![]() ;(2)判断
;(2)判断![]() 与
与![]() 的位置关系,并证明你的结论;(3)求
的位置关系,并证明你的结论;(3)求![]() 的长. 22.(10分)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.(1)正方体的棱长为 cm;(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
的长. 22.(10分)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.(1)正方体的棱长为 cm;(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.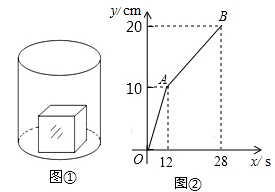 23.(12分)解不等式组:
23.(12分)解不等式组: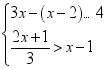 ,并将解集在数轴上表示出来,且写出它的整数解. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、B4、A5、C6、B7、C8、B9、C10、C11、A12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、k<6且k≠1 14、315、AD=BC.16、20:15:1.17、
,并将解集在数轴上表示出来,且写出它的整数解. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、B4、A5、C6、B7、C8、B9、C10、C11、A12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、k<6且k≠1 14、315、AD=BC.16、20:15:1.17、![]() . 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)(1)中的结论还成立,证明见解析;(3)四边形
. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)(1)中的结论还成立,证明见解析;(3)四边形![]() 的面积为
的面积为![]() .19、(1)当t=
.19、(1)当t=![]() 时,四边形ABQP是平行四边形(2)y=
时,四边形ABQP是平行四边形(2)y=![]() t+3(3)存在,当t=
t+3(3)存在,当t=![]() 时,点O在线段AP的垂直平分线上20、(1)点D坐标为(4,0);(2)s=﹣1x+1;(1)
时,点O在线段AP的垂直平分线上20、(1)点D坐标为(4,0);(2)s=﹣1x+1;(1)![]() 21、(1)证明见解析;(2)MN垂直平分EF,证明见解析;(3)MN=
21、(1)证明见解析;(2)MN垂直平分EF,证明见解析;(3)MN=![]() .22、(1)10;(2)y=
.22、(1)10;(2)y=![]() x+
x+![]() (12≤x≤28);(3)4 s.23、不等式组的解集为
(12≤x≤28);(3)4 s.23、不等式组的解集为![]() ;整数解为
;整数解为![]() .
.
相关试卷
这是一份2023-2024学年湖南省张家界市桑植县九上数学期末质量跟踪监视试题含答案,共6页。试卷主要包含了已知二次函数y=x2﹣6x+m,下列方程中不是一元二次方程的是等内容,欢迎下载使用。
这是一份湖南省长沙市明德中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列函数中,是反比例函数的为等内容,欢迎下载使用。
这是一份湖南省雅礼教育集团2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了下列运算,正确的是,一次统计八,在实数范围内,下列判断正确的是等内容,欢迎下载使用。








