湖南省长沙市明德教育集团2022-2023学年数学七下期末统考试题含答案

这是一份湖南省长沙市明德教育集团2022-2023学年数学七下期末统考试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，若分式的值为零，则的值为等内容，欢迎下载使用。
湖南省长沙市明德教育集团2022-2023学年数学七下期末统考试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。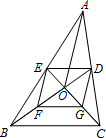 一、选择题(每小题3分,共30分)1．已知一组数据：1，2，8，，7，它们的平均数是1．则这组数据的中位数是（    ）A．7 B．1 C．5 D．42．已知y关于x成正比例，且当时，，则当时，y的值为A．3 B． C．12 D．3．为了解我市参加中考的15 000名学生的视力情况，抽查了1 000名学生的视力进行统计分析，下面四个判断正确的是（ ）A．15000名学生是总体B．1000名学生的视力是总体的一个样本C．每名学生是总体的一个个体D．以上调查是普查4．下列函数中是一次函数的为(　　)A．y＝8x2 B．y＝x＋1 C．y＝ D．y＝5．如图，在△中，、是△的中线，与相交于点，点、分别是、的中点，连结.若＝6cm，＝8cm，则四边形DEFG的周长是（ ）A．14cm B．18 cmC．24cm D．28cm6．矩形一个角的平分线分矩形一边为2cm和3cm两部分，则这个矩形的面积为（    ）A．10cm2 B．15cm2 C．12cm2 D．10cm2或15cm27．若分式的值为零，则的值为(    )A． B． C． D．8．正比例函数的图象经过点，，当时，，则的取值范围是（    ）A． B． C． D．9．已知一个等腰三角形的两边长分别是2和4，则该等腰三角形的周长为（ ）A．8或10 B．8 C．10 D．6或1210．在平面直角坐标系中，点P(－2，＋1)所在的象限是（ ）A．第一象限 B．第二象限 C．第三象限 D．第四象限二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为_____cm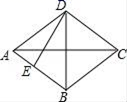．12．一组数据5，7，2，5，6的中位数是_____．13．某汽车生产厂对其生产的A型汽车进行油耗试验，试验中汽车为匀速行驶汽在行驶过程中，油箱的余油量y（升）与行驶时间t（小时）之间的关系如下表：t（小时）1123y（升）111928476由表格中y与t的关系可知，当汽车行驶________小时，油箱的余油量为1．14．将直线y＝﹣4x+3向下平移4个单位，得到的直线解析式是_____．15．已知P1（1，y1），P2（2，y2）是正比例函数的图象上的两点，则y1       y2（填“＞”或“＜”或“=”）．16．分式方程的解是_____．三、解下列各题(本大题共8小题，共72分)17．（8分）计算（+1）（-1）+÷−.   18．（8分）如图，在△ABC中，∠C=90°， ∠B=30°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，又分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D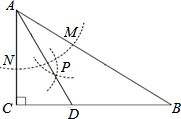．求证：（1）点D在AB的中垂线上．（2）当CD=2时，求△ABC的面积．   19．（8分）本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面两个统计图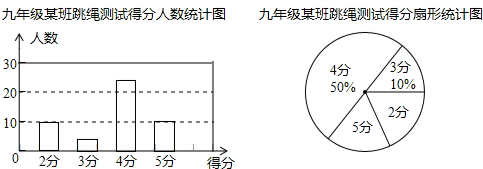．根据统计图解答下列问题：（1）本次测试的学生中，得4分的学生有多少人？（2）本次测试的平均分是多少分？（3）通过一段时间的训练，体育组对该班学生的跳绳项目进行了第二次测试，测得成绩的最低分为3分．且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中得4分、5分的学生各有多少人？   20．（8分）如图,已知平面直角坐标系中,、,现将线段绕点顺时针旋转得到点,连接.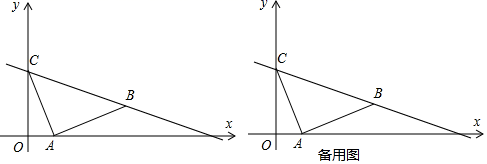(1)求出直线的解析式；(2)若动点从点出发,沿线段以每分钟个单位的速度运动,过作交轴于,连接.设运动时间为分钟,当四边形为平行四边形时,求的值.(3)为直线上一点,在坐标平面内是否存在一点,使得以、、、为顶点的四边形为菱形,若存在,求出此时的坐标；若不存在,请说明理由.   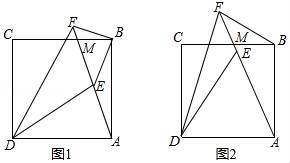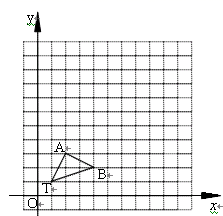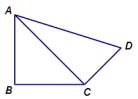21．（8分）如图，点M是正方形ABCD的边BC上一点，连接AM，点E是线段AM上一点，∠CDE的平分线交AM延长线于点F．(1)如图1，若点E为线段AM的中点，BM：CM＝1：2，BE＝，求AB的长；(2)如图2，若DA＝DE，求证：BF+DF＝AF．   22．（10分）如图，在12×12的正方形网格中，△TAB 的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）．（1）以点T（1，1）为位似中心，按比例尺（TA′∶TA）3∶1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′．画出△TA′B′，并写出点A′、B′的坐标；（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标．   23．（10分）如图，在四边形ABCD中，AB=BC=3，CD=，DA=5，∠B=90°，求∠BCD的度数   24．（12分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，请按要求完成下列步骤：（1）画出将△ABC向上平移3个单位后得到的△A1B1C1；（2）画出将△A1B1C1绕点C1按顺时针方向旋转90°后所得到的△A2B2C1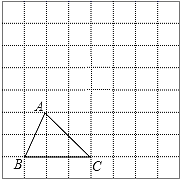．   参考答案 一、选择题(每小题3分,共30分)1、A2、B3、B4、B5、A6、D7、C8、C9、C10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、4.112、113、12.214、y＝﹣4x﹣115、＜.16、 三、解下列各题(本大题共8小题，共72分)17、1+18、（1）见解析；（2）619、（1）25人（2）37分（3）第二次测试中得4分的学生有15人、得5分的学生有30人．20、（1）；（2）t=s时，四边形ABMN是平行四边形；（3）存在，点Q坐标为：或或或.21、 (1)AB＝2；(1)证明见解析.22、（1）A′坐标为（4，7），B′坐标为（10，4）；（2）点C′的坐标为(3a－2，3b－2 ) ．23、135°.24、（1）作图见解析；（2）作图见解析.