


湖南省株洲市荷塘区第五中学2022-2023学年七下数学期末联考试题含答案
展开
这是一份湖南省株洲市荷塘区第五中学2022-2023学年七下数学期末联考试题含答案,共6页。试卷主要包含了若是关于,的二元一次方程,则,将点A,下列计算正确的是,直线等内容,欢迎下载使用。
湖南省株洲市荷塘区第五中学2022-2023学年七下数学期末联考试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算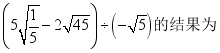 ( )A.7 B.-5 C.5 D.-72.如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(3,0)、(-2,0),点D在y轴正半轴上,则点C的坐标为( )
( )A.7 B.-5 C.5 D.-72.如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(3,0)、(-2,0),点D在y轴正半轴上,则点C的坐标为( )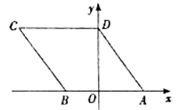 A.(-3,4). B.(-4,3). C.(-5,3). D.(-5,4).3.将一张矩形纸片
A.(-3,4). B.(-4,3). C.(-5,3). D.(-5,4).3.将一张矩形纸片![]() 沿一组对边
沿一组对边![]() 和
和![]() 的中点连线
的中点连线![]() 对折,对折后所得矩形恰好与原矩形相似,若原矩形纸片的边
对折,对折后所得矩形恰好与原矩形相似,若原矩形纸片的边![]() ,则
,则![]() 的长为( )A.
的长为( )A.![]() B.
B.![]() C.
C.![]() D.24.若
D.24.若![]() 是关于
是关于![]() ,
,![]() 的二元一次方程,则( )A.
的二元一次方程,则( )A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]() 5.将点A(1,﹣1)向上平移2个单位后,再向左平移3个单位,得到点B,则点B的坐标为( )A.(2,1) B.(﹣2,﹣1) C.(﹣2,1) D.(2,﹣1)6.图中的两个三角形是位似图形,它们的位似中心是( )
5.将点A(1,﹣1)向上平移2个单位后,再向左平移3个单位,得到点B,则点B的坐标为( )A.(2,1) B.(﹣2,﹣1) C.(﹣2,1) D.(2,﹣1)6.图中的两个三角形是位似图形,它们的位似中心是( )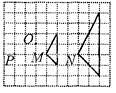 A.点P B.点DC.点M D.点N7.下列计算正确的是( )A.
A.点P B.点DC.点M D.点N7.下列计算正确的是( )A.![]() B.
B.![]() C.
C.![]()
![]() D.
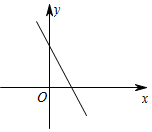
D.![]() 8.直线:
8.直线:![]() 为常数
为常数![]() 的图象如图,化简:
的图象如图,化简:![]()
![]()
 A.3 B.
A.3 B.![]() C.
C.![]() D.59.如图,矩形
D.59.如图,矩形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,如果
,如果![]() ,那么
,那么![]() 度数是( )
度数是( )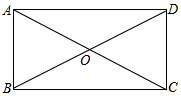 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.对于任意不相等的两个实数
10.对于任意不相等的两个实数![]() ,
,![]() ,定义运算如下:
,定义运算如下:![]() .如果
.如果![]() ,那么
,那么![]() 的值为( )A.
的值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.化简
11.化简![]() 的结果是( ).A.
的结果是( ).A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为()
12.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为()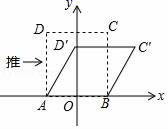 A.(
A.(![]() ,1) B.(2,1)C.(2,
,1) B.(2,1)C.(2,![]() ) D.(1,
) D.(1,![]() )二、填空题(每题4分,满分20分,将答案填在答题纸上)13.在反比例函数
)二、填空题(每题4分,满分20分,将答案填在答题纸上)13.在反比例函数![]() 图象的毎一支曲线上,y都随x的增大而减小,则k的取值范围是__________.14.已知x+y=
图象的毎一支曲线上,y都随x的增大而减小,则k的取值范围是__________.14.已知x+y=![]() ,xy=
,xy=![]() ,则x2y+xy2的值为____.15.分解因式:
,则x2y+xy2的值为____.15.分解因式:![]() ___.16.当x=4时,二次根式
___.16.当x=4时,二次根式![]() 的值为______.17.某校四个植树小队,在植树节这天种下柏树的棵数分别为10,x,10,8,若这组数据的中位数和平均数相等,那么x=_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.(1)若AB=8,AC=4,求DE的长;(2)求证:AB-AC=2DM.
的值为______.17.某校四个植树小队,在植树节这天种下柏树的棵数分别为10,x,10,8,若这组数据的中位数和平均数相等,那么x=_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.(1)若AB=8,AC=4,求DE的长;(2)求证:AB-AC=2DM.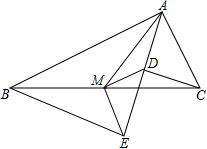 19.(5分)如图,四边形
19.(5分)如图,四边形![]() 的对角线
的对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 、
、![]() 是
是![]() 上两点,
上两点,![]() ,
,![]() ,
,![]() .
.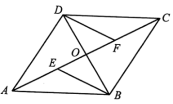 (1)求证:四边形
(1)求证:四边形![]() 是平行四边形.(2)当
是平行四边形.(2)当![]() 平分
平分![]() 时,求证:
时,求证:![]() . 20.(8分)已知x=2﹣
. 20.(8分)已知x=2﹣![]() ,y=2+
,y=2+![]() ,求下列代数式的值(1)x2+2xy+y2;(2)
,求下列代数式的值(1)x2+2xy+y2;(2)![]()
![]() 21.(10分)我们可用
21.(10分)我们可用![]() 表示以
表示以![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示为
,可表示为![]() ,且
,且![]() ,
,![]() ,定义:若存在实数
,定义:若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,例如:
的不动点,例如:![]() ,令
,令![]() ,得
,得![]() ,那么
,那么![]() 的不动点是1.(1)已知函数
的不动点是1.(1)已知函数![]() ,求
,求![]() 的不动点.(2)函数
的不动点.(2)函数![]() (
(![]() 是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;(3)已知函数
是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;(3)已知函数![]() (
(![]() ),当
),当![]() 时,若一次函数
时,若一次函数![]() 与二次函数
与二次函数![]() 的交点为
的交点为![]() ,即
,即![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 两点关于直线
两点关于直线![]() 对称,求
对称,求![]() 的取值范围. 22.(10分)某车间加工1200个零件后,采用新工艺,工效提升了20%,这样加工同样多的零件就少用10h,采用新工艺前、后每小时分别加工多少个零件? 23.(12分)某公司招聘职员两名,对甲乙丙丁四名候选人进行笔试和面试,各项成绩均为100分,然后再按笔试70%、面试30%计算候选人综合成绩(满分100分)各项成绩如下表所示:候选人笔试成绩面试成绩甲9088乙8492丙x90丁8886(1)直接写出四名候选人面试成绩中位数;(2)现得知候选人丙的综合成绩为87.2分,求表中x的值;(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要聘请的前两名的人选. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、C4、D5、C6、A7、B8、C9、C10、B11、B12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
的取值范围. 22.(10分)某车间加工1200个零件后,采用新工艺,工效提升了20%,这样加工同样多的零件就少用10h,采用新工艺前、后每小时分别加工多少个零件? 23.(12分)某公司招聘职员两名,对甲乙丙丁四名候选人进行笔试和面试,各项成绩均为100分,然后再按笔试70%、面试30%计算候选人综合成绩(满分100分)各项成绩如下表所示:候选人笔试成绩面试成绩甲9088乙8492丙x90丁8886(1)直接写出四名候选人面试成绩中位数;(2)现得知候选人丙的综合成绩为87.2分,求表中x的值;(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要聘请的前两名的人选. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、C4、D5、C6、A7、B8、C9、C10、B11、B12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、3
14、3![]() 15、
15、![]() 16、017、12或1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)
16、017、12或1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)![]() ;(2)证明见解析.19、(1)见解析;(2)见解析.20、(1)11;(2)1.21、(1
;(2)证明见解析.19、(1)见解析;(2)见解析.20、(1)11;(2)1.21、(1![]() 的不动点为0和2;(2)①
的不动点为0和2;(2)①![]() 时,有唯一的不动点
时,有唯一的不动点![]() ②
②![]() 时,有无数个不动点③
时,有无数个不动点③![]() 时,没有不动点;(3)
时,没有不动点;(3)![]() 的取值范围是
的取值范围是![]() 22、采用新工艺前每时加工20个零件,采用新工艺后每时加工1个零件.23、(1)89分;(2)86;(3)甲的综合成绩: 89.4分,乙的综合成绩: 86.4分,丁的综合成绩为87.4分,以综合成绩排序确定所要招聘的前两名的人选是:甲、丁.
22、采用新工艺前每时加工20个零件,采用新工艺后每时加工1个零件.23、(1)89分;(2)86;(3)甲的综合成绩: 89.4分,乙的综合成绩: 86.4分,丁的综合成绩为87.4分,以综合成绩排序确定所要招聘的前两名的人选是:甲、丁.
相关试卷
这是一份2023-2024学年湖南省株洲市荷塘区第五中学数学九上期末监测模拟试题含答案,共8页。试卷主要包含了已知点等内容,欢迎下载使用。
这是一份湖南省株洲市荷塘区2023-2024学年八上数学期末达标检测模拟试题含答案,共7页。
这是一份2023年湖南省株洲市荷塘区中考二模数学试题(含答案),共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。








