

滨州市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案
展开这是一份滨州市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案,共6页。试卷主要包含了在平面直角坐标系中,点M,当x=1时,下列式子无意义的是,若化简的结果为,则的取值范围是,下面几种说法等内容,欢迎下载使用。
滨州市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某天小明骑自行车上学,途中因自行车发生故障,修车耽误一段时间后继续骑行,按时赶到了学校.如图描述了他上学情景,下列说法中错误的是( )
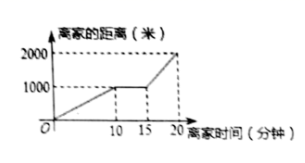
A.用了5分钟来修车 B.自行车发生故障时离家距离为1000米
C.学校离家的距离为2000米 D.到达学校时骑行时间为20分钟
2.下图入口处进入,最后到达的是( )

A.甲 B.乙 C.丙 D.丁
3.在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.关于一元二次方程![]() 根的情况描述正确的是( )
根的情况描述正确的是( )
A.有两个相等的实数根 B.没有实数根
C.有两个不相等的实数根 D.不能确定
5.下列图形中的曲线不表示y是x的函数的是( )
A. B.
B.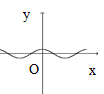 C.
C.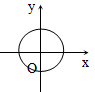 D.
D.
6.当x=1时,下列式子无意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若化简![]() 的结果为
的结果为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.一切实数 B.![]() C.
C.![]() D.
D.![]()
8.下面几种说法:①对角线互相垂直的四边形是菱形;②一组对边平行,一组邻边相等的四边形是菱形;③对角线相等的平行四边形是矩形;④对角线互相垂直平分的四边形是菱形,那么准确的说法是( )
A.①②③ B.②③ C.③④ D.②④
9.人文书店三月份销售某畅销书100册,五月份销售量达196册,设月平均增长率为x,则可列方程( )
A.100(1+x)=196![]() B.100(1+2x)=196
B.100(1+2x)=196
C.100(1+x2)=196 D.100(1+x)2=196
10.已知三角形的三边为2、3、4,该三角形的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.一个不透明的袋子中装有21个红球和若干个白球,这些球除了颜色外都相同,若小英每次从袋子中随机摸出一个球,记下颜色后再放回,经过多次重复试验,小英发现摸到红球的频率逐渐稳定于1.4,则小英估计袋子中白球的个数约为( )
A.51 B.31 C.12 D.8
12.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
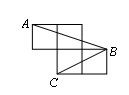
A.90° B.60° C.45° D.30°
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.当![]() 时,二次根式
时,二次根式![]() 的值是___________.
的值是___________.
14.若式子![]() 有意义,则x的取值范围为___________.
有意义,则x的取值范围为___________.
15.如图,在![]() 中,
中,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,则
,则![]() __________
__________![]() .
.

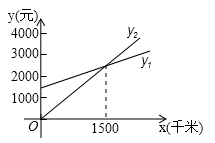
16.如图,某公司准备和一个体车主或一民营出租车公司中的一家签订月租车合同,设汽车每月行驶,个体车主收费为![]() 元,民营出租车公司收费为
元,民营出租车公司收费为![]() 元,观察图像可知,当
元,观察图像可知,当![]() _________
_________![]() 时,选用个体车主较合算.
时,选用个体车主较合算.
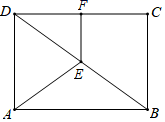
17.如图,BD是矩形ABCD的一条对角线,点E,F分别是BD,DC的中点.若AB=4,BC=3,则AE+EF的长为_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)为调查某校初二学生一天零花钱的情况,随机调查了初二级部分学生的零钱金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
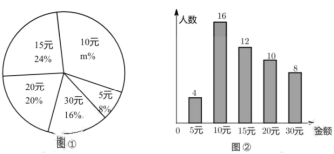
(1)本次接受随机抽样调查的学生人数为_____,图①中![]() 的值是_____;
的值是_____;
(2)求本次调查获取的样本数据的平均数;
(3)根据样本数据,估计该年级300名学生每天零花钱不多于10元的学生人数.
19.(5分)如图1.点D,E在△ABC的边BC上.连接AD.AE.①AB=AC:②AD=AE:
③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论.构成三个命题:①②![]() ③;①③
③;①③![]() ②,②③
②,②③![]() ①.
①.
(1)以上三个命题是真命题的为(直接作答)__________________;
(2)选择一个真命题进行证明(先写出所选命题.然后证明).
20.(8分)某移动通信公司推出了如下两种移动电话计费方式.
| 月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) |
方式一 |
|
|
|
方式二 |
|
|
|
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费![]() 元,当主叫计时不超过
元,当主叫计时不超过![]() 分钟不再额外收费,超过
分钟不再额外收费,超过![]() 分钟时,超过部分每分钟加收
分钟时,超过部分每分钟加收![]() 元(不足
元(不足![]() 分钟按
分钟按![]() 分钟计算).
分钟计算).
(1)请根据题意完成如表的填空:
| 月主叫时间 | 月主叫时间 |
方式一收费/元 | ______________ |
|
方式二收费/元 |
| _______________ |
(2)设某月主叫时间为![]() (分钟),方式一、方式二两种计费方式的费用分别为
(分钟),方式一、方式二两种计费方式的费用分别为![]() (元),
(元),![]() (元),分别写出两种计费方式中主叫时间
(元),分别写出两种计费方式中主叫时间![]() (分钟)与费用为
(分钟)与费用为![]() (元),
(元),![]() (元)的函数关系式;
(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.
21.(10分)(1)计算:![]()
(1)化简求值:![]() ,其中x=1.
,其中x=1.
22.(10分)如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
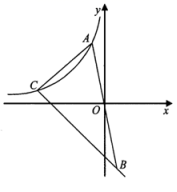
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
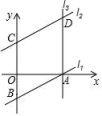
23.(12分)如图,直线l1交x轴于A(3,0),交y轴于B(0,﹣2)
(1)求直线l1的表达式;
(2)将l1向上平移到C(0,3),得到直线l2,写出l2的表达式;
(3)过点A作直线l3⊥x轴,交l2于点D,求四边形ABCD的面积.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、B
4、A
5、C
6、C
7、B
8、C
9、D
10、D
11、B
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、2
14、x≥5
15、1
16、![]()
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)50,32;(2)16;(3)1.
19、(1)①②![]() ③;①③
③;①③![]() ②;②③
②;②③![]() ①. (2)见解析
①. (2)见解析
20、(1)![]() ,
,![]() ;(2)
;(2)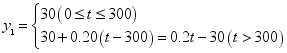 ,
,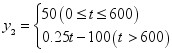 ;(3)当
;(3)当![]() 时方式一省钱;当
时方式一省钱;当![]() 时,方式二省钱,当
时,方式二省钱,当![]() 时;方式一省钱,当为
时;方式一省钱,当为![]() 分钟、
分钟、![]() 分钟时,两种方式费用相同
分钟时,两种方式费用相同
21、(1)3;(1)![]() ,
,![]() .
.
22、(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
23、(1)直线l1的表达式为:y=![]() x﹣2;(2)直线l2的表达式为:y=
x﹣2;(2)直线l2的表达式为:y=![]() x+3;(3)四边形ABCD的面积=1.
x+3;(3)四边形ABCD的面积=1.
相关试卷
这是一份漯河市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份洛阳市重点中学2022-2023学年数学七年级第二学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了化简的结果是等内容,欢迎下载使用。
这是一份2022-2023学年雅安市重点中学数学七年级第二学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,已知直线y=mx+n,函数y=中自变量x的取值范围为等内容,欢迎下载使用。












